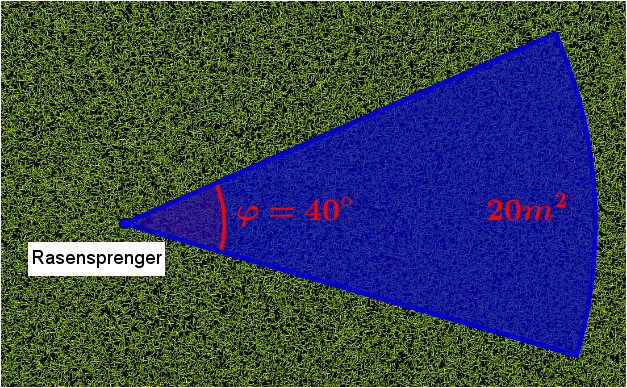
Der abgebildete Rasensprenger schwenkt um 40° und besprüht so eine Rasenfläche von .
Wie groß ist seine Reichweite?
Gib das Ergebnis auf zwei Stellen nach dem Komma gerundet ein.

Quelle: Sebastian & Kari, CC BY-SA 2.0, Wikimedia Commons
m
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?