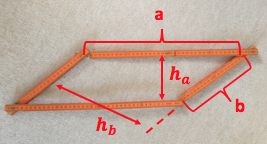
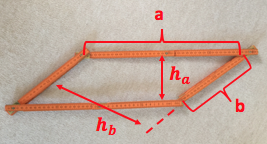
Experimentiere mit einem Zollstock
Mit einem Zollstock lassen sich leicht verschiedene Parallelogramme formen.

Durch die Seitenlängen (und somit auch durch seinen "Umfang", d.h. die Summe der Seitenlängen) ist die Form eines Parallelogramms nicht bestimmt. Zeige dies!
Welche Form besitzt ein Parallelogramm mit vorgegebenen Seitenlängen, wenn seine beiden Höhen am größten sind?
Was passiert mit der Höhe eines bestimmten "Zollstockparallelogramms", wenn man dieses ohne Veränderung der Seitenlängen so verbiegt, dass die Höhe nur noch die Hälfte (den dritten Teil; den vierten Teil) beträgt?
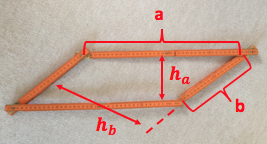
Wahr oder falsch?
Wird ohne Veränderung der Seitenlängen eine Höhe eines Parallelogramms um (, ) kleiner, dann wird auch die andere Höhe um (, ) kleiner.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?