Parallelogramme lassen sich mit anderen Vierecken zu vielfältigen Formen zusammensetzen.
Berechne die Flächeninhalte der angegebenen Buchstaben-Formen.
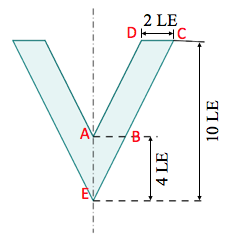
Berechne die gezeichnete Fläche.
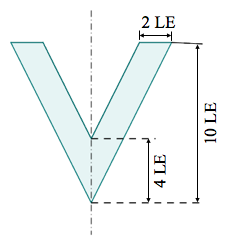 cm²
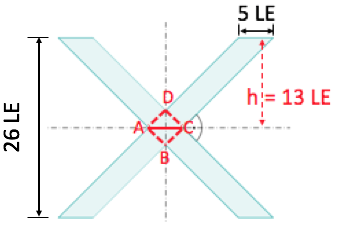
cm²Berechne die gezeichnete Fläche.
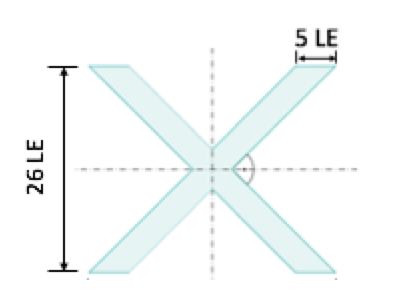 FE
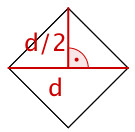
FEBerechne die gezeichnete Fläche.
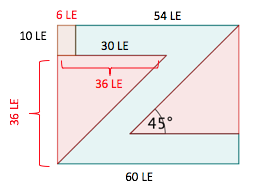
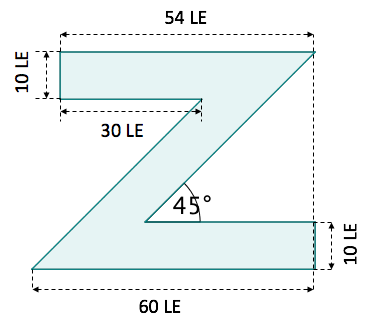 FE
FE
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?