Meetingpoints am Trapez
Wie bei anderen Vierecken sind auch beim Trapez der Schnittpunkt der Diagonalen und der Schwerpunkt von besonderer Bedeutung.

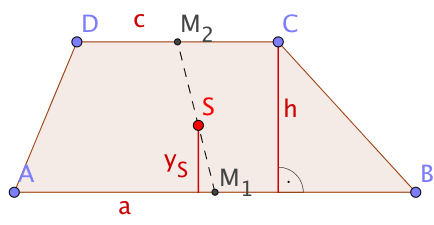
Im Trapez mit den Grundseiten und und der Höhe sei der Schnittpunkt der Diagonalen und der Schwerpunkt des Trapezes.
Der Schwerpunkt eines Trapezes liegt auf der Verbindungstrecke der Mittelpunkte der Grundseiten (Mittenlinie) und hat von der Grundseite den Abstand
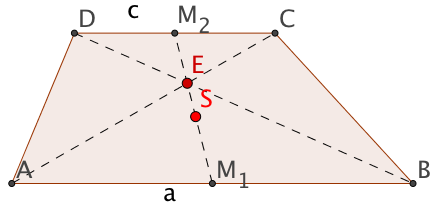
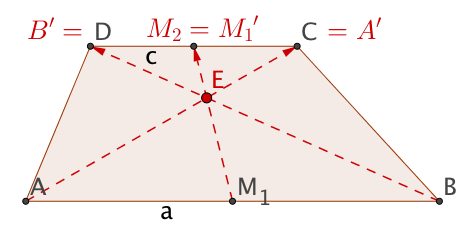
Beweise, dass die Mittenlinie eines jeden Trapezes durch den Schnittpunkt der Diagonalen geht.
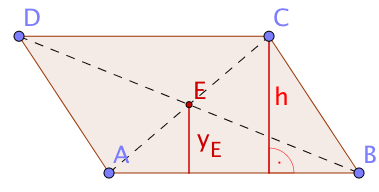
Begründe, dass der Schwerpunkt und der Diagonlenschnittpunkt zusammenfallen, wenn das Trapez zu einem Parallelogramm wird.
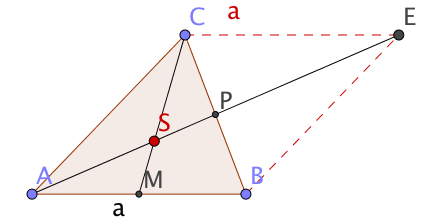
So konstruiert man den Schwerpunkt eines Trapezes:
Zeichne die Mittenlinie des Trapezes.
Verlängere über hinaus um die Strecke zum Endpunkt .
Verlängere über hinaus um die Strecke zum Endpunkt .
Der Schnittpunkt von mit ist der Schwerpunkt .
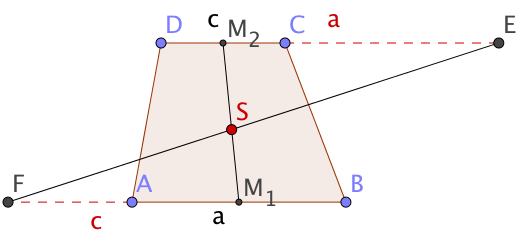
Begründe, warum für mit dieser Konstruktion der Schwerpunkt eines Dreiecks konstruiert wird.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?