Aufgaben zum Thema Winkel
Wie gut kennst du dich aus? Mit diesen gemischten Übungsaufgaben lernst du, Winkel zu erkennen und zu messen.
- 1
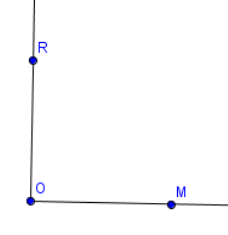
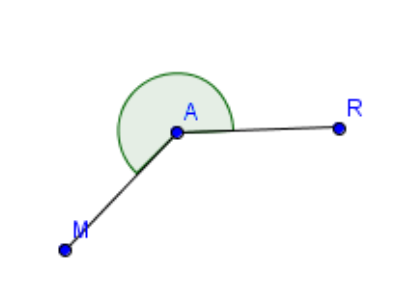
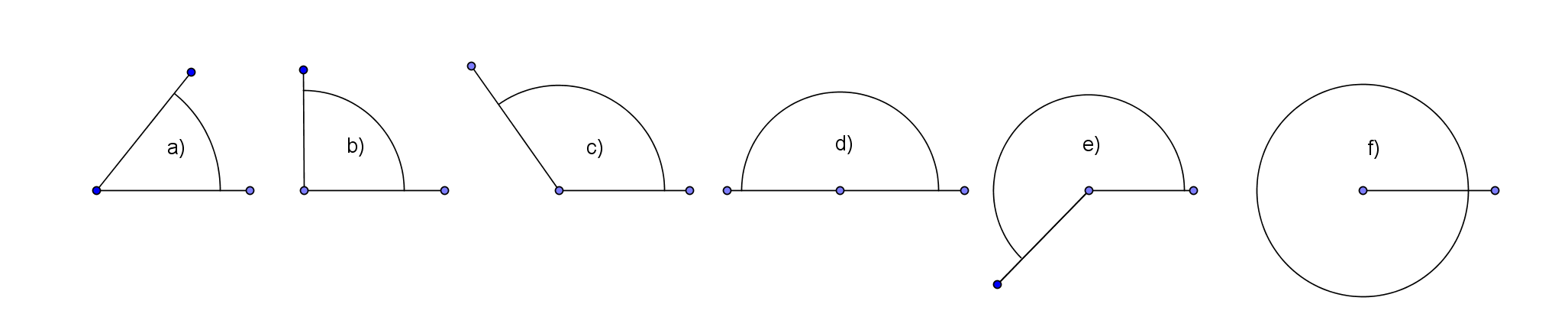
Gib jeweils an, um welche Winkelart es sich handelt. Klicke auf das Bild, um es größer angezeigt zu bekommen.
- 2
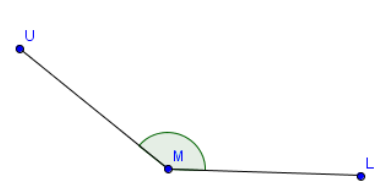
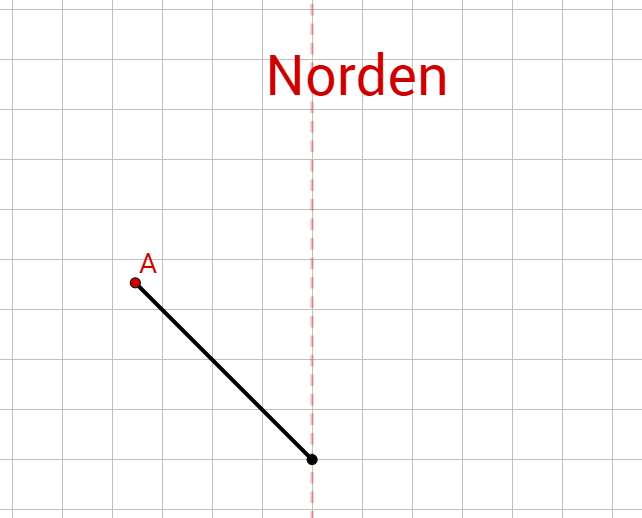
Miss folgenden Winkel und bezeichne ihn mit den Punkten
- 3
Zeichne die folgenden Winkel
- 4
Zeichne mit dem Geodreieck einen Winkel von , dessen offene Seite nach rechts zeigt, und einen Winkel von , dessen offene Seite nach links zeigt. Was fällt dir auf?
- 5
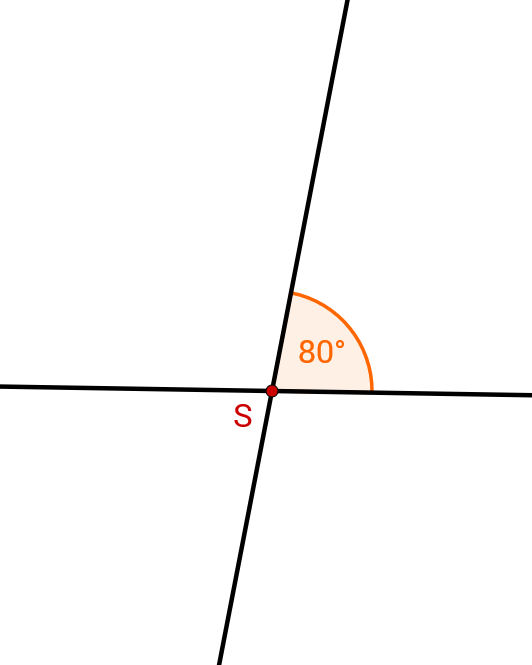
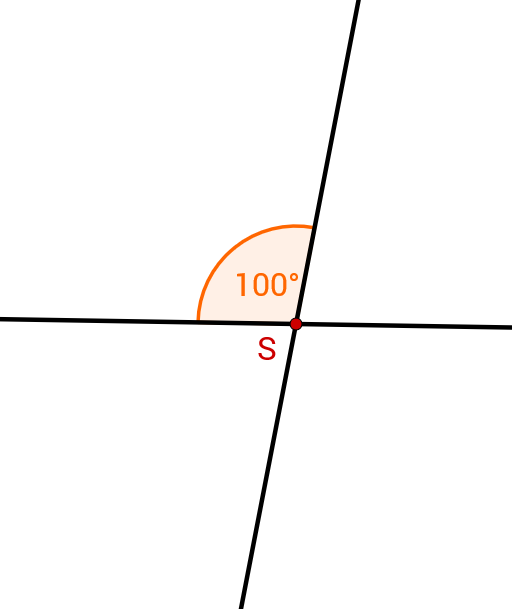
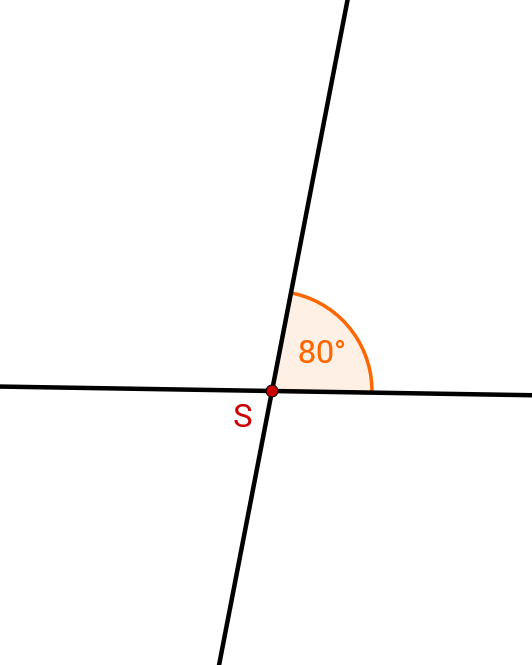
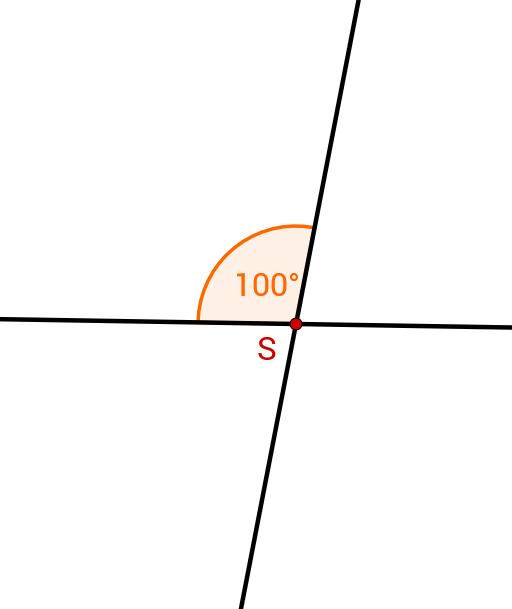
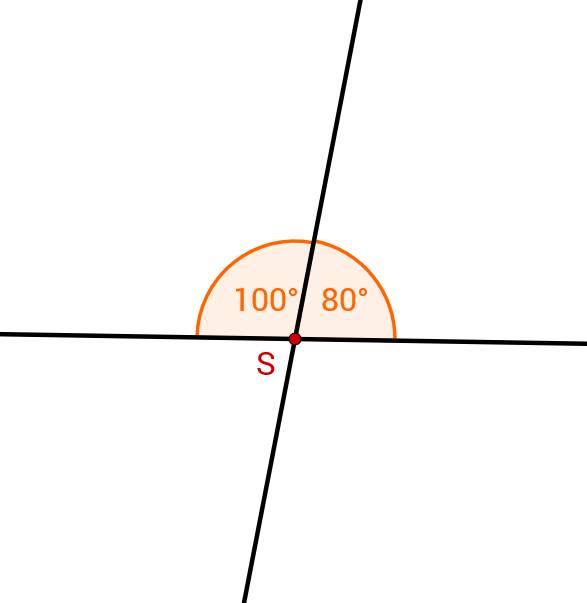
Betrachte die nachfolgende Abbildung. Es gilt: .
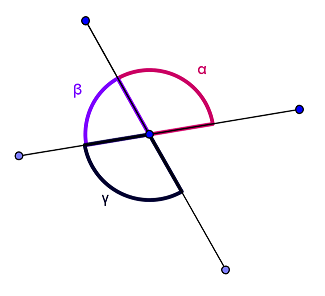
Bestimme die Größe des Winkels .
Gib nur die Masszahl ohne das Grad-Zeichen ein.
°Bestimme die Größe des Winkels .
Gib nur die Masszahl ohne das Grad-Zeichen ein.
°
- 6
Berechne durch Umwandlung in Winkelminuten und Winkelsekunden:
- 7
Bearbeite folgende Teilaufgaben:
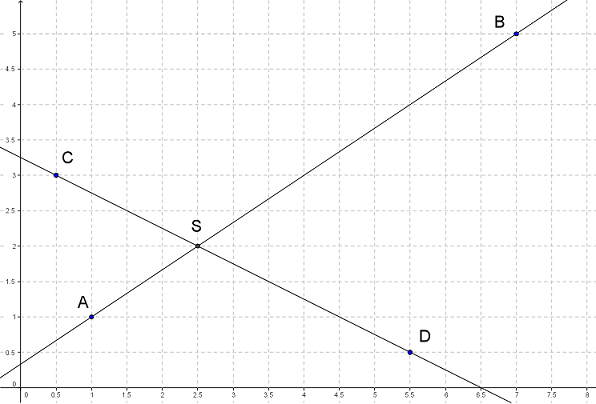
Trage die Punkte A(1|1), B(7|5), C(0,5|3) und D(5,5|0,5) und die Geraden AB und CD in das Koordinatensystem ein. Bezeichne den Schnittpunkt der beiden Geraden mit S.
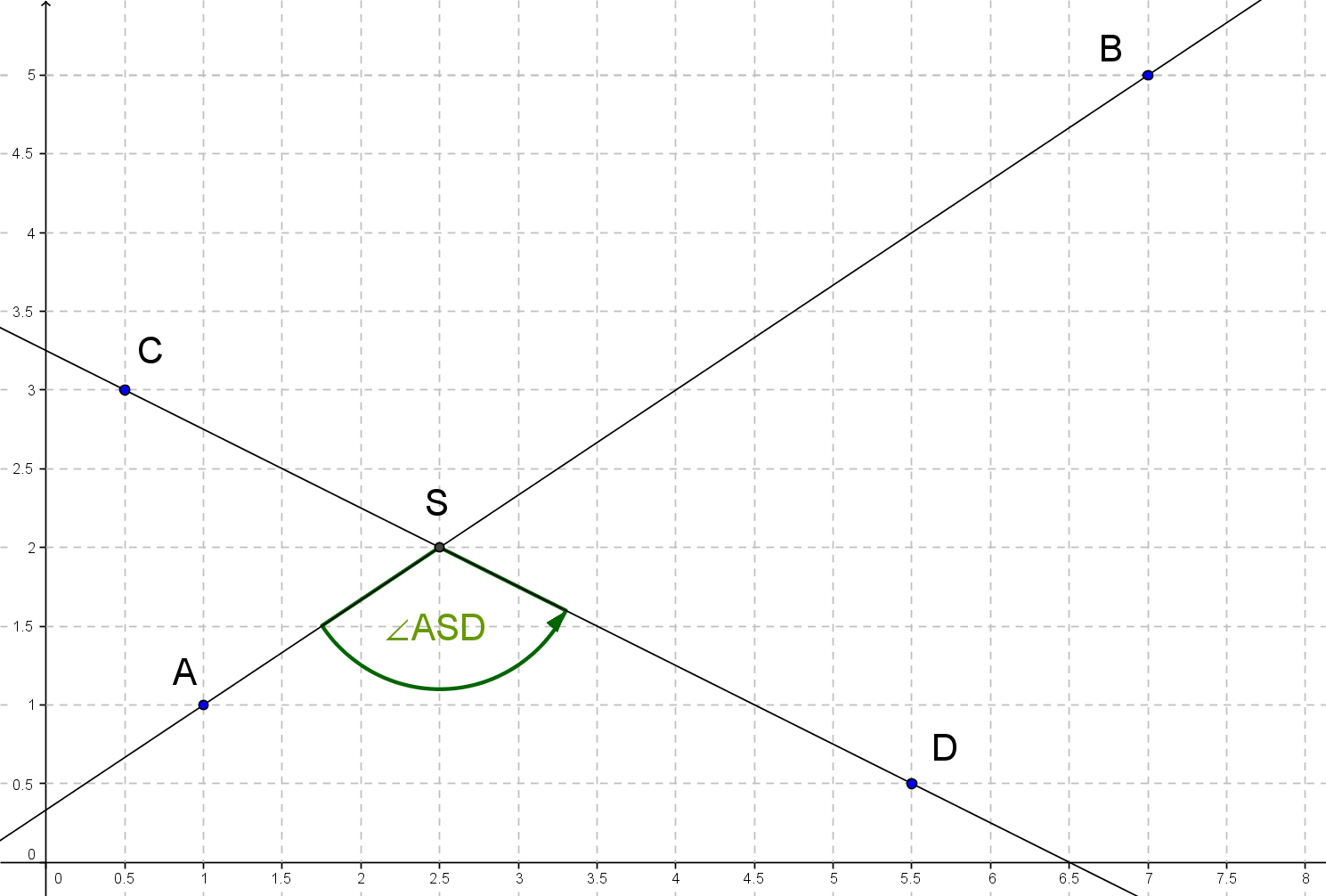
Kennzeichne den Winkelbogen von mit grüner Farbe, so dass auch seine Orientierung deutlich wird.
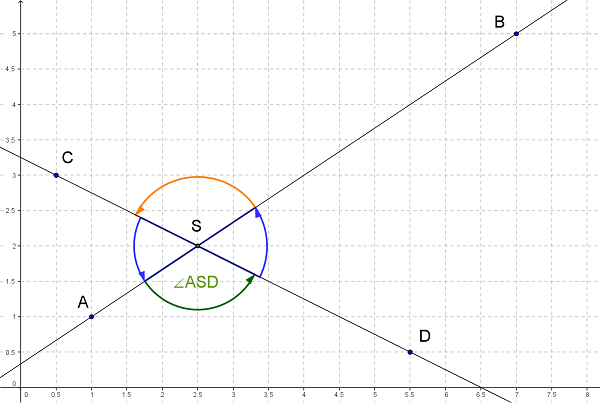
Zeichne den Scheitelwinkel zu mit oranger Farbe und die beiden Nebenwinkel mit blauer Farbe.
Miss den Winkel und gib seine Winkelart an!
- 8
Berechne, welchen stumpfen Winkel die Zeiger einer Uhr um 14.32 Uhr einschließen.
° - 9
Winkel an der Uhr: Es ist 4 Uhr.
Welches Winkelmaß schließen Stunden- und Minutenzeiger ein?
°Welchen Bruchteil eines Vollwinkels stellt dar?
Welches Winkelmaß überstreicht der Minutenzeiger in 11 Minuten?
°
- 10
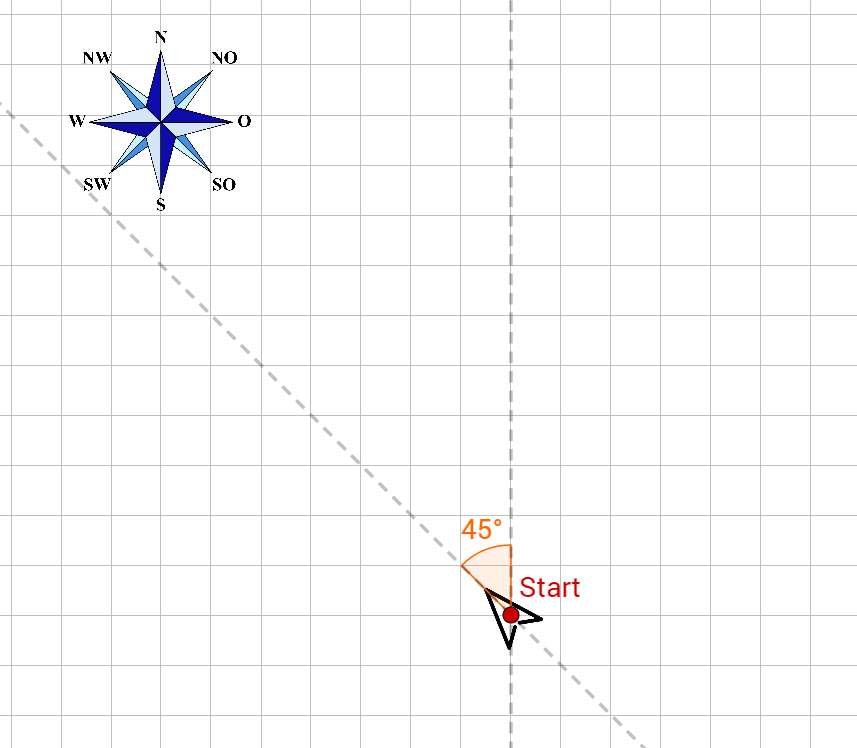
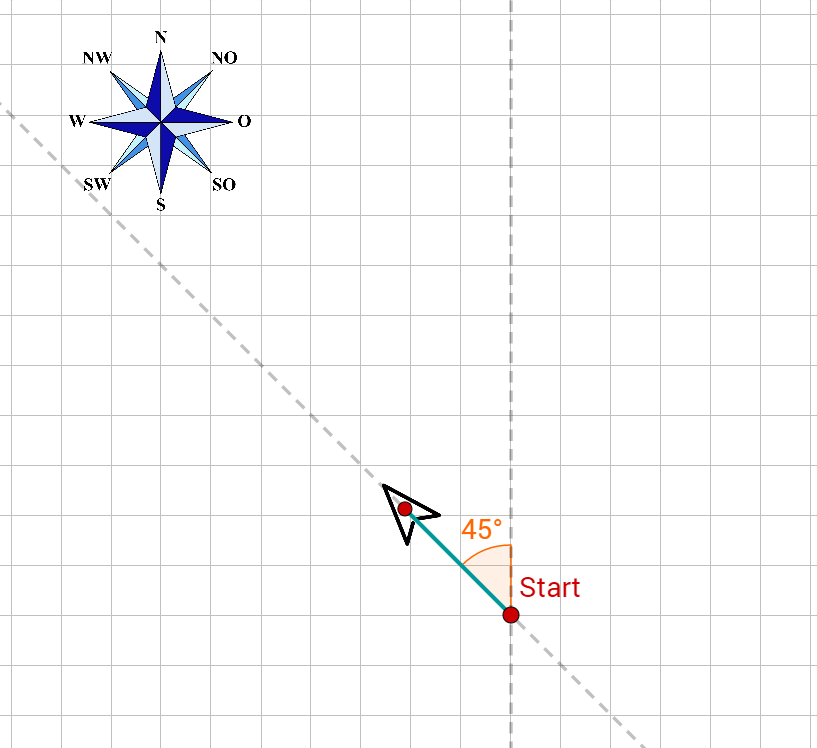
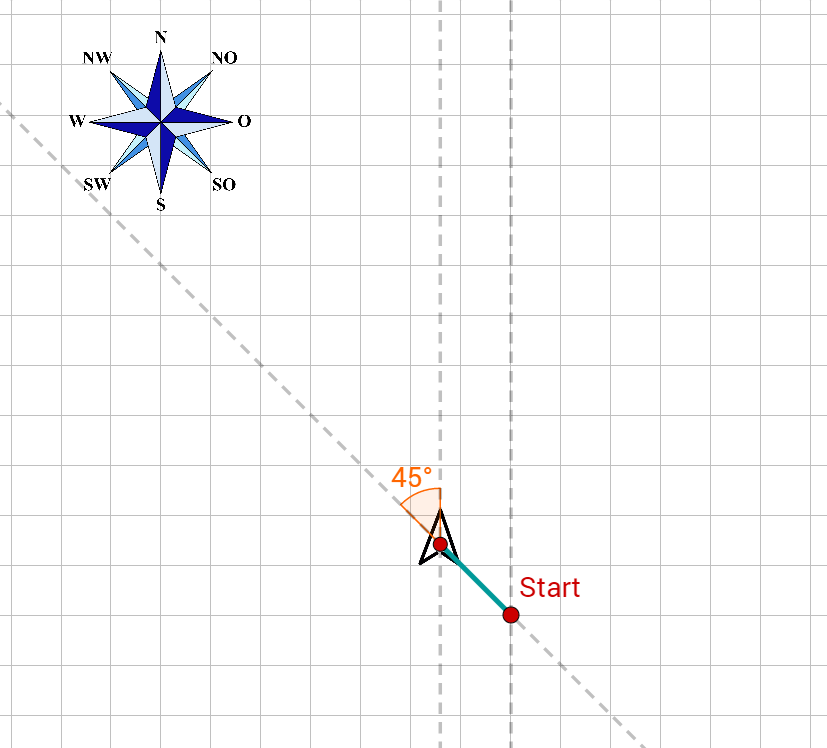
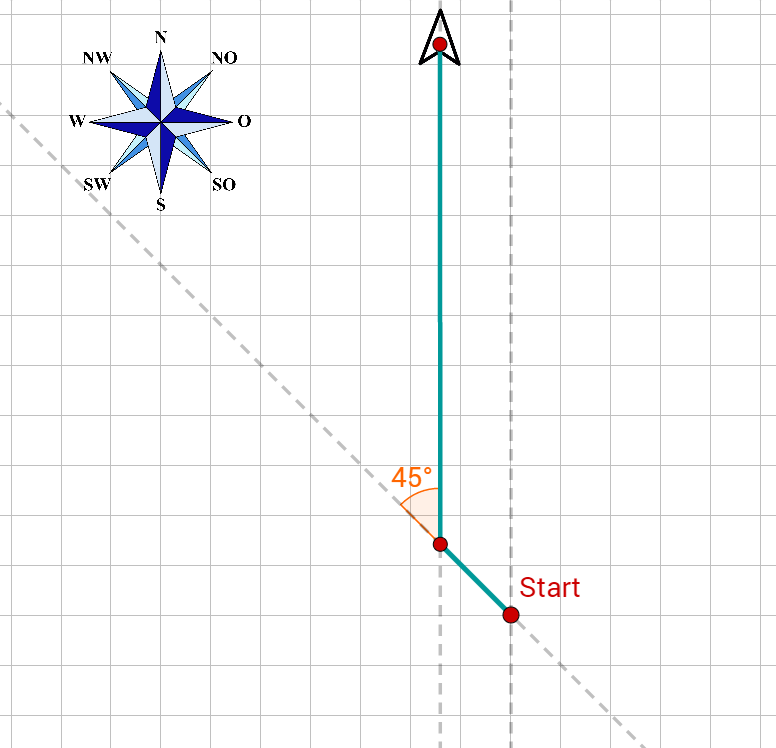
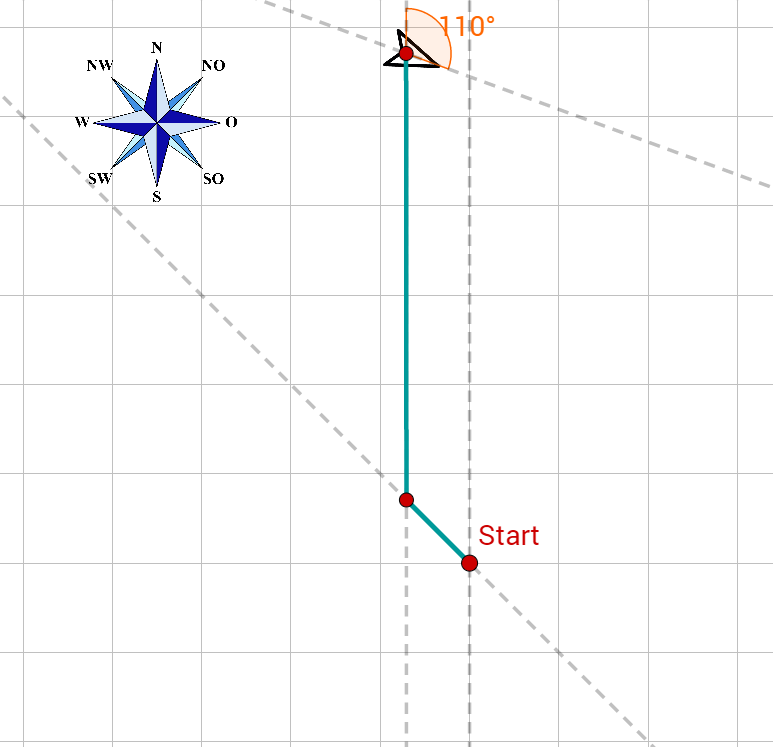
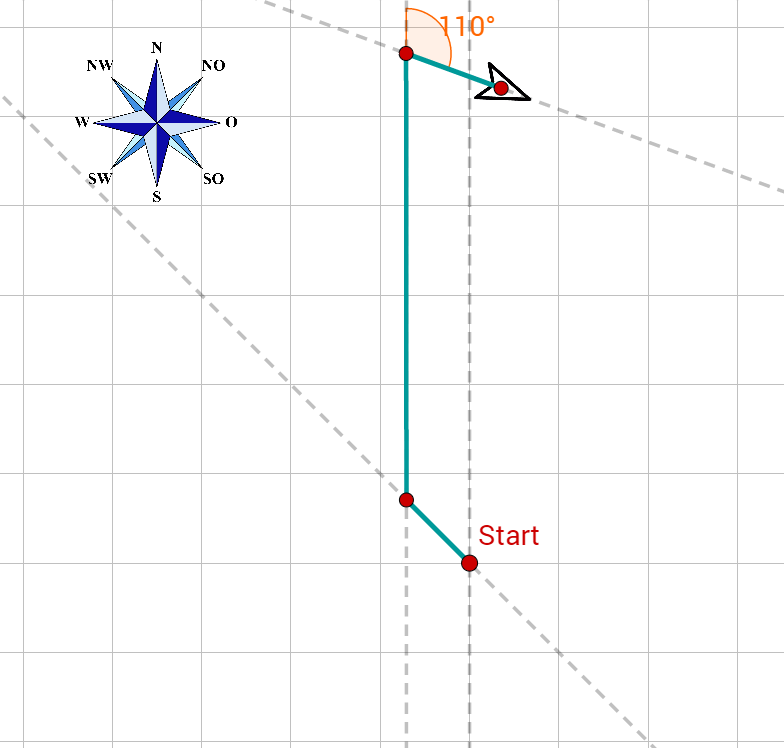
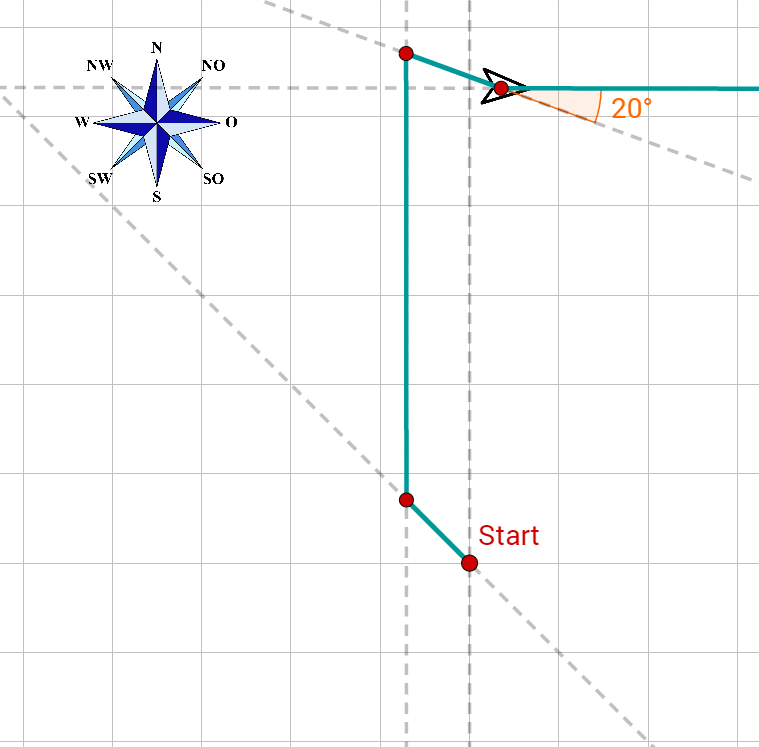
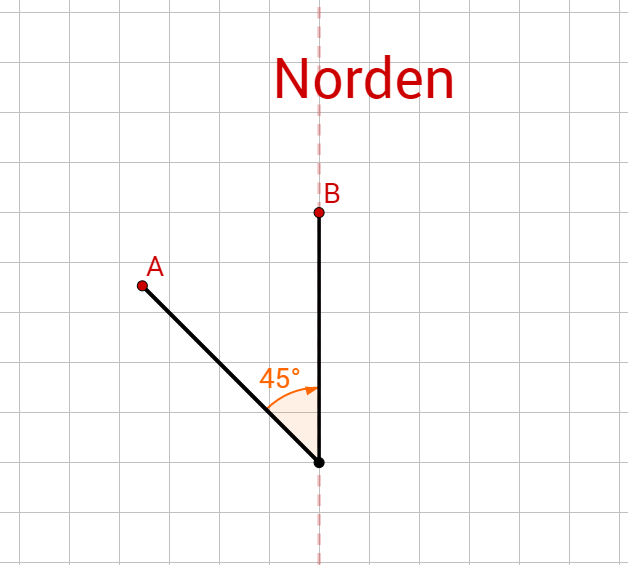
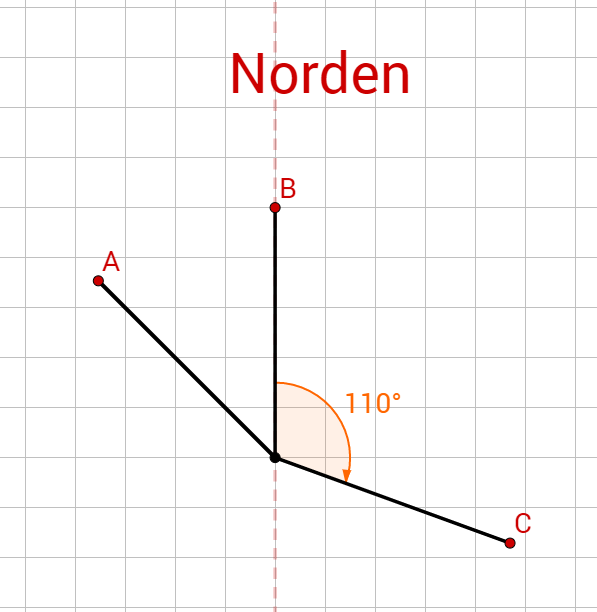
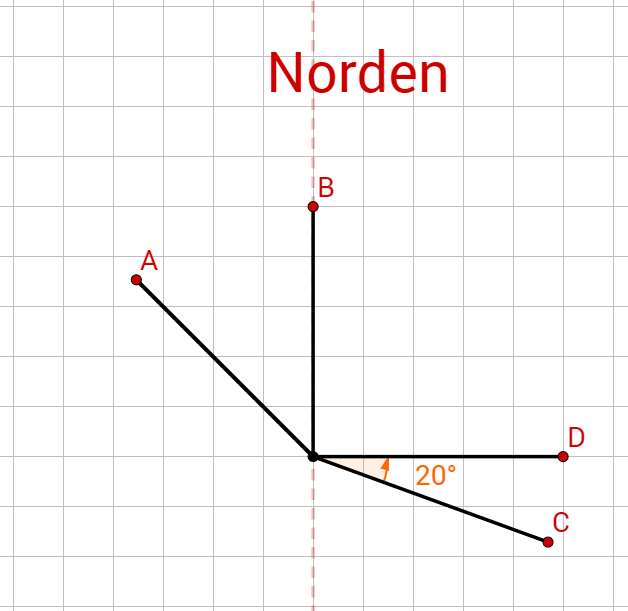
Ein Schiff fährt zunächst 10 km nach Nordwesten, dreht dann um 45° Richtung N, dann nach 50 km um 110° im Uhrzeigersinn und schließlich nach weiteren 10 km um 20° gegen den Uhrzeigersinn. Um wie viel hat sich das Schiff insgesamt gedreht? In welche Richtung? In welche Richtung (gemessen in Grad gegenüber der Nordrichtung) fährt es jetzt?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?