Aufgaben zur Pyramide
Hier findest du Aufgaben zu Pyramiden. Übe, deren Volumen und Kantenlängen zu berechnen.
- 1
Die Cheops-Pyramide hat ungefähr die Länge 230m, die Breite 230m und die Höhe 139m. Wie groß ist ihr Volumen?
 m³
m³ - 2
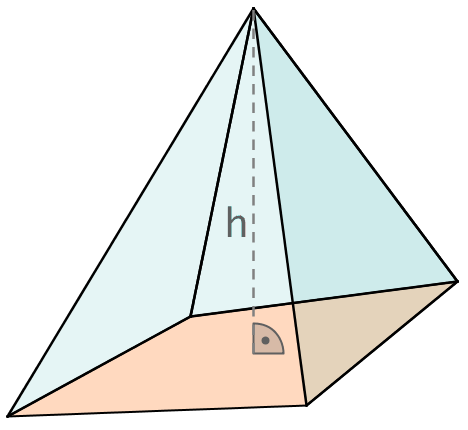
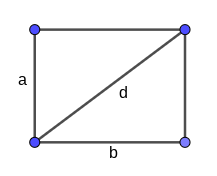
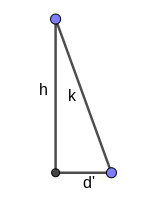
Gegeben ist eine gerade Pyramide. Die Grundfläche der Pyramide ist ein Rechteck mit den Seitenlängen und . Die Höhe der Pyramide beträgt .
Berechne das Volumen und die Kantenlänge der Pyramide.
- 3
Eine Pyramide hat eine dreieckige Grundfläche. Die Grundseite des Dreiecks hat eine Länge von und die dazugehörige Höhe beträgt . Die Pyramide besitzt eine Höhe . Berechne das Volumen der Pyramide.
cm³ - 4
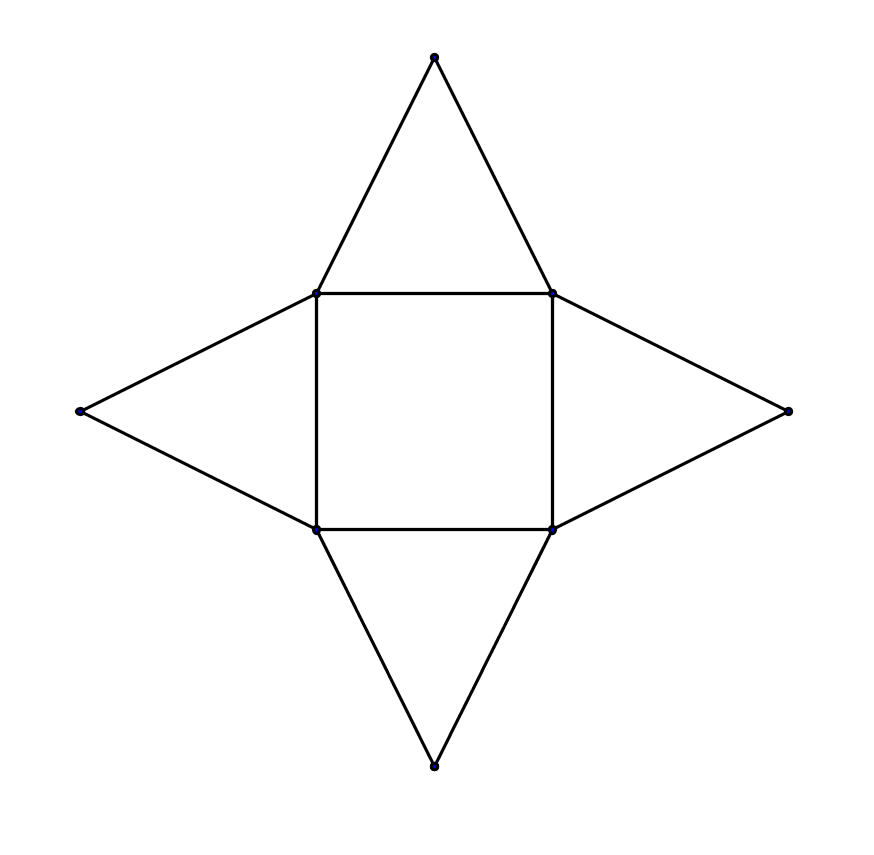
Konstruiere das Netz einer geraden quadratischen Pyramide mit einer Grundkantenlänge und einer Seitenkantenlänge . Baue anschließend ein Papiermodell dieser Pyramide.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?