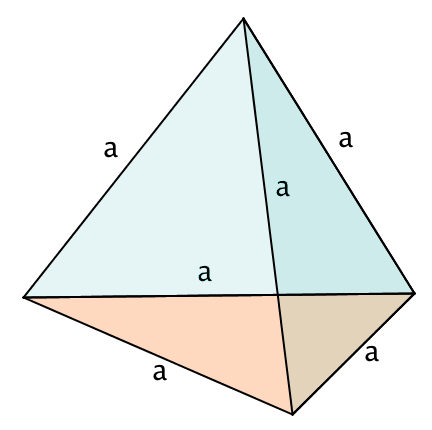
Ein reguläres Tetraeder (Tetraeder = dreiseitige Pyramide) ist eine Pyramide, die
vier kongruente gleichseitige Dreiecke als Fläche hat,
sechs gleich lange Kanten hat.
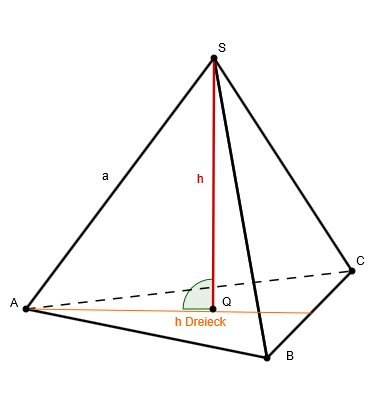
Höhe eines Tetraeders
Volumen eines Tetraeders

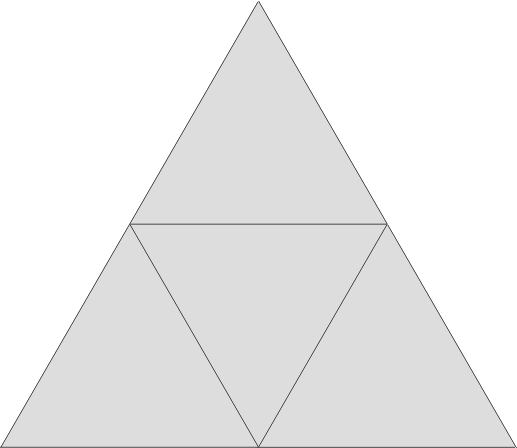
Oberflächeninhalt eines Tetraeders
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
