Aufgaben zum Volumen eines Zylinders
Teste dein Wissen zu Zylindern mit diesen gemischten Übungsaufgaben! Lerne, das Volumen eines Zylinders zu bestimmen.
- 1
Der Durchmesser des Mülleimers ist 30 cm und die Höhe ist 60 cm (ohne den Deckel). Wie groß ist das Volumen?
Runde auf ganze .
 cm³
cm³ - 2
Ein zylindrisches Ausdehnungsgefäß hat d=35cm Durchmesser und h=450mm Höhe.
Wie viel Liter fasst das Gefäß?
- 3

Dieses Glas hat einen Durchmesser von 7 cm und seine Höhe ist 8 cm.
Berechne das Volumen des Glases. Runde dein Ergebnis auf Einer.
- 4

In ein Glas mit dem Innendurchmesser 8 cm werden 150 ml Wasser eingegossen.
Wie viele cm steht das Wasser im Glas? Runde auf ganze Zahlen.
- 5
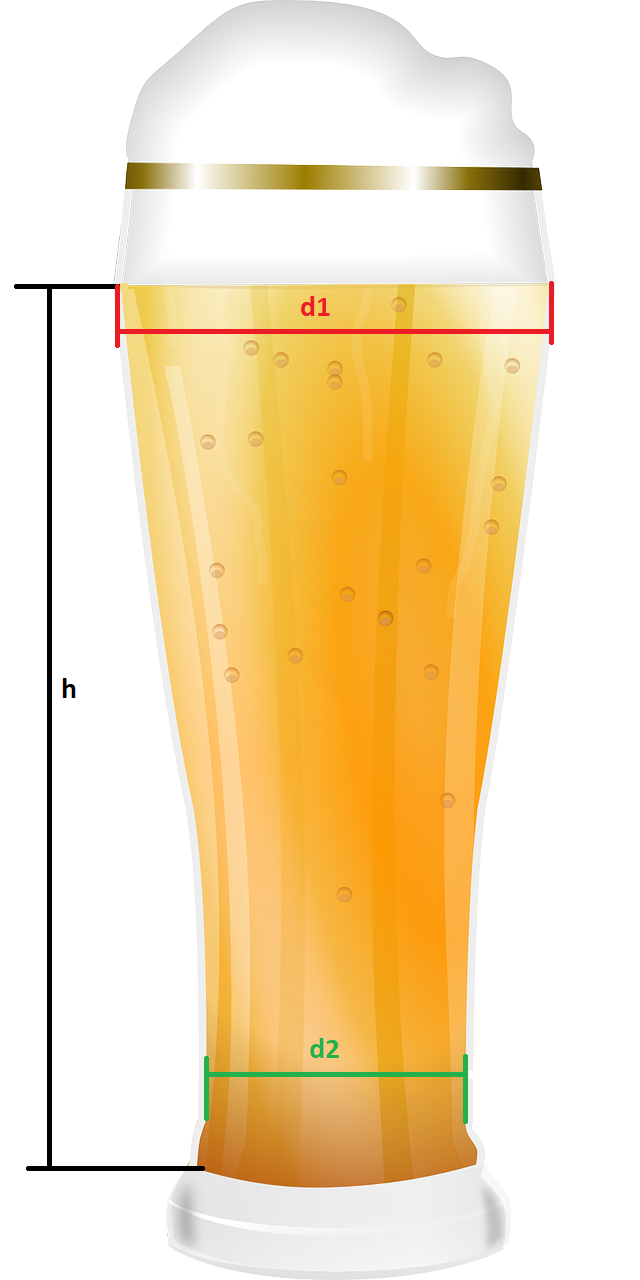
Ein Weißbierglas hat bis zur Eichmarkierung eine Füllhöhe von . Außerdem hat es den maximalen Durchmesser und den minimalen Durchmesser .
Schätze mit diesen Zahlen das wahre Volumen des Gefäßinhaltes nach oben und nach unten ab.
- 6
Eine Toilettenpapierrolle besteht aus dem Toilettenpapier und einer zylinderförmigen Rolle aus Karton.
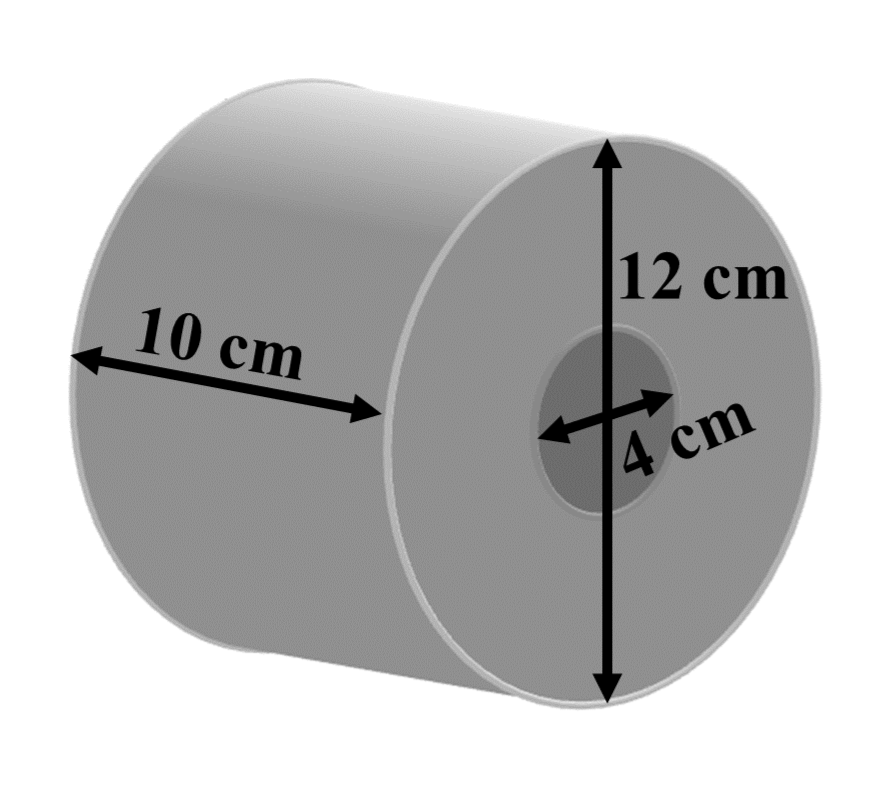
Das Toilettenpapier hat eine Breite von .
Der Durchmesser der zylinderförmigen Rolle sind .
Der Gesamtdurchmesser der Toilettenpapierrolle beträgt .
Berechne das Volumen des Toilettenpapiers.
- 7

Ein Goldschmied möchte einen Ring designen.
Der Innendurchmesser des Rings soll betragen, der Außendurchmesser .
Der Ring soll außerdem breit sein.
Der Goldschmied möchte den Ring mit Silber herstellen. Silber hat eine Dichte von pro Kubikzentimeter.
Berechne zuerst das Volumen des Rings in Kubikzentimeter und runde auf zwei Nachkommastellen.
Bestimme, wie viel Gramm Silber der Goldschmied benötigt, um den Ring zu schmieden.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
