In dieser Aufgabe geht es darum, zu berechnen.
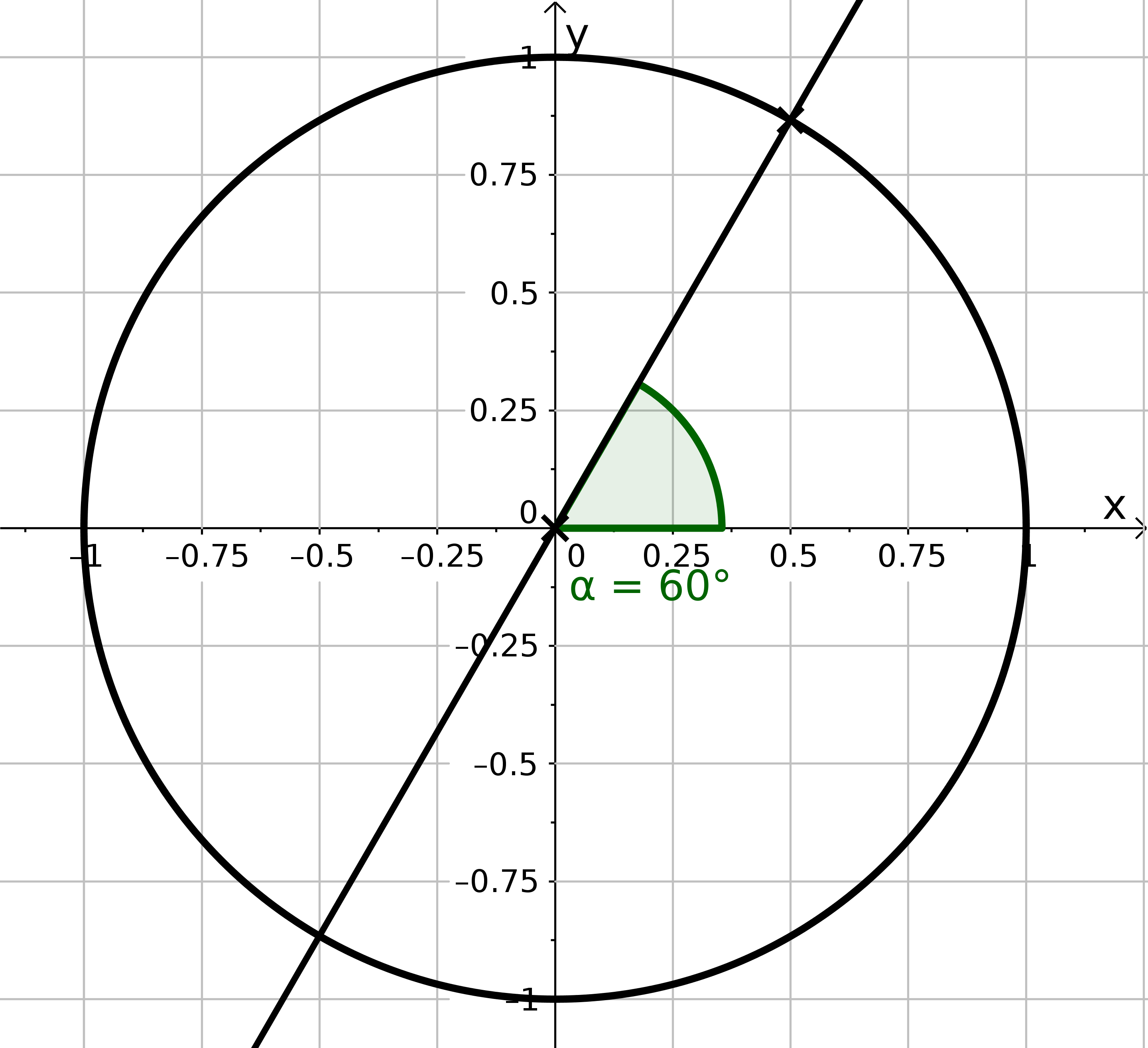
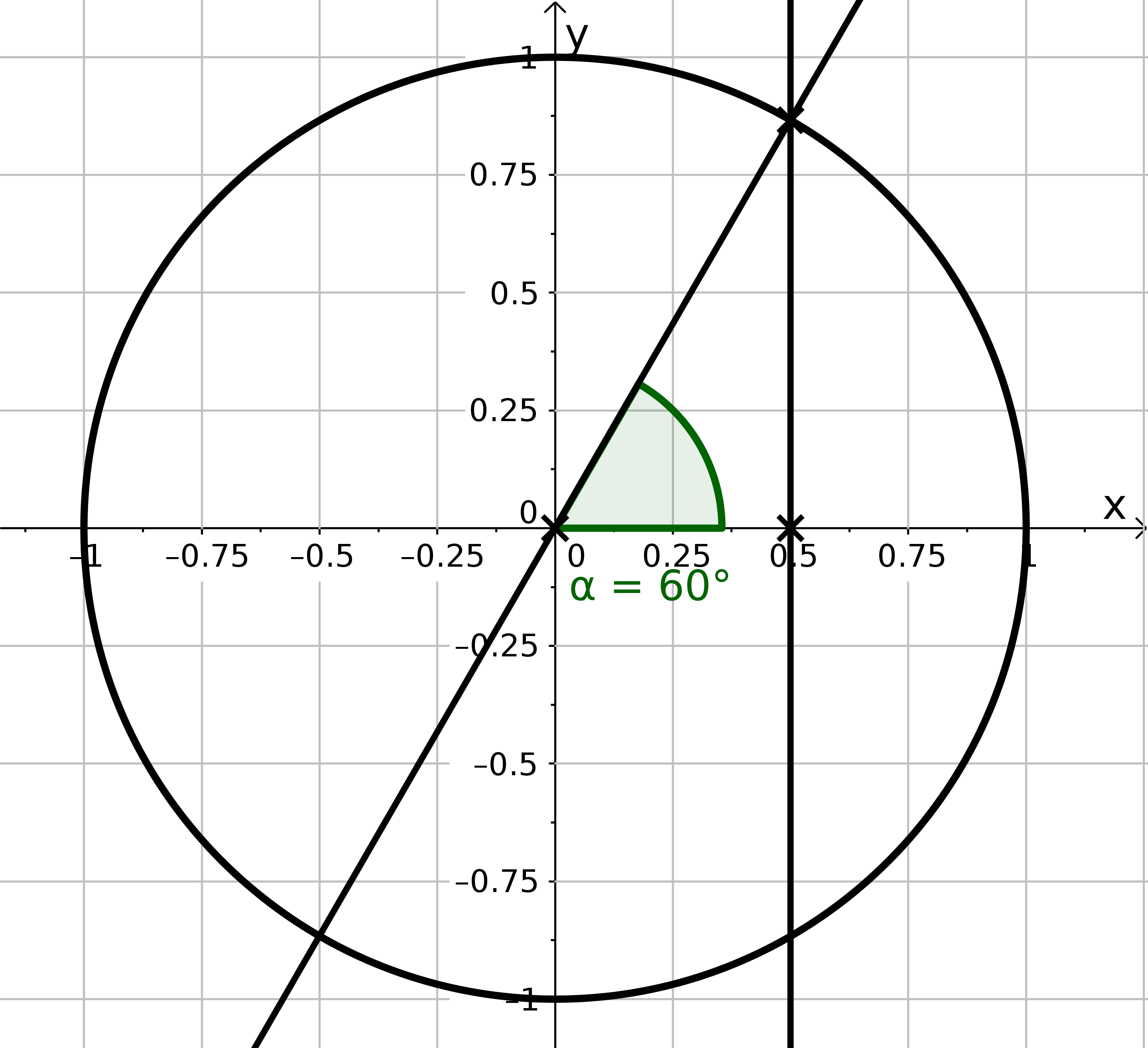
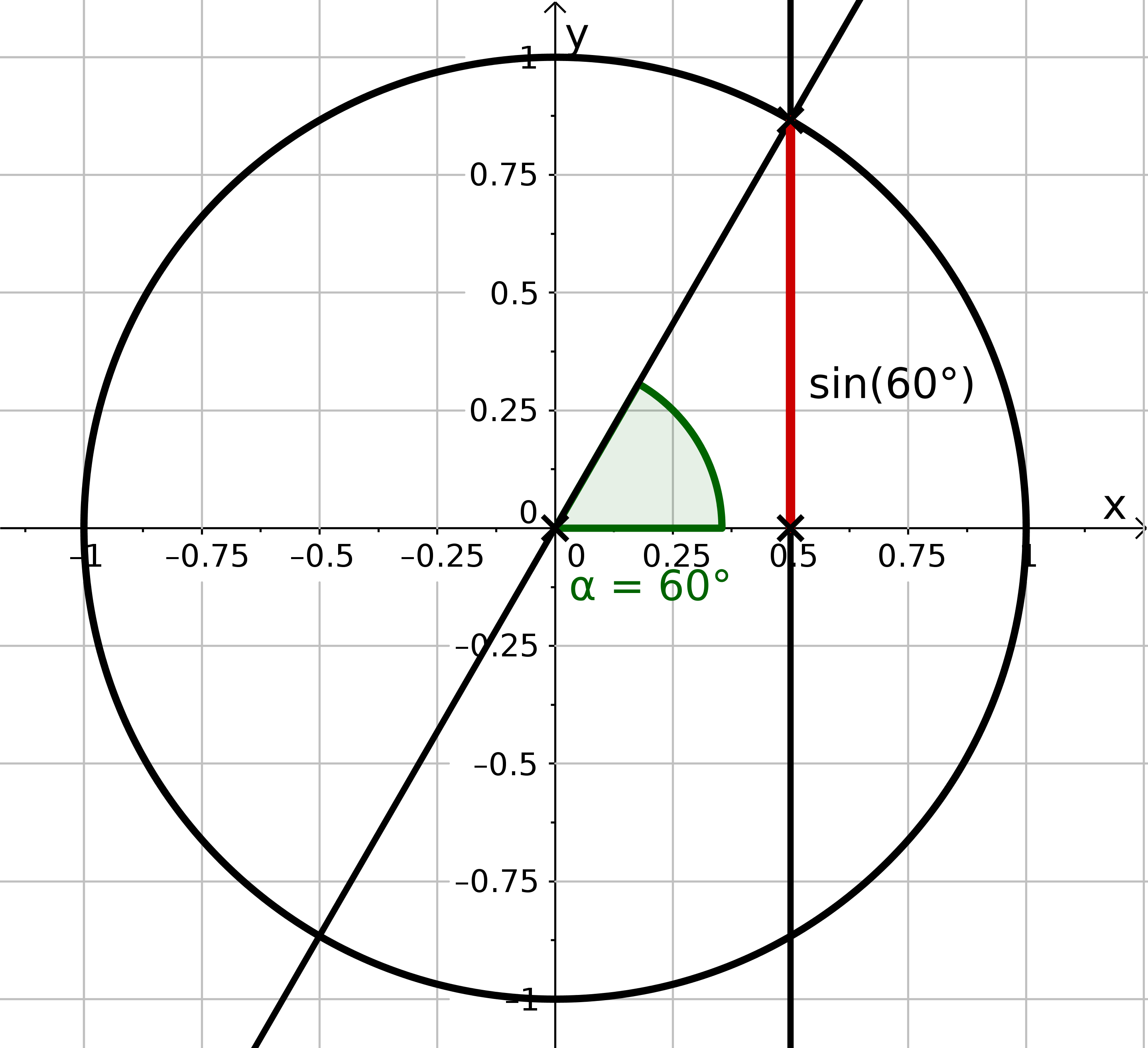
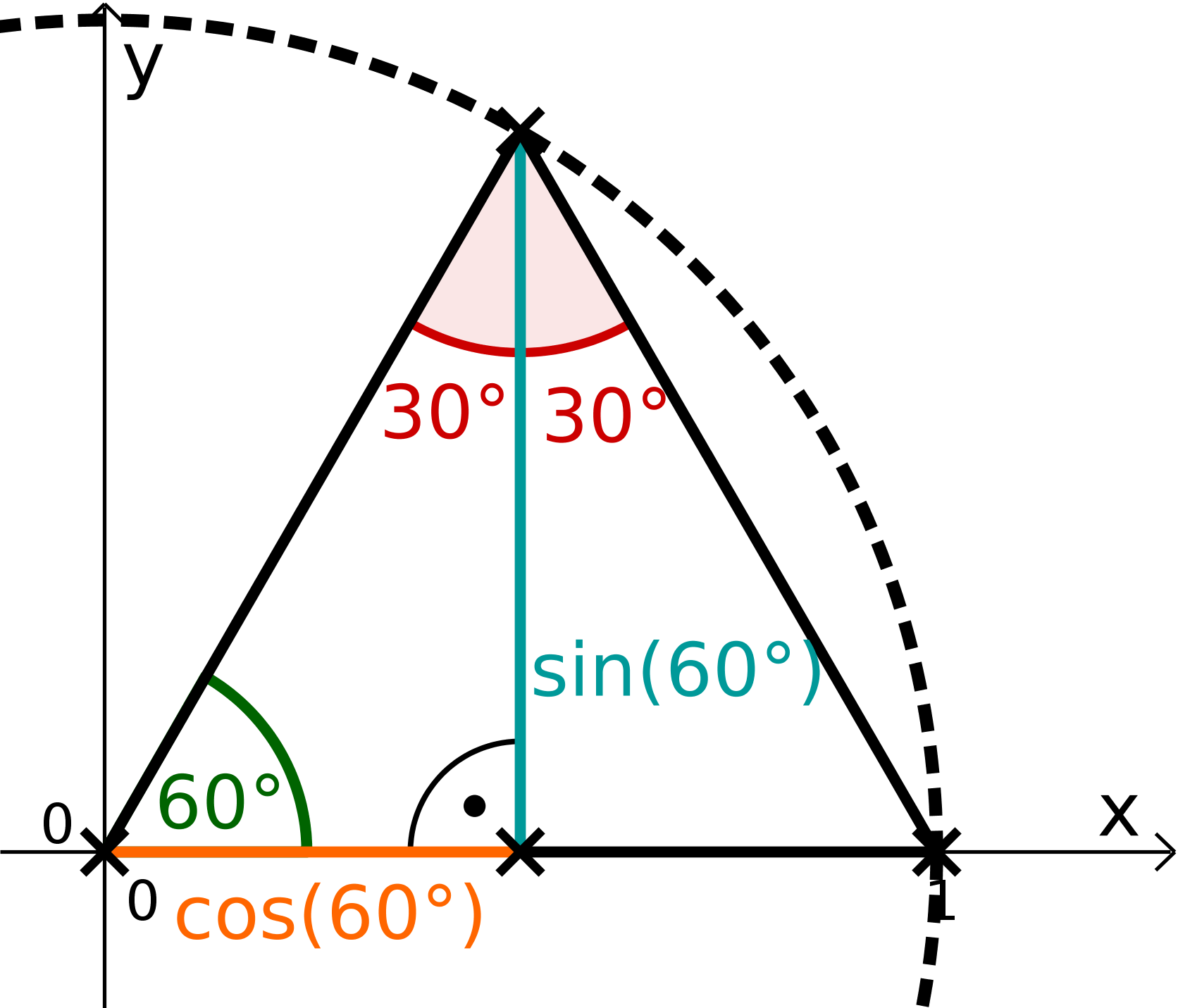
Zeichne ein großes Koordinatensystem. . Konstruiere mit dem Zirkel den Einheitskreis und trage mit dem Geodreieck einen -Winkel an die -Achse. Konstruiere die Länge und messe sie mit dem Lineal.
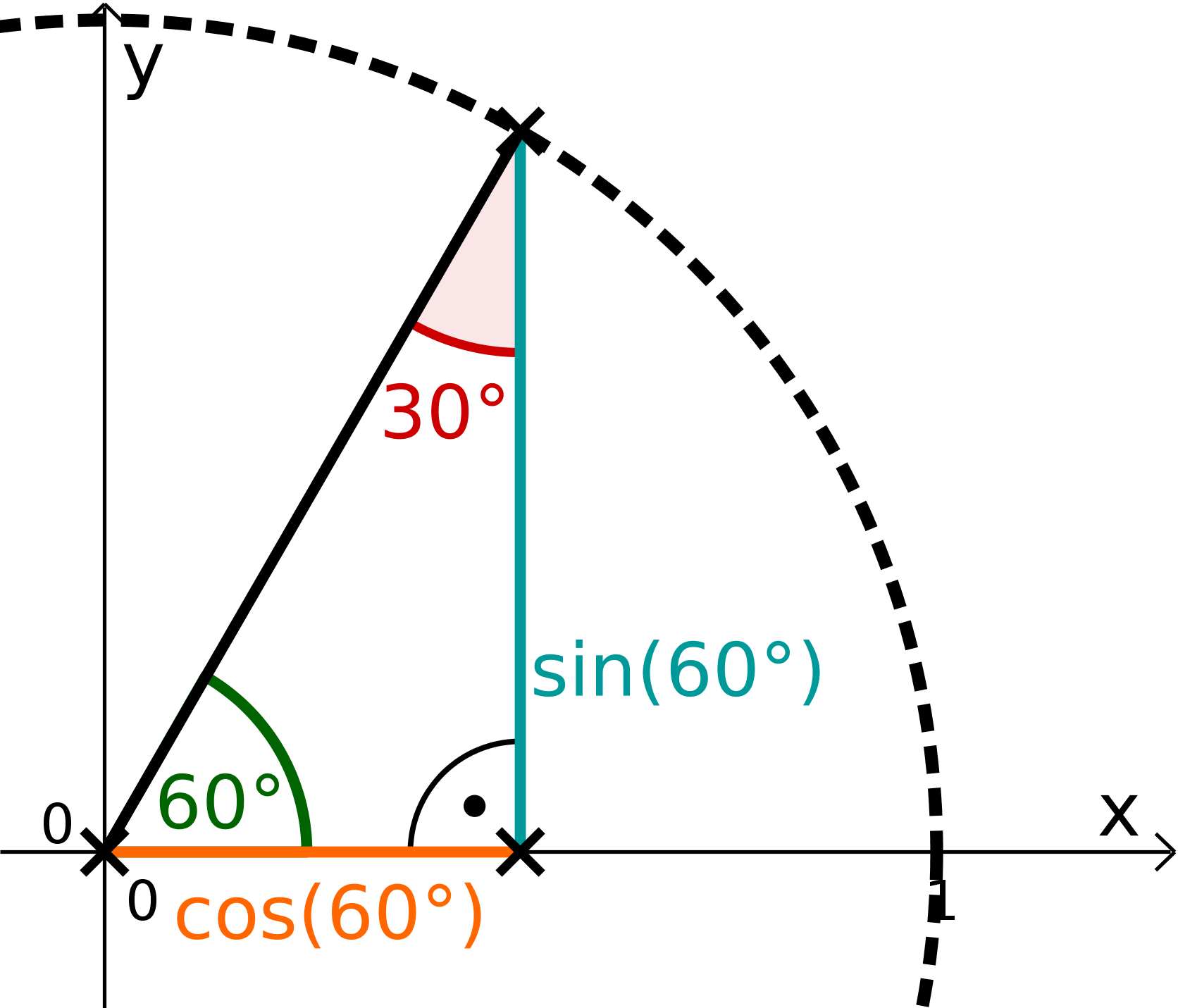
Berechne genau. Finde dafür zuerst den Wert für heraus. Konstruiere dafür ein gleichseitiges Dreieck.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?