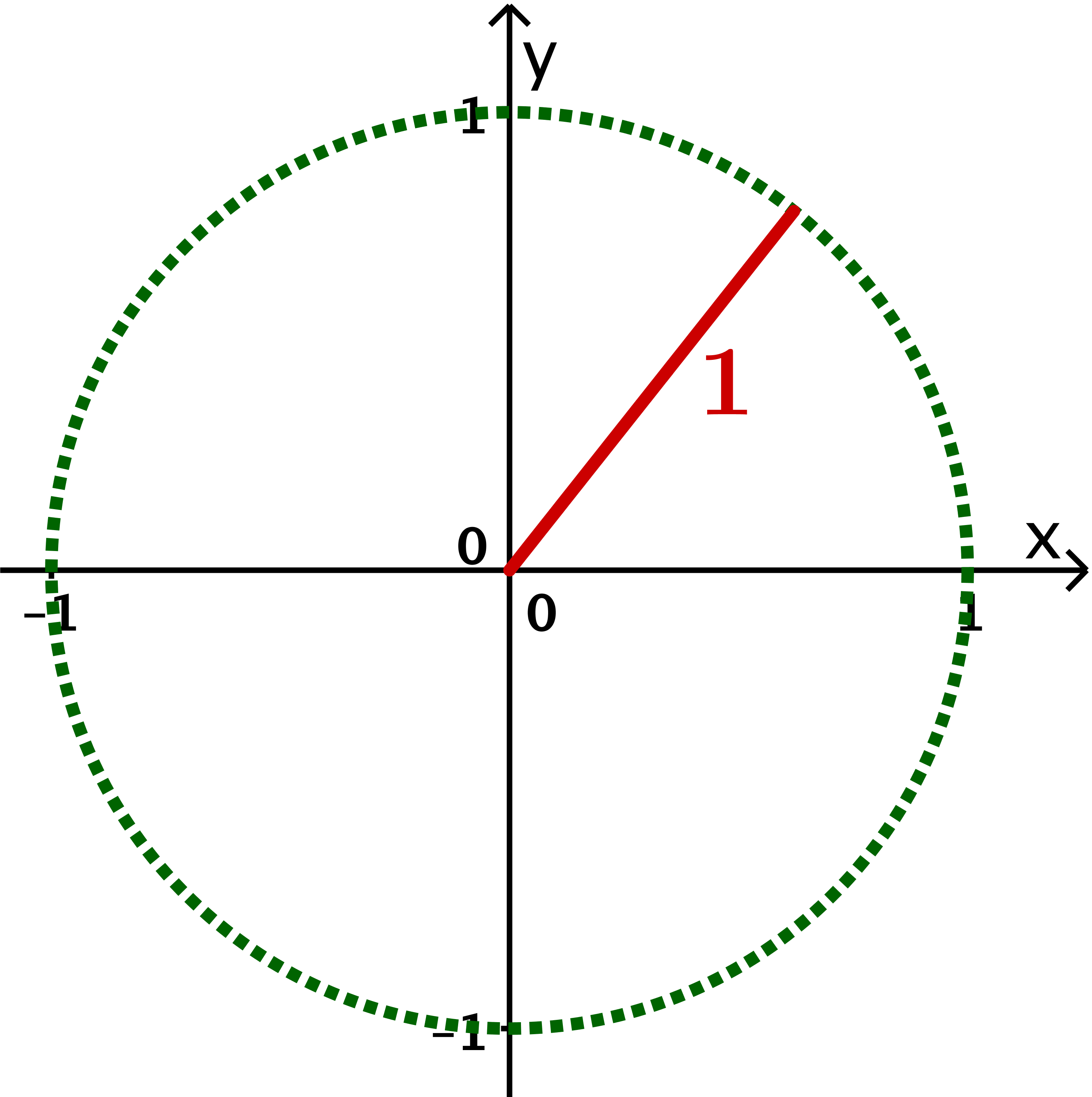
Der Einheitskreis ist der Kreis um den Ursprung eines Koordinatensystems mit Radius . Das bedeutet, er stellt die Menge aller Punkte dar, die vom Nullpunkt den Abstand haben.
So liegen beispielsweise die Punkte
auf dem Einheitskreis.
Anwendung
Am Einheitskreis lassen sich die trigonometrischen Funktion Sinus, Kosinus und Tangens veranschaulichen. Siehe hierzu den zugehörigen Artikel: Trigonometrie am Einheitskreis
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
