Gibt es einen Punkt und eine Spiegelachse, kann der Spiegelpunkt des Punktes an der Spiegelachse über mehrere Methoden bestimmt werden:
mithilfe des Geodreiecks oder
mithilfe eines Zirkels.
Das Spiegeln mithilfe des Zirkels heißt auch Konstruktion und ist meist genauer als das Spiegeln mit dem Geodreieck.
Ausgangslage
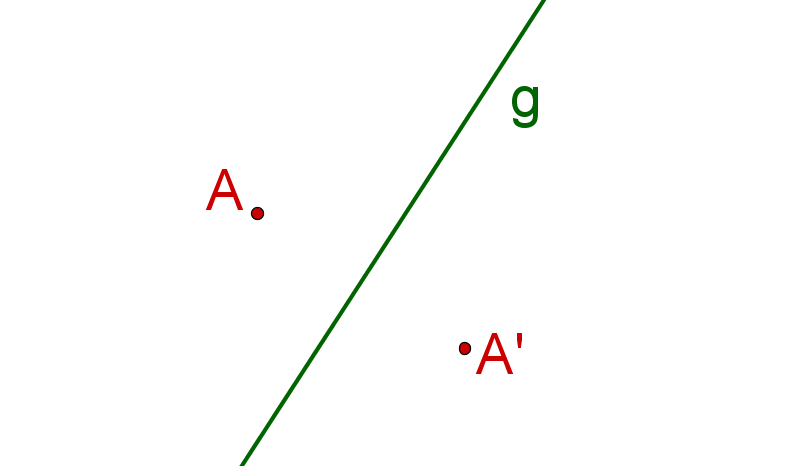
Gegeben sind ein Punkt und eine Spiegelachse . soll an gespiegelt werden.
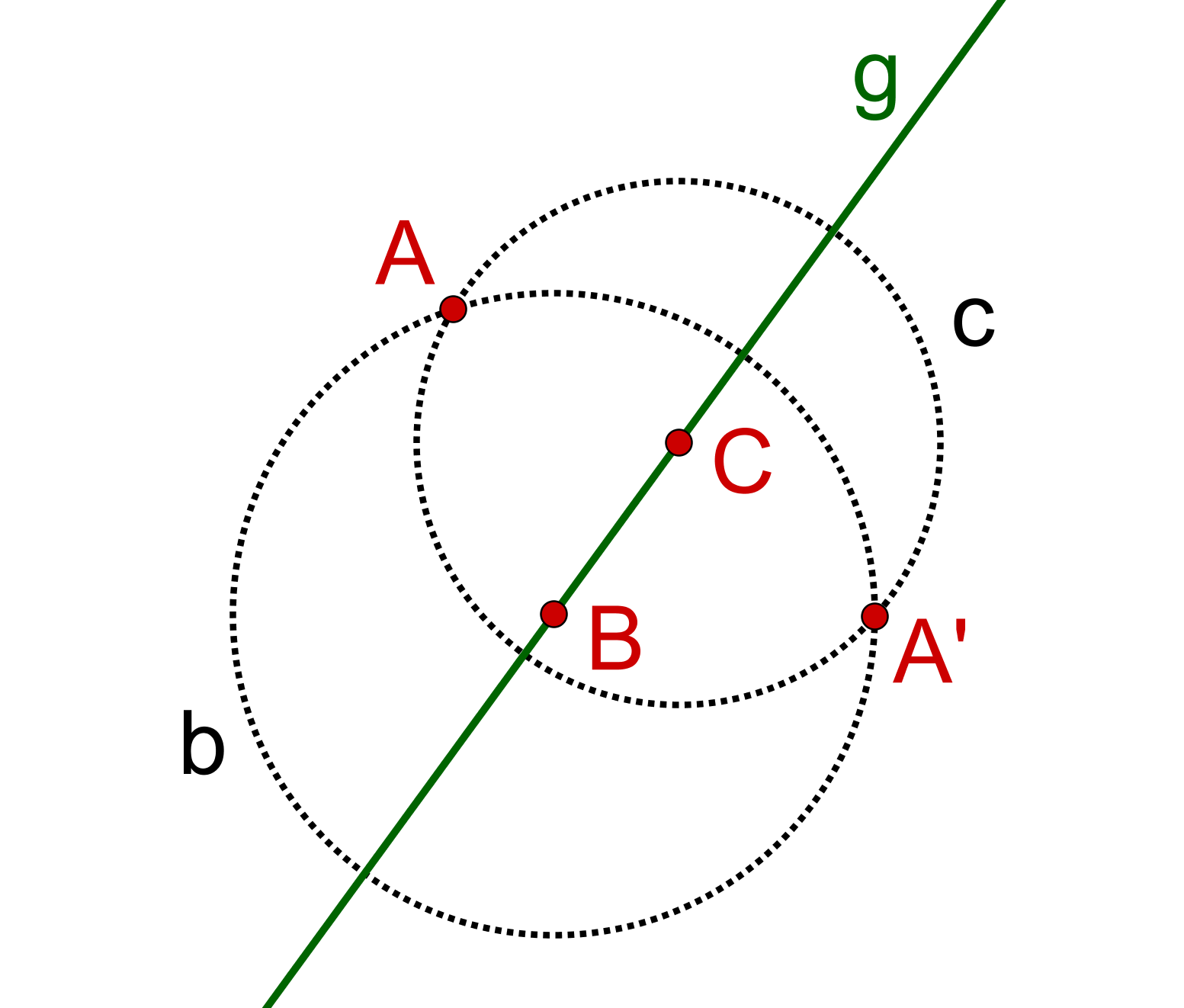
Konstruktion mit zwei Hilfskreisen
Allgemeines Vorgehen
Zeichne zwei verschiedene Punkte und auf ein.
Zeichne mit dem Zirkel einen Kreis () um den Mittelpunkt , der durch den Punkt geht.
Zeichne mit dem Zirkel einen weiteren Kreis (). Dieser soll den Mittelpunkt haben und durch gehen.
Die beiden Kreise und schneiden sich nun in zwei Punkten: und . Der Punkt ist der an der Geraden gespiegelte Punkt .
Animation zur Konstruktion
Ziehe am Schieberegler in der Animation, um die Schritte aus der Konstruktion nach und nach zu sehen.
Beispielaufgaben
Laden
Konstruktion mit Lot
Wie oben sind ein Punkt und eine Gerade gegeben. soll an gespiegelt werden.
Allgemeines Vorgehen
Konstruiere das Lot durch den Punkt an der Spiegelachse .
Ziehe mit dem Zirkel einen Kreis um den Schnittpunkt der Spiegelachse und des Lots .
Der Schnittpunkt des Kreises mit dem Lot ist der Spiegelpunkt .
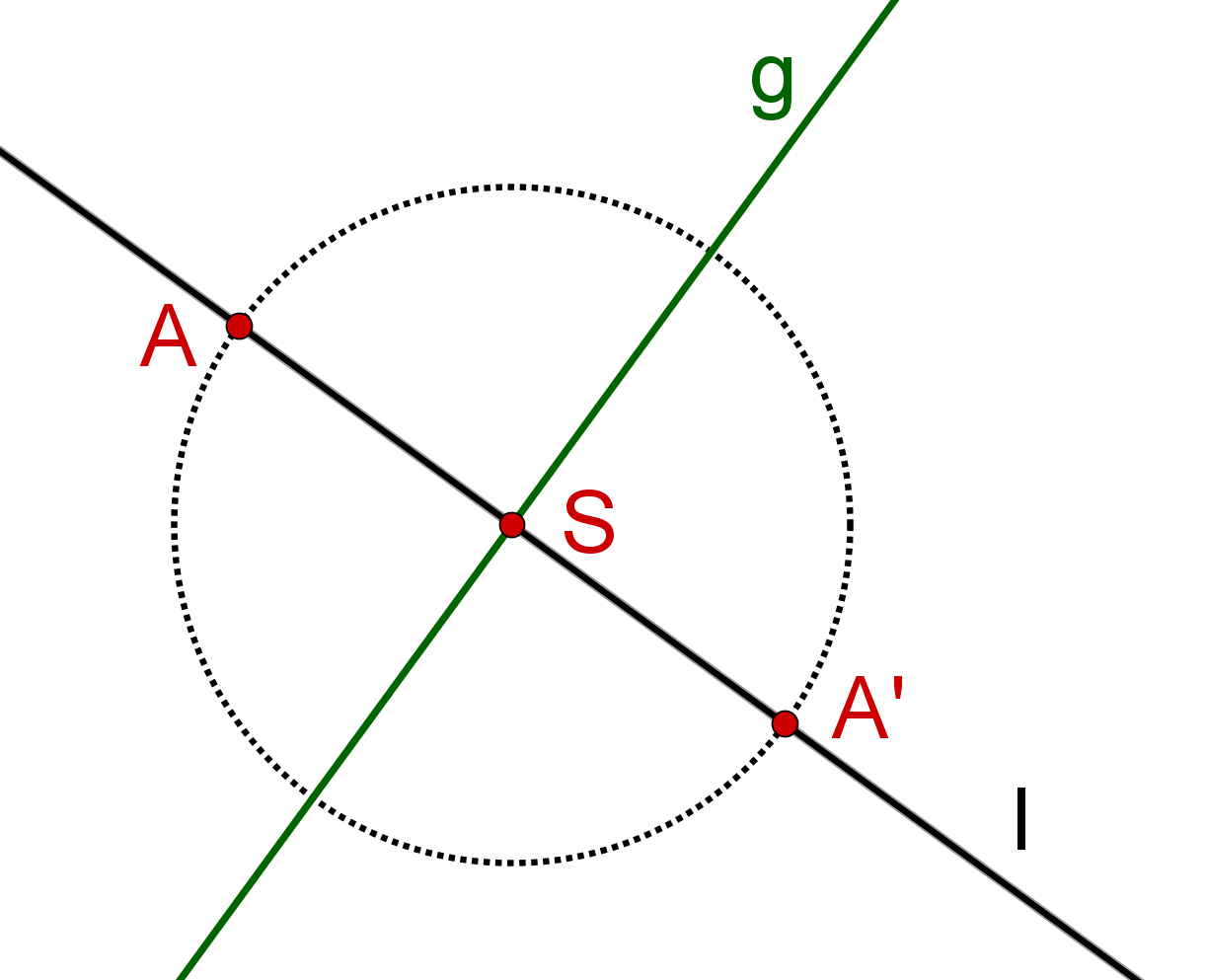
Animation zur Konstruktion
Ziehe am Schieberegler in der Animation, um die Schritte aus der Konstruktion nach und nach zu sehen.
Spiegeln mithilfe des Geodreiecks
In diesem Video wird erklärt, wie man mithilfe des Geodreiecks einen Punkt an einer Geraden spiegelt.
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
