Das Pascalsche Dreieck ist ein Schema von Zahlen, die in Dreiecksform angeordnet sind. Es kann beliebig weit nach unten erweitert werden.
Konstruktion
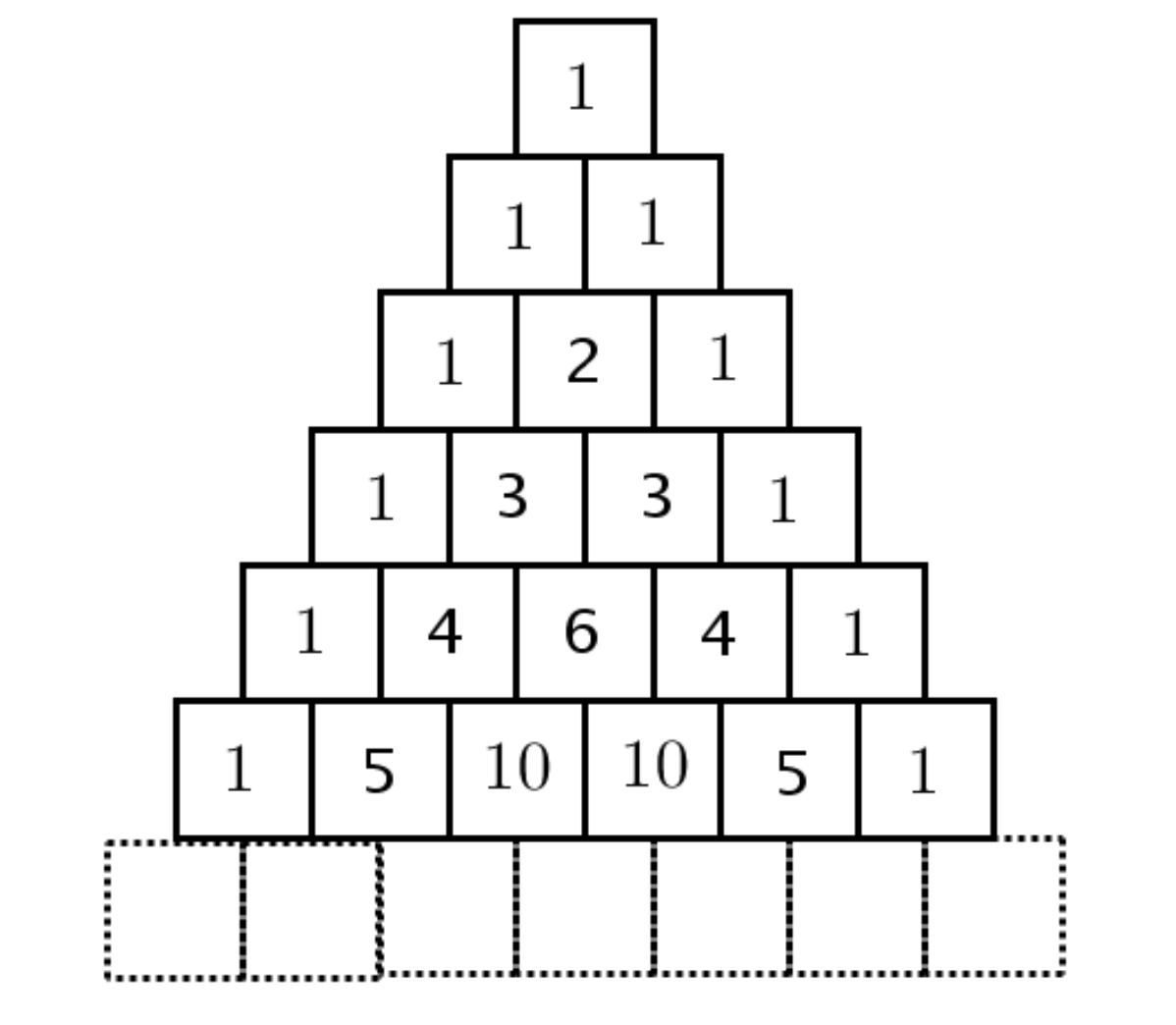
An der obersten Stelle steht eine eins. An allen anderen Stellen steht je die Summe der beiden Zahlen darüber.
Zusammenhang zu den Binomialkoeffizienten
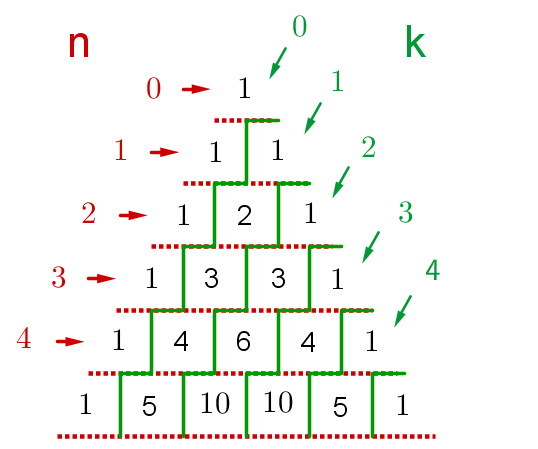
Am Pascalschen Dreieck kann man direkt die Binomialkoeffizienten ablesen.
Dazu nummeriert man die Kästchenzeilen (vertikal) und Kästchenspalten (horizontal) mit 0 beginnend. Der Wert von steht in der -ten Zeile im -ten Kästchen.
Warum?
Eine Möglichkeit, den Zusammenhang zu sehen, ist, sich vorzustellen, man stünde auf dem obersten Kästchen und wolle ein bestimmtes Kästchen erreichen, wobei man sich nur kästchenweise und immer nur abwärts bewegen darf. Dann entspricht in jedem Kästchen die Zahl darin genau der Anzahl der verschiedenen Wege dorthin.
Denn zu einem bestimmten Kästchen kann man nur über eines der beiden darüber gelangen, man darf sich ja nur abwärts bewegen. Die Gesamtanzahl der Wege zu diesem Kästchen ist also die Summe der Anzahl der Wege zu den beiden darüber. Das ist aber genau die Art und Weise, wie das Pascalsche Dreieck konstruiert ist!
Andererseits kann man die Anzahl der Wege auch über den Binomialkoeffizienten berechnen. Auf dem Weg nach unten in die -te Zeile (mit 0 angefangen zu zählen!)
trifft man nämlich mal die Entscheidung, nach links unten oder rechts unten zu gehen.

Will man in einer Zeile dann zum -ten Kästchen von links (wieder von 0 an) gelangen, muss man sich genau mal für "rechts" entschieden haben. Die Wege unterscheiden sich also nur darin, an welchen Stellen man sich für "rechts" entschieden hat. Zum Abzählen muss man also nur die Anzahl der Möglichkeiten berechnen, aus Stellen Stellen auszuwählen (die "rechts"-Schritte).
Das ist dann aber genau eine der wichtigsten Anwendungen des Binomialkoeffizienten
Die Zahlen im Pascalschen Dreieck lassen sich also einerseits rekursiv über die Summe der darüberliegenden Kästchen berechnen, oder direkt mithilfe des Binomialkoeffizienten.
Zusammenhang zu binomischen Formeln
Die Zeilen des Pascalschen Dreiecks sind hilfreich beim Ausmultiplizieren von Klammern der Form

Die (relativ komplizierte) allgemeine Formel lautet:
