Binomialkoeffizient

Der Binomialkoeffizient ist eine mathematische Funktion, mit der man Aufgaben aus der Kombinatorik lösen kann.

Ein bekanntes Beispiel ist das Lotto, das man auch "6 aus 49" nennt und das nicht ohne Grund. Man zieht nämlich 6 unterscheidbare Kugeln aus einer Urne mit 49 Kugeln, ohne auf die Reihenfolge zu achten. Die Anzahl der Kombinationen ergibt sich zu:

(\binom{49}{6}) = 13.983.816

Formel des Binomialkoeffizienten

$(\binom{n}{k}) = \frac{n!}{k! \cdot (n - k)!}$

In der Kombinatorik wird diese Formel sehr oft verwendet, weshalb man diese Kurzschreibweise eingeführt hat.

Sprechweisen für den Binomialkoeffizienten

Es gibt zwei Sprechweisen, die etwa gleich gebräuchlich sind, deshalb sollte man beide kennen. $(\binom{n}{k})$ nennt man:

„n über k“
„k aus n“ (intuitiver, da $(\binom{n}{k})$ berechnet, wie viele Möglichkeiten es gibt $k$ Kugeln aus einer Urne mit $n$ Kugeln zu ziehen)

Berechnung des Binomialkoeffizienten

Ein einfacher Weg, einen Binomialkoeffizienten zu berechnen, besteht in folgender Herangehensweise:

Notiere die Fakultät von k unter dem Bruchstrich.
Notiere das Produkt der gleichen Anzahl von absteigenden Zahlen im Zähler.

Beispiel: $(\binom{8}{3}) = \frac{8 \cdot 7 \cdot 6}{1 \cdot 2 \cdot 3} = 56$

Begründung an einem Beispiel:

$(\binom{n}{3}) = \frac{n!}{3! \cdot (n - 3)!} = \frac{n \cdot (n - 1) \cdot (n - 2) \cdot (n - 3) \cdot . . . \cdot 3 \cdot 2 \cdot 1}{1 \cdot 2 \cdot 3 \cdot (n - 3) \cdot . . . \cdot 3 \cdot 2 \cdot 1}$

Man erkennt ganz gut, dass sich die Faktoren $(n - 3) \cdot . . . \cdot 3 \cdot 2 \cdot 1$ sowohl im Zähler, als auch im Nenner finden und sie sich wegkürzen lassen.

Interaktive Visualisierung

Hier gibt es eine interaktive Visualisierung, die anschaulich zeigt, wie sich die Kombinationen "k aus n" ergeben.

Eigenschaften des Binomialkoeffizienten

Der Binomialkoeffizient ist immer eine ganze Zahl größer oder gleich null.
Falls $k > n$ folgt: $(\binom{n}{k}) = 0$ . (Man kann nicht aus 49 Kugeln 50 ziehen.)
Symmetrie: $(\binom{n}{k}) = (\binom{n}{n - k})$

Additionstheorem: $(\binom{n + 1}{k + 1}) = (\binom{n}{k}) + (\binom{n}{k + 1})$

Sonderfälle des Binomialkoeffizienten

Laden

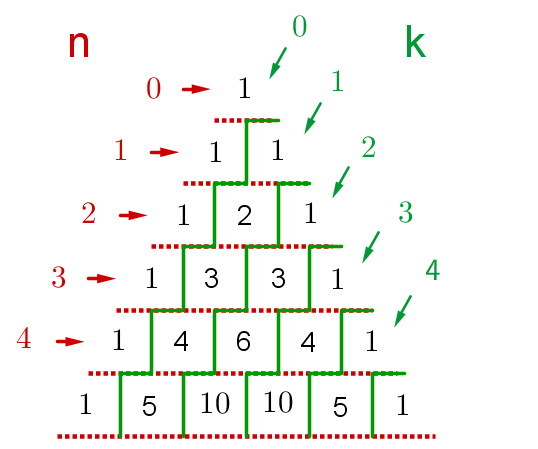
Pascalsches Dreieck

Die Werte der Binomialkoeffizienten kann man direkt am Pascalschen Dreieck ablesen.

Übungsaufgaben

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Binomialkoeffizienten

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?