Mithilfe eines Baumdiagramms kann man eine gesuchte Anzahl z. B. von Kombinationsmöglichkeiten bestimmen.
Wie das funktioniert, wird hier anhand von Beispielen erklärt.
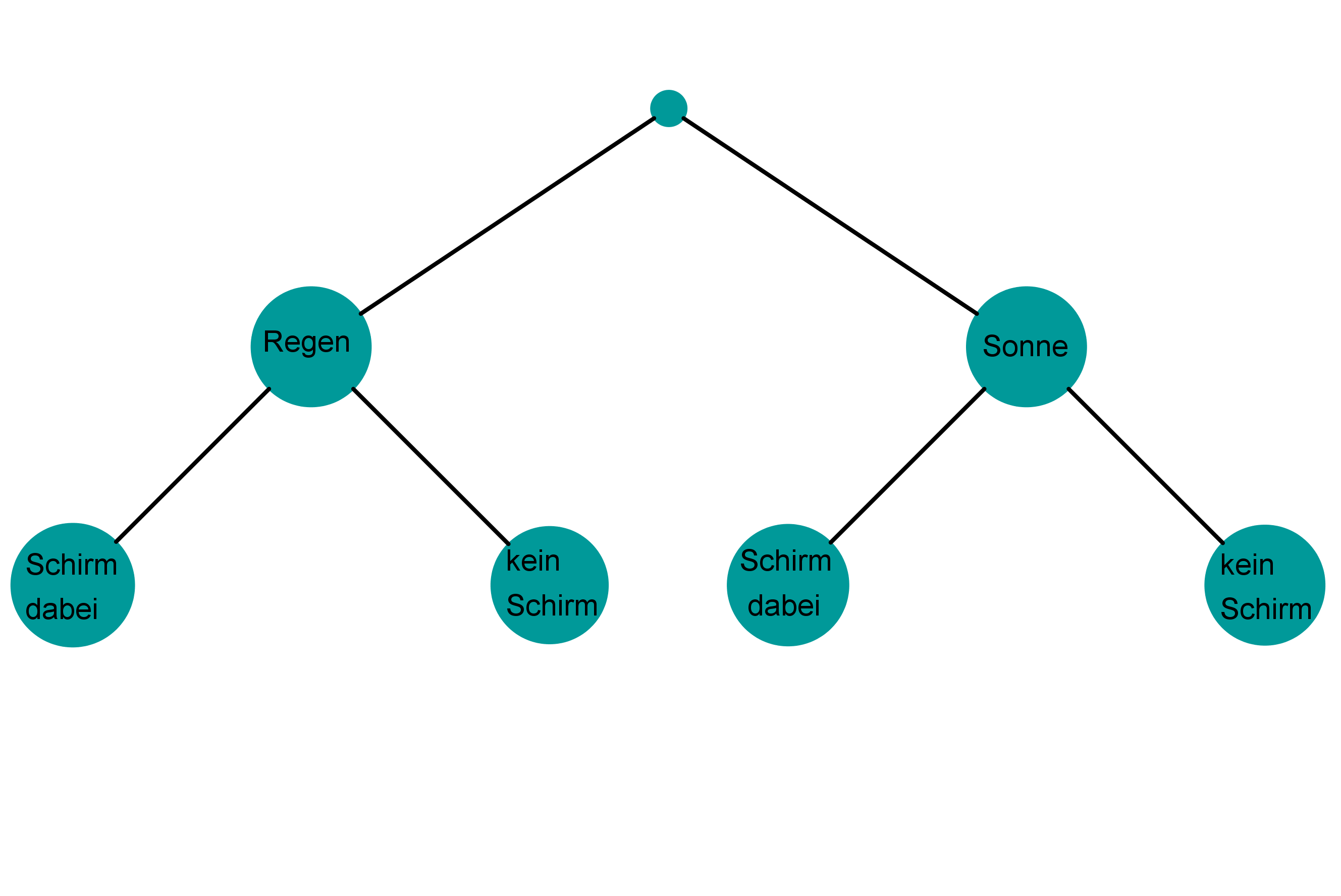
Beispiel 1
Laden
Schritt-für-Schritt-Lösung:
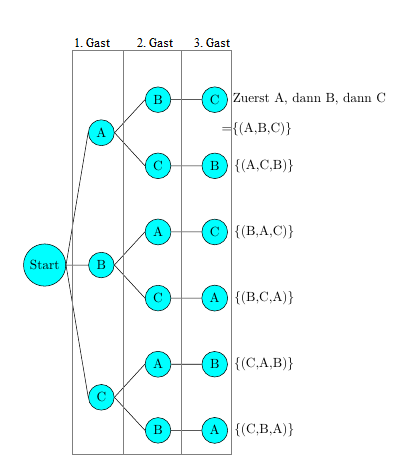
1. Man beginnt an einem Startpunkt. Das kann so aussehen wie rechts auf dem Bild oder auch einfach nur ein dicker Punkt sein. Jeder Ast, also jeder Weg, der von links nach rechts führt, beschreibt eine Möglichkeit, in welcher Reihenfolge die Gäste auf die Party kommen!

2. Welche Möglichkeiten gibt es für den ersten Gast? Es gibt drei: Angelika, Boris und Christoph. Hänge an den Startpunkt die Kürzel für ihre Namen.
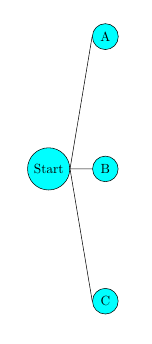
3. Der obere "Ast" bedeutet: "Angelika ist der erste Gast." Wie viele Möglichkeiten gibt es für den zweiten Gast? Es gibt zwei: Boris und Christoph. Hänge die Kürzel für ihre Namen an den "Angelika-Ast".
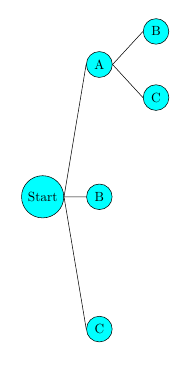
4. Der mittlere Ast bedeutet: "Boris ist der erste Gast", der untere Ast bedeutet: "Christoph ist der erste Gast." Aus dem gleichen Grund wie unter Punkt 3. folgt, dass man an B noch A und C, und an C noch A und B hängen muss.
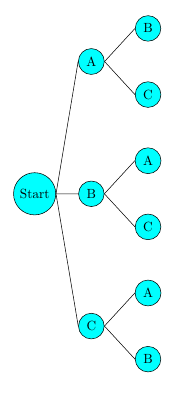
5. Als dritter Gast kommt jetzt jeweils nur derjenige in Frage, der nicht schon erster oder zweiter Gast war. Hänge also das Kürzel der Person als drittes an.
Hinter jedem Ende eines Astes wurde die Reihenfolge des Eintreffens notiert.
Beispiel 2
Laden
Schritt-für-Schritt-Lösung
1. Man beginnt an einem Startpunkt. Das kann so aussehen wie rechts auf dem Bild oder auch einfach nur ein dicker Punkt sein. Jeder Ast, also jeder Weg, der von links nach rechts führt, beschreibt eine Möglichkeit, einen Turm mit 3 Bauklötzen zu bauen!

2. Man unterscheidet die drei Farben rot, grün und blau. Stefans kleiner Bruder kann mit jeder der drei Farben beginnen. Hänge also die drei Möglichkeiten an den Startpunkt.
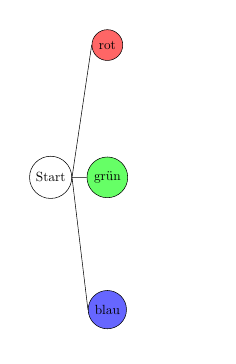
3. Im Folgenden werden die Farben durch R,G bzw. B abgekürzt. Wenn der kleine Bruder seinen blauen Bauklotz schon benutzt hat, bleiben ihm nur noch rot und grün:
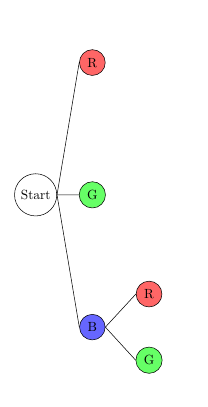
4. Wenn er blau und grün bereits benutzt hat, bleiben ihm nur noch rote Bauklötze; an den "B-G-Ast" wird also nur noch ein "R" angehängt.
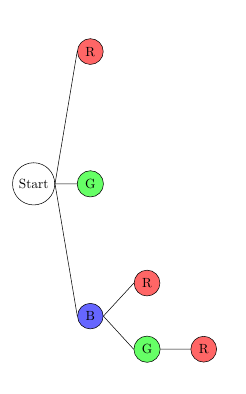
5. Nachdem er einen blauen und roten Stein benutzt hat, kann er noch zwischen rot und grün wählen, also werden an den "B-R-Ast" noch "R" und "G" gehängt.
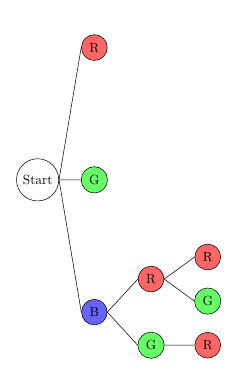
6. Beim Fall "zuerst grün" ist die Vorgehensweise die gleiche: Als zweiter Bauklotz kommen nur noch blau und rot in Frage, als dritter nur noch rot bzw. rot und blau.
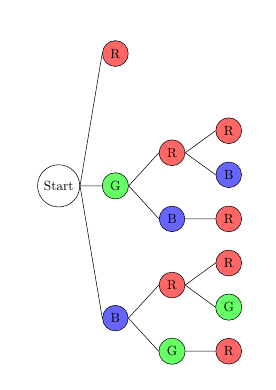
7. Wenn Stefans kleiner Bruder zuerst einen roten Bauklotz benutzt, hat er noch alle drei Farben zur Auswahl. Nachdem er den grünen Bauklotz benutzt hat, bleiben ihm noch der blaue und rote, nach dem blauen noch der grüne und rote. Wenn er als zweites auch einen roten Bauklotz nimmt, bleiben ihm für den dritten noch alle drei Farben zur Auswahl.
Bildausschnitt für den Fall "zuerst rot":
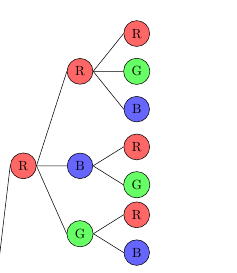
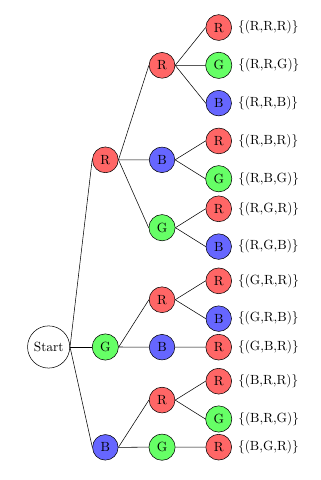
Der komplette Baum sieht so aus:
Man zählt die Möglichkeiten, also die Enden der Äste; es sind 13 Möglichkeiten.
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Baumdiagramm
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
