Als Hausaufgabe sollten die Schüler der Klasse 6 b mindestens 100-mal würfeln und die relativen Häufigkeiten, mit denen die einzelnen Augenzahlen aufgetreten sind, mithilfe einer Tabelle oder eines Diagramms darstellen.
Am nächsten Tag vergleichen Manfred, Peter, Klaus und Christian ihre Ergebnisse:
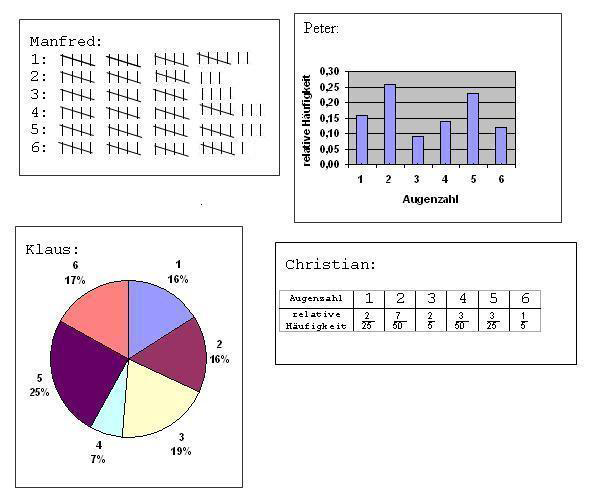
Nach einem kurzen Blick in Manfreds Heft sagt Christian: „Du hast wohl in der letzten Mathestunde nicht richtig aufgepasst!“ Wie kommt er dazu?
Klaus hat genau 200-mal gewürfelt. Wie oft hat er eine „6“ geworfen?
MalPeter betrachtet kurz die Diagramme und verkündet dann laut: „Christian hat von uns vier den besten Würfel. Bei ihm fällt am häufigsten die Sechs.“ Wie kommt Peter zu dieser Aussage? Glaubst auch du, dass Christian den besten Würfel hat?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
