Diskriminante

An der Diskriminante kann man ablesen, wie viele Lösungen die quadratische Gleichung besitzt: Für $D>0$ gibt es zwei, für $D=0$ eine und für $D<0$ keine Lösung.

Die Diskriminante D einer quadratischen Gleichung $ax^2+bx+c=0$ ist definiert durch:

\displaystyle {D=b^2-4ac}

Die Diskriminante stellt den in der Mitternachtsformel unter der Wurzel stehenden Term dar:

\displaystyle {D=b^2-4ac}

Zusammenhang zwischen Diskriminante und Nullstellen

Vorzeichen der Diskriminante	$D\ <\ 0$	$D\ =\ 0$	$D\ >\ 0$
Anzahl der Lösungen der Mitternachtsformel	keine Lösung, da keine negative Zahl unter der Wurzel sein darf	eine Lösung, da die Wurzel in der Mitternachtsformel 0 wird	zwei Lösungen wegen Plus und Minus in der Mitternachtsformel
Anzahl der Nullstellen	keine Nullstelle	eine doppelte Nullstelle	zwei einfache Nullstelle
Beispiel	$f(x)=x^2+2 \\ \Rightarrow a=1, b=0, c=2\\ \Rightarrow D=0^2-4 \cdot 1 \cdot 2=-8<0$	$f(x)=x^2-4x+4 \\ \Rightarrow a=1,b=-4,c=4 \\ \Rightarrow D=\left(-4\right)^2-4\cdot1\cdot4=0$	$f(x)=-x^2+1 \\ \Rightarrow a=-1,b=0,c=1 \\ \Rightarrow D=0^2-4\cdot\left(-1\right)\cdot1=4>0$
Graph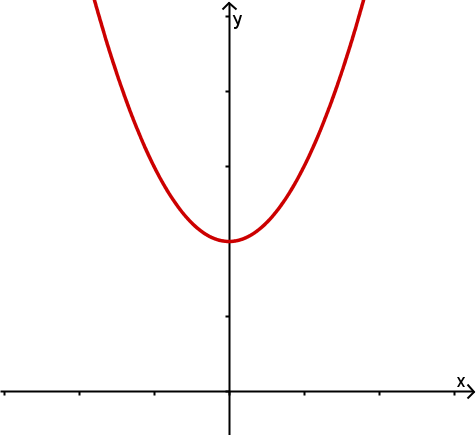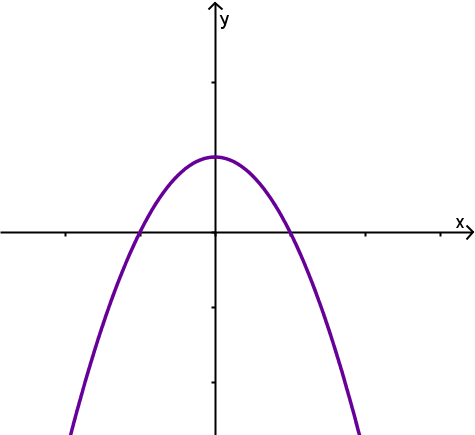

Zusammenhang von Diskriminante und Schnittstellen zweier Funktionen

Das Wissen über den Zusammenhang von Diskriminante und Nullstellen kann man nun benutzen, um Aussagen über die Existenz von Schnittpunkten von Funktionen zu machen:

Zur Berechnung der Schnittpunkte setzt man die zwei betreffenden Funktionen $f$ und $g$ gleich: $f(x)=g(x)$

Dies ist gleichbedeutend mit der Aussage $f-g=0$ . Daraus folgt nun, dass, falls der Ausdruck $f-g$ eine quadratische Funktion ist, die Diskriminante von $f-g$ die Aussage liefert, ob und wie viele Schnittpunkte existieren.

Vorzeichen der Diskriminante von $f-g$	$-$	$0$	$+$
Beispiel	$g(x)=-x^2-1 \\ f(x)-g(x)=x^2+1 - \left(-x^2-1 \right)=2x^2+2 \\ 2x^2+2=0 \\ D=0^2-4 \cdot 2 \cdot 2=-8$	$f(x)=x^2+1 \\ g(x)=-x^2+1 \\ f(x)-g(x)=x^2+1 - \left(-x^2+1 \right)=2x^2 \\ 2x^2=0 \\ D=0^2-4 \cdot 2 \cdot 0=0$	$f(x)=x^2 \\ g(x)=-x^2+2 \\ f(x)-g(x)=x^2 - \left(-x^2+2 \right)=2x^2-2 \\ 2x^2-2=0 \\ D=0^2-4 \cdot 2 \cdot (-2)=16$
Schnittpunkte	Kein Schnittpunkt	Ein Schnittpunkt bei $(0{,}1)$	zwei Schnittpunkte: nach Rechnung erhält man $(-1{,}1)$ und $(1{,}1)$
Graph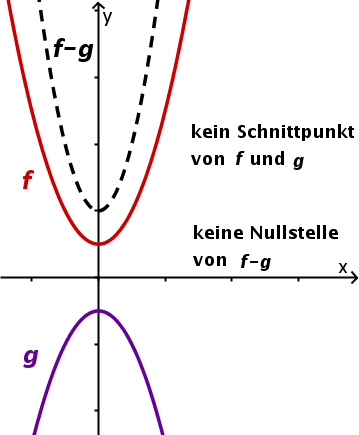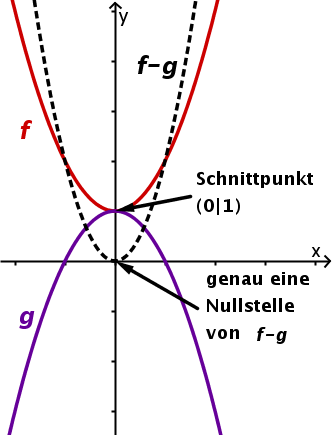

Video zum Thema Diskriminante

Laden

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?