Aufgaben zum Thema Maßstab
Du möchtest üben, mit Maßstäben zu rechnen? Hier findest du verschiedene Sachaufgaben dazu.
- 1
Ein Architekt möchte einen Plan von seinem Haus zeichnen. Er weiß, dass das Wohnzimmer 8 m lang ist und der Plan einen Maßstab von 1:100 haben soll. Wie lang muss das Wohnzimmer in seinem Plan sein?
cm - 2
Auf einer Karte beträgt die Entfernung von zwei Städten 5 cm. Der Maßstab ist mit
1 : 1 000 000 angegeben.
Berechne, wie weit die beiden Städte in Wirklichkeit voneinander entfernt sind.
km - 3
Das Rathaus einer Stadt ist vom Krankenhaus genau 400 m entfernt. Auf einer Stadtkarte sind es genau 8 cm. Welchen Maßstab hat diese Karte?
- 4
Ein Spielzeugmodell eines Flugzeugs ist 50 cm lang und der Maßstab ist als 1:100 angegeben. Es soll vom gleichen Flugzeug ein Ausstellungsmodell im Maßstab 1:25 gebaut werden. Wie lang wird das Ausstellungsmodell werden?
m - 5
Eine Mücke ist im Mikroskop 12 cm groß und der Maßstab des Mikroskops ist mit 24:1 angegeben.
Wie groß ist die Mücke wirklich?
- 6
Berechne den Maßstab einer Karte, bei der 2 cm auf der Karte in Wirklichkeit 5 km bedeuten.
- 7
Bei einer Modelleisenbahn ist ein 10 Meter langer Güterwagen nur 8 cm lang. Berechne den Maßstab für dieses Modell und berechne, wie groß ein Mensch in dieser Modelllandschaft ungefähr wäre.
- 8
Welche Höhe hat die Zugspitze () in einem Modell des Maßstabs ?
- 9
In einer Ausstellung wird ein Modell der Münchner Fußball-Arena im Maßstab 1:50 gezeigt. Das Modell ist lang, breit und hoch. Das Spielfeld hat im Modell einen Flächeninhalt von 4
Wie lang ist die Fußball-Arena in Wirklichkeit?
mEin Fußballfan möchte in seinem Garten ein Modell der Fußball-Arena im Maßstab aufbauen. Welche Höhe hat dieses Modell und wie groß ist der Flächeninhalt des Spielfelds in diesem Modell?
- 10
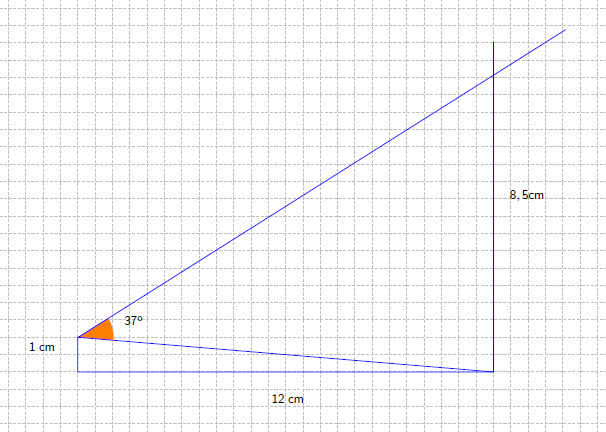
Im Urlaub fährt Sabine mit ihren Eltern nach Griechenland. Dort sieht sie eine Statue unter einem Winkel von 37° und ist 18m von ihr entfernt. Sabine ist 1, 50 m groß.
Fertige eine Skizze im Maßstab 1:150 an.
Wie groß ist die Statue in Wirklichkeit?
Gib die Lösung entweder in cm in der Form oder in m in der Form an.
- 11
Auf einer Wanderkarte ist der Maßstab vermerkt. Bei einer Wanderung legt man durchschnittlich in Minuten zurück.
Berechne, welche Strecke (in ) auf der Karte einer Wanderung von zweieinhalb Stunden entspricht.
cmDas nächste Rasthaus ist auf der Karte entfernt. Berechne, wie weit es entfernt ist und ob man es in einer Stunde Wanderzeit erreichen kann.
km
- 12
Die Planeten Merkur, Venus, Erde, Mars, Jupiter, Saturn, Uranus, Neptun und der Zwergplanet Pluto umkreisen unsere Sonne. In folgender Tabelle sind die Durchmesser der Sonne und der Planeten zusammengefasst:
Planeten (und ein Stern)
Durchmesser in km
Sonne
1.388.224
Merkur
4878
Venus
12099
Erde
12736
Mars
6763
Jupiter
142643
Saturn
119973
Uranus
51199
Neptun
49670
Pluto
2165
In einem Modell unseres Sonnensystems soll die Größe der Planeten maßstabsgetreu dargestellt werden. In diesem Modell soll der Durchmesser der Erde betragen.
Wie groß sind in diesem Modell die anderen Planeten?
Die Erde wird vom Mond umkreist. Der Durchmesser des Erdmondes beträgt . Wie groß ist dieser im Modell?
Gib das Ergebnis in an und runde auf zwei Stellen nach dem Komma.
mm
- 13
In einer Karte ist die Strecke von Bochum nach Essen, die in Wirklichkeit beträgt, lang. In welchem Maßstab ist die Karte dargestellt?
km - 14
Berechne, wie lang die angegebene Strecke auf der Karte angesichts des Maßstabs in Wirklichkeit ist.
17cm bei Maßstab 1:250.000
km
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?