Aufgaben zur Darstellung von Prozentangaben in Diagrammen
Wie gut kennst du dich mit Diagrammen aus? Lerne mit diesen Aufgaben Prozentangaben mithilfe von Diagrammen darzustellen!
- 1
Bei der Klassensprecherwahl der Klasse 7c werden 30 Stimmen abgegeben. Nach dem Auszählen ist klar, dass Anna mit 12 Stimmen Klassensprecherin geworden ist. Erich bekam 3, Tobias 6 und Moritz 9 Stimmen.
Stelle das Ergebnis der Wahl in einem Säulendiagramm dar. Auf der senkrechten Achse sollen die Prozentsätze abgetragen werden.
- 2
An einer Schule wurde eine Umfrage nach dem letzten Urlaubsziel gestartet. Die Schule besuchen insgesamt 1090 Schüler*innen.
Land
Anzahl
Land
Anzahl
Deutschland
234
Spanien
206
USA
41
Frankreich
34
Italien
198
Sonstige
205
Türkei
172
Stelle die Prozentsätze in einem Kreisdiagramm und einem Säulendiagramm dar.
- 3
In der Klasse 2a soll jedes Kind seine Lieblingssportart angeben. Das Ergebnis lautet:
Fußball: 12
Tischtennis: 8
Handball: 6
Schwimmen: 4
Die Klasse hat insgesamt 30 Kinder.
Berechne zuerst die Prozentsätze und nutze diese um die Verteilung der Lieblingssportarten in einem Kreisdiagramm darzustellen.
- 4
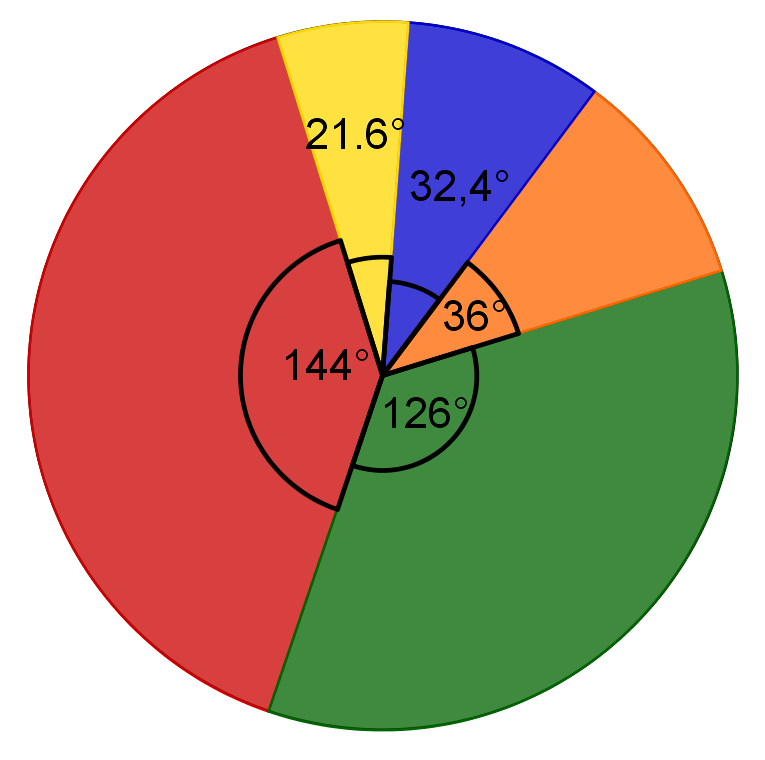
In dem nebenstehenden Diagramm siehst du die Verteilung einer Umfrage über Haustierbesitzer. Die Werte beziehen sich auf eine Grundmenge von 500 Personen.
Gib jeweils den prozentualen Anteil der jeweiligen Tierbesitzer an.
Legende: Hund - rot ; Katze - grün ; Nagetier - orange ; Vogel - blau ; Sonstige - gelb
- 5
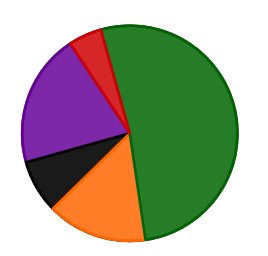
Ordne folgende Prozentzahlen den nebenstehenden zu:
15%
5%
20%
52%
8%
- 6
Im Jahr 2013 wurden über 500 Jungen im Alter von 5-9 Jahren zu ihrem Wunschberuf befragt. Stelle diese in einem Säulendiagramm dar.
Wunschberuf
In Prozent
Tierarzt
6,3%
Fußballspieler
5,7%
Polizist
5,7%
Pilot
4,6%
Arzt
3,6%
Rennfahrer
3,6%
- 7
An deiner Schule wurden Schüler befragt, wie sie zur Schule kommen. Dabei wurden folgende Angaben gemacht:
Verkehrsmittel
Anzahl der Schüler
zu Fuß
60
Roller
30
Fahrrad
70
Auto
40
Stelle das Ergebnis der Schülerbefragung in den verschiedenen Schaubildern mit den entsprechenden Prozentangaben dar:
Säulendiagramm
Balkendiagramm
Streifendiagramm
Kreisdiagramm
- 8
Herr Reiter hat am Anfang des Jahres ein Reitgeschäft eröffnet. Sein Startkapital betrug 200€. Nach 4 Monaten hält er in folgender Tabelle seine monatlichen Finanzzuwächse und -rückgänge fest:
Monat
Gewinn/Verlust in €
Januar
-100 €
Februar
20 €
März
60 €
April
-108 €
Stelle folgende Tabelle in einer Plus-Minus-Darstellung mit den entsprechenden Prozentsätzen dar.
- 9
In der Klasse 8c werden die Klassensprecher gewählt. Jedes Klassenmitglied hat eine Stimme. Es lassen sich Tim, Lisa, Max, Tobi und Tina zur Wahl aufstellen. Die Wahl ergab folgendes Ergebnis:
Kandidat
Anzahl der Stimmen
Tim
5
Lisa
4
Max
9
Tobi
4
Tina
3
Stelle das Wahlergebnis in einer Halbkreisdarstellung mit Prozentangaben dar.
- 10
In der Klasse 8b werden alle Schüler nach ihrer Lieblingssportart befragt. Jeder Schüler darf eine Sportart bei der Befragung angeben. Folgende Auswertung zeigt die Lieblingssportarten:
Lieblingssportart
Anzahl der Schüler
Fußball
9
Tanzen
3
Handball
4
Turnen
6
Sonstiges
3
Stelle die Tabelle in einem Streifendiagramm mit Prozentangaben dar.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
