Aufgaben zu Primzahlen
In den folgenden Aufgaben kannst du dein Wissen zu Primzahlen festigen und erweitern.
- 1
Primzahlzwillinge und Primzahldrilling
Ein Primzahlzwilling besteht aus zwei Primzahlen, deren Differenz zwei ist z.B. (5,7). Gib alle Primzahlzwillinge zwischen 1 und 100 an.
Primzahldrillinge werden entsprechend den Primzahlzwillingen festgelegt, z. B. (3,5,7). Gib alle Primzahldrillinge zwischen 0 und 100 an.
- 2
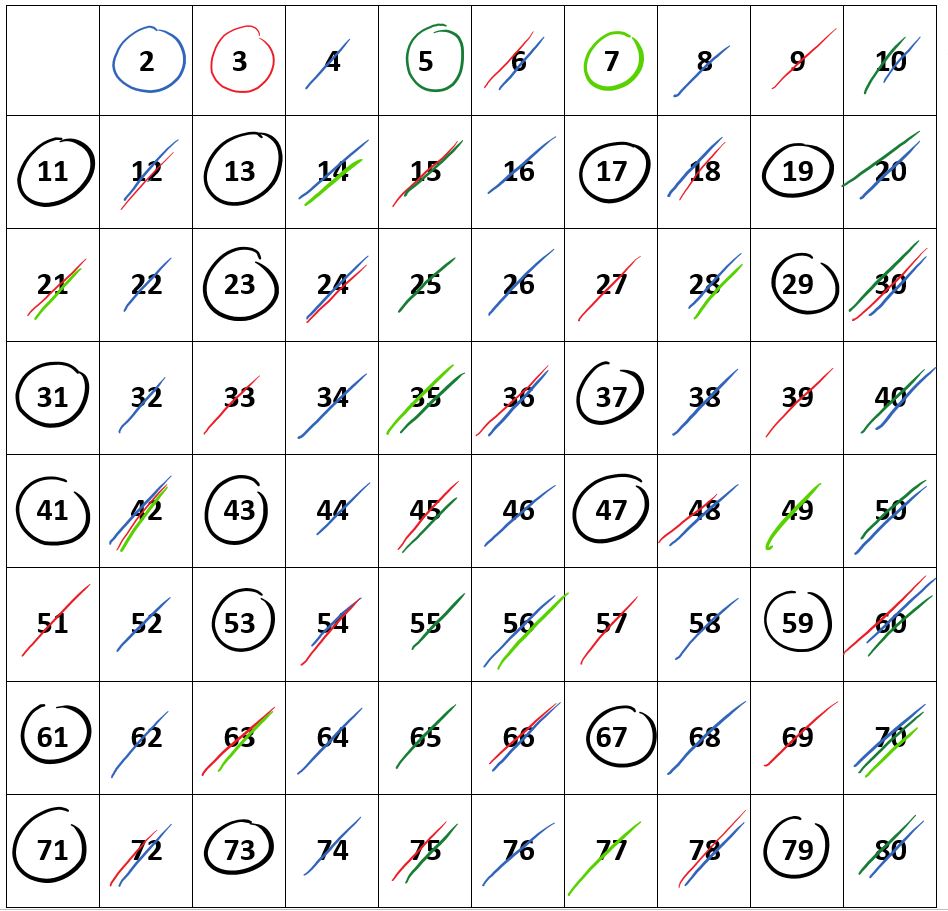
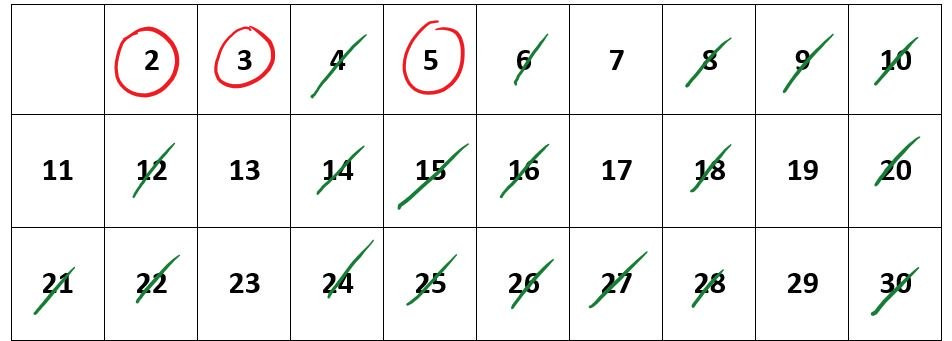
Ermittle nach dem Sieb des Eratosthenes alle Primzahlen der Liste von bis . Im folgenden Video werden beispielhaft die ersten Schritte des Verfahrens dafür gezeigt. Ergänze die weiteren Verfahrensschritte, die nicht im Video gezeigt werden, bis du alle Primzahlen der Liste bestimmt hast. Andernfalls kannst du sofort damit beginnen, die vollständige Liste nach dem Verfahren zu bearbeiten.
Laden
- 3
Wieso ist 1 keine Primzahl?
- 4
Beim Ermitteln der Primzahlen nach dem Sieb des Eratosthenes lässt sich folgendes feststellen: Die Verfahrensschritte müssen in einer Liste nur für alle Primzahlen mit angewendet werden. Denn die Vielfachen von Primzahlen mit sind bereits durchgestrichen.
Erkläre diesen Zusammenhang!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?