Um Längeneinheiten ineinander umrechnen zu können, muss man zunächst wissen, wie sie sich zueinander verhalten. So entspricht zum Beispiel ein Meter 100 Zentimetern oder ein Kilometer 1000 Metern. Mit diesem Wissen kann man z. B. eine Einheitentabelle erstellen.

Umrechnen mittels Einheitentabelle
Hier sind zusätzlich zu Kilometern, Metern und Zentimetern noch Dezimeter und Millimeter eingetragen.
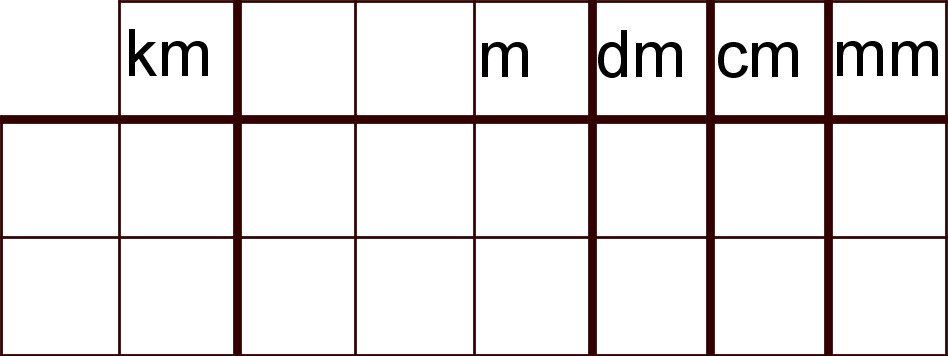
1000 Meter entsprechen einem Kilometer, also braucht man drei Stellen, an denen man Meter eintragen kann. Zehn Dezimeter entsprechen einem Meter, also braucht man eine Stelle für sie. Ebenso braucht man nur eine Stelle für Zentimeter und Millimeter, da zehn Zentimeter einem Dezimeter und zehn Millimeter einem Zentimeter entsprechen.
Wie kann man jetzt mit so einer Tabelle rechnen?
Ein paar Beispiele:
Wie viele Meter sind 1,234 Kilometer? Wie sieht eine gemischte Schreibweise aus?
Das Komma entspricht in der Tabelle dem Trennstrich rechts der Kilometerstelle. 1,234 Kilometer entsprechen also 1234 Metern, oder auch 1 Kilometer und 234 Metern.
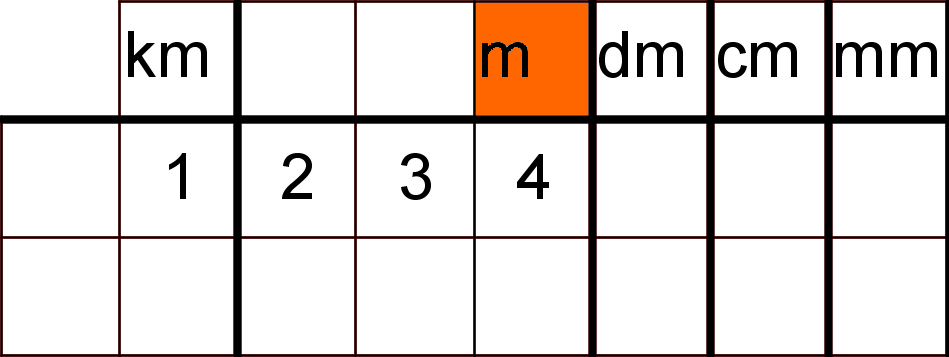
Also:
Wie viele Meter sind 42 Zentimeter?
Man möchte also Meter ablesen, in der Spalte steht aber zunächst nichts. Also muss man dort noch eine Null hinzufügen, nachdem man die 42 Zentimeter eingetragen hat. Diesmal entspricht der Trennstrich nach den Metern dem Komma. 42 Zentimeter entsprechen also 0,42 Metern.
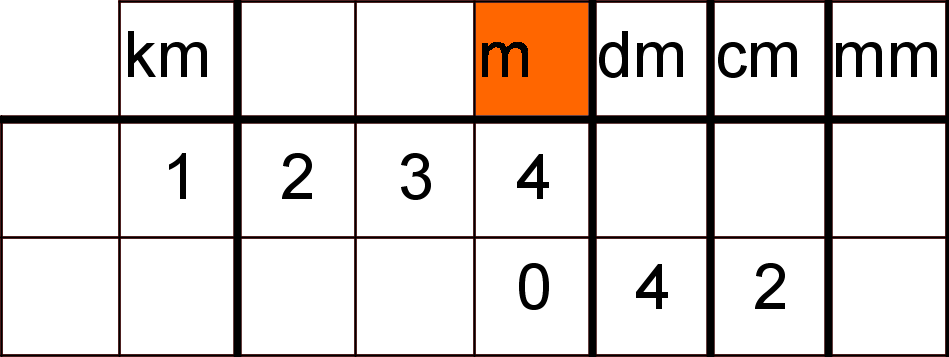
Also: Für eine gemischte Schreibweise gibt es hier zwei sinnvolle Möglichkeiten: oder
Wie viele Zentimeter sind 88 Meter?
Hier möchte man die Zentimeter ablesen. Dafür muss man zunächst Nullen an der Zentimeter- und Dezimeterstelle eintragen. Nun kann man erkennen, dass 88 Meter 8800 Zentimetern entsprechen.
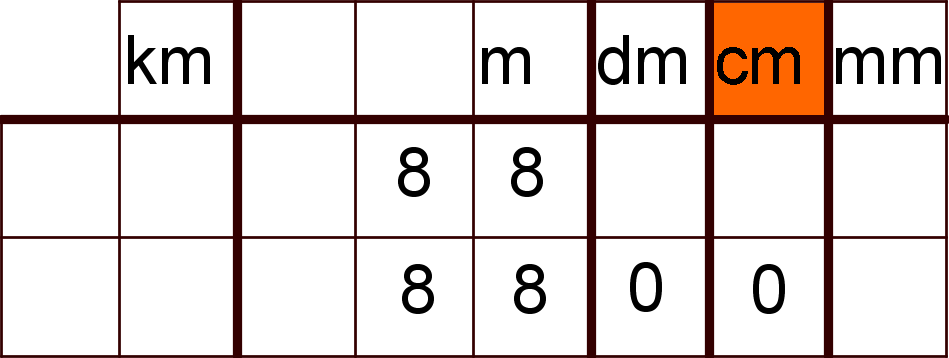
Also:
Typische Fehler:
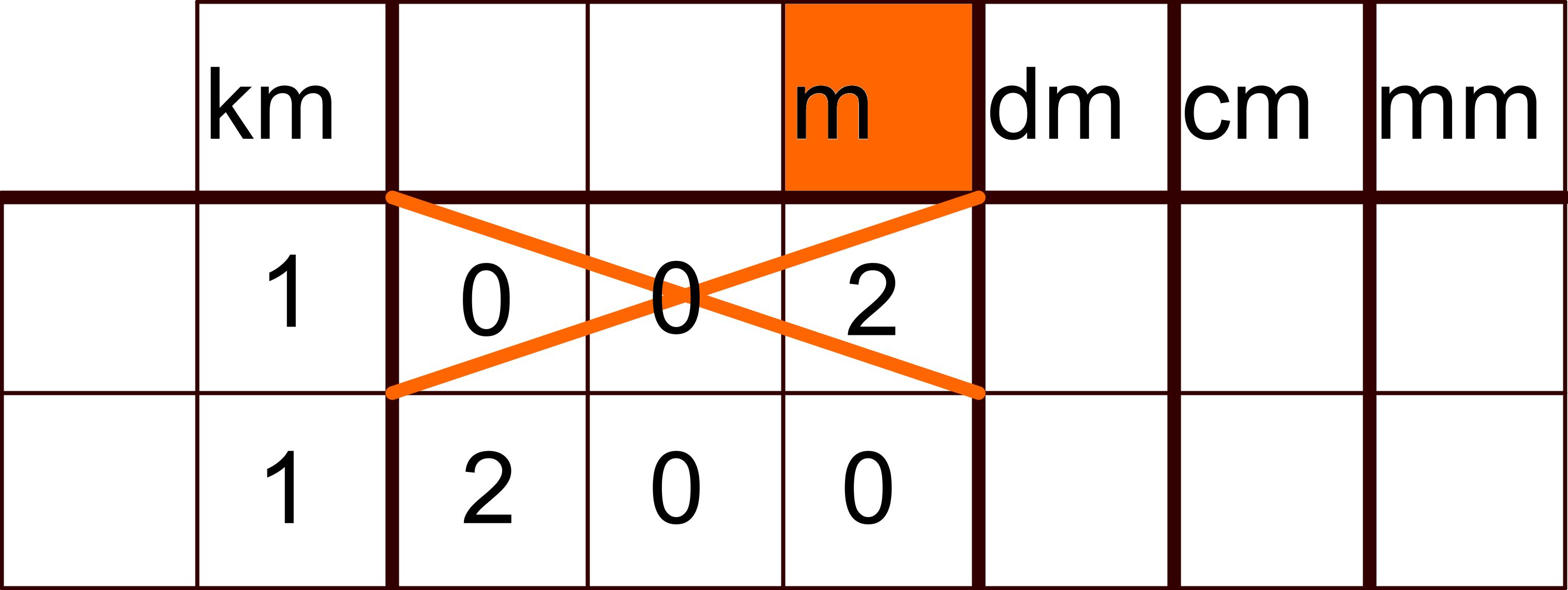
"Rechne 1,2 km in m um."
Antwort: ~~1002 m~~ 1200 m Die Nachkommastellen werden direkt am Kilometer-Trennstrich geschrieben und nicht am rechten Rand des Meterbereichs. Dann werden Nullen ergänzt!
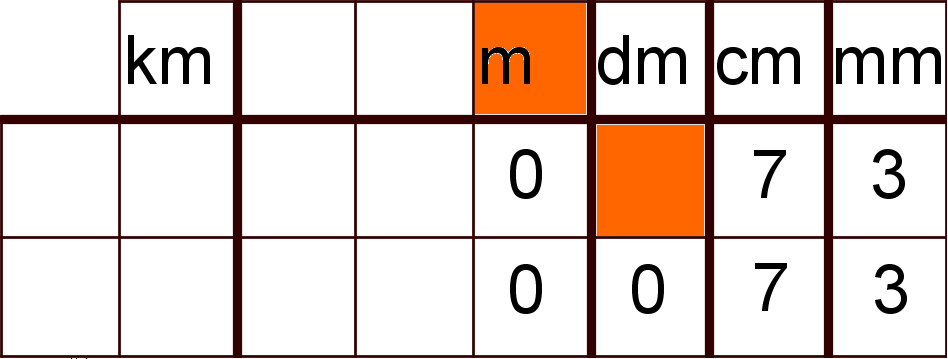
"Rechne 73 mm in m um."
Antwort: ~~0,73 m~~ 0,073 m Auch die leere Dezimeterstelle muss hier mit einer Null aufgefüllt werden.
Umrechnen mittels Umrechnungsfaktor
Alternativ zur Einheitentabelle kann man Umrechnungsfaktoren verwenden. Dazu multipliziert man den ursprünglichen Wert mit dem Verhältnis von seiner Einheit und der Zieleinheit. Oft braucht man dabei Wissen über Dezimalbrüche bzw. Dezimalzahlen.
Ein paar Beispiele:
Wie viele Meter sind 1,234 Kilometer?
Trenne die Einheit vom Wert. | |||
| ↓ | |||
| ↓ | Ersetze die alte Einheit durch die neue mit einem passenden Umrechnungsfaktor (hier 1000 ). | ||
| ↓ | Ziehe Einheit und Wert wieder zusammen. | ||
Wie viele Meter sind 42 Zentimeter?
Trenne die Einheit vom Wert. | |||
| ↓ | |||
| ↓ | Ersetze die alte Einheit durch die neue mit einem passenden Umrechnungsfaktor (hier 0,01). | ||
| ↓ | Ziehe Einheit und Wert wieder zusammen. | ||
Vergleich zu Flächen- und Volumeneinheiten
Längeneinheiten | zum Vergleich: Flächeneinheiten | zum Vergleich: Volumeneinheiten |
|---|---|---|
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
