Volumeneinheiten dienen dazu, die Größe eines dreidimensionalen Rauminhalts oder Volumens angeben zu können.
Gebräuchliche Volumeneinheiten sind
der Kubikmeter (),
der Kubikdezimeter (),
der Kubikzentimeter () und
der Kubikmillimeter ().
Einen Kubikdezimeter nennt man auch einen Liter. Dieser wird mit dem Einheitenzeichen (zur besseren Unterscheidbarkeit auch oder im Alltagsgebrauch ) notiert. Davon abgeleitet stehen
für einen Hektoliter () und
für einen Milliliter, wobei ist.
Übersicht Volumeneinheiten
Bezeichnung | Einheitszeichen | |
|---|---|---|
Kubikmillimeter | ist das Volumen eines Würfels mit Kantenlänge . | |
Kubikzentimeter | ||
Milliliter | ||
Kubikdezimeter | ||
Liter | ||
Hektoliter | ||
Kubikmeter |
Gelegentlich findet man auch die Abkürzung statt für Kubikzentimeter. Diese ist jedoch veraltet und wird nur selten verwendet.
Umrechnungen
Volumeneinheiten muss man anders umrechnen als die entsprechenden Längeneinheiten oder Flächeneinheiten:
Immer wenn bei der Umrechnung der Längeneinheit der Faktor 10 verwendet wird, wird bei der Umrechnung der zugehörigen Flächeneinheit der Faktor 100 verwendet, und bei Umrechnung der zugehörigen Volumeneinheit der Faktor 1000.
Die folgende Tabelle gibt eine Übersicht:
Längeneinheiten | Flächeneinheiten | Volumeneinheiten |
|---|---|---|
Einheitentafel
Besonders leicht geht das Umrechnen mit der Einheitentafel:
Dazu legt man, von rechts beginnend, jeweils 3 Spalten für , , usw. an.
Wichtig ist also, dass man bei den Volumeneinheiten jeweils 3 Spalten reserviert, wo bei den Flächeneinheiten 2 Spalten stehen und bei den Längeneinheiten nur 1 Spalte ist.

Zum Umrechnen einer Volumenangabe trägt man die angegebene Größe bei der betreffenden Einheit ein, und zwar so, dass die Einerziffer bzw. das Komma der Zahl gerade dort steht, wo die angegebene Einheit beginnt / endet.
Freibleibende Plätze können mit Nullen aufgefüllt werden.
Beispiel
Eingetragen werden sollen
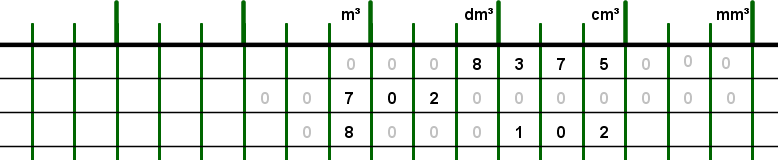
Aus der so ausgefüllten Einheitentafel kann man nun leicht die umgerechnete Volumenangabe ablesen.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Umrechnen von Volumeneinheiten
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
