imaginäre Einheit:
komplexe Zahl: mit
heißt Realteil und Imaginärteil von
Konjugiert Komplexe Zahl:
Betrag einer komplexen Zahl:
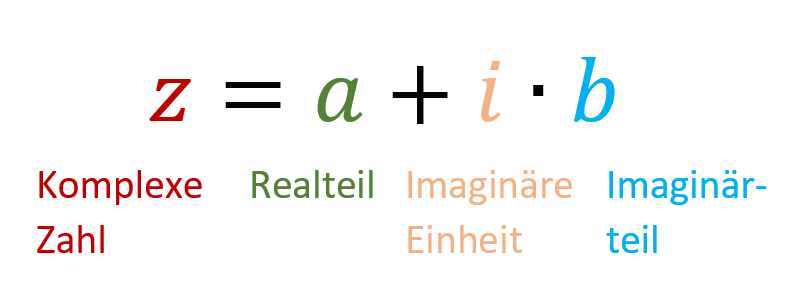
Was sind die komplexen Zahlen?
Die Gleichung hat in den dir bisher bekannten reellen Zahlen keine Lösung. Wenn es allerdings eine Zahl gäbe, die quadriert ergeben würde, wäre die Gleichung lösbar. In den reellen Zahlen gibt es eine solche Zahl nicht. Deswegen wird die Zahlenmenge der komplexen Zahlen eingeführt.
In den komplexen Zahlen gibt es die sogenannte imaginäre Einheit , also eine Zahl, die quadriert ergibt.
Damit kannst du die obige Gleichung lösen:
Eine komplexe Zahl lässt sich allgemein so schreiben:
wobei und reelle Zahlen sind. Diese Darstellung heißt kartesische Darstellung einer komplexen Zahl.
Man nennt den Realteil von . Man schreibt .
ist der Imaginärteil von . Man schreibt: .
Realteil und Imaginärteil sind also immer reelle Zahlen.
Beispiele
und sind komplexe Zahlen. Für und kannst du also beliebige reelle Zahlen einsetzen und du erhältst eine komplexe Zahl. Für ist der Realteil und der Imaginärteil . Für ist der Realteil und der Imaginärteil .
Auch ist eine komplexe Zahl. In diesem Fall ist und . Also ist und .
ist eine reelle Zahl, aber auch eine komplexe Zahl. In diesem Fall ist und . Also ist und .
Die reellen Zahlen sind eine Teilmenge der komplexen Zahlen
Die reellen Zahlen sind eine Teilmenge der komplexen Zahlen . Das bedeutet, dass jede reelle Zahl auch eine komplexe Zahl ist, aber nicht jede komplexe Zahl auch eine reelle Zahl ist.
Genauso sind zum Beispiel die natürlichen Zahlen eine Teilmenge der reellen Zahlen . Jede natürliche Zahl ist gleichzeitig auch eine reelle Zahl, aber nicht jede reelle Zahl ist auch eine natürliche. Zum Beispiel ist die natürliche Zahl auch eine reelle Zahl, aber die reelle Zahl ist keine natürliche Zahl.
Wichtige Begriffe
Das heißt, man ersetzt das Plus in der Mitte durch ein Minus.
Der Betrag wird auch oft mit dem Buchstaben bezeichnet.
Mit der konjugiert komplexen Zahl gilt außerdem:
Beispiele
Die konjugiert komplexe Zahl von erhältst du, indem du das Plus durch ein Minus ersetzt. Also ist die konjugiert komplexe Zahl .
Was ist die konjugiert komplexe Zahl von ? Hier steht kein Plus, sondern ein Minus in der Mitte. Allerdings kannst du umschreiben: . Nun kannst du das Plus durch ein Minus vertauschen, um die konjugiert Komplexe zu bilden:
Zusammenfassend kannst du dir also merken:
Um die konjugiert Komplexe zu bilden, machst du ein in der Mitte zu einem und ein in der Mitte zu einem .
Berechne außerdem die Beträge von und :
Bei ist und . Das setzt du in die Formel für den Betrag ein:
Bei ist und . Der Betrag ist damit:
Der Betrag der konjugiert komplexen Zahl ist genauso groß wie der Betrag der "ursprünglichen" komplexen Zahl .
Bei ist und . Der Betrag ist also:
Addition und Subtraktion zweier komplexer Zahlen
Du kannst zwei komplexe Zahlen addieren oder subtrahieren, indem du die Realteile addierst bzw. subtrahierst und anschließend die Imaginärteile addierst bzw. subtrahierst.
Allgemein:
Die Summe aus , , ergibt sich als
Beispiele
Addiere und . Das Ziel ist es, am Ende wieder eine komplexe Zahl der Form zu erhalten.
Schreibe die zwei komplexen Zahlen in Klammern und addiere sie. | |||
| ↓ | |||
| ↓ | Die Klammern kannst du weglassen, weil zwischen den Klammern nur ein + steht. | ||
| ↓ | Nun ordnest du: du bringst alle Zahlen ohne , also die Realteile nach vorne und alle Glieder mit nach hinten. Achte darauf, dass du die Vorzeichen mitnimmst. | ||
| ↓ | Jetzt kannst du die Zahlen vorne miteinander verrechnen und die Glieder mit verrechnen. | ||
Das bedeutet, die Summe von und ergibt wieder eine komplexe Zahl. Das ist das Endergebnis. Du kannst nicht weiter vereinfachen.
Subtrahiere von . Auch hier soll als Endergebnis wieder eine komplexe Zahl in ihrer "normalen", kartesischen Darstellung stehen.
Schreibe die komplexen Zahlen jeweils in Klammern und subtrahiere dann die Klammern. | |||
| ↓ | |||
| ↓ | Die vorderen Klammern kannst du weglassen, weil vor ihr quasi ein Plus steht. Die hintere Klammer ist eine Minusklammer, weil vor ihr ein Minus steht. Du kannst sie auflösen, indem du jedes Vorzeichen in der Klammer einmal umdrehst. | ||
| ↓ | Nun ordnest du: du bringst alle Zahlen ohne nach vorne und alle Zahlen mit nach hinten. Achte darauf, dass du die Vorzeichen mitnimmst. | ||
| ↓ | Nun kannst du die Zahlen vorne ohne miteinander verrechnen und sie Glieder mit . | ||
Wichtig bei der Subtraktion ist, dass du die komplexe Zahl, die du abziehst, in Klammern setzt. Dann erhältst du eine Minusklammer, die du durch Umdrehen aller Vorzeichen auflösen kannst.
Multiplikation zweier komplexer Zahlen
Du kannst zwei komplexe Zahlen miteinander multiplizieren, indem du die beiden komplexen Zahlen jeweils in Klammern setzt und anschließend wie gewohnt die Klammern ausmultiplizierst.
Allgemein:
Das Produkt aus , , ergibt sich als
Beispiele
Multipliziere und . Ziel ist es, am Ende wieder eine komplexe Zahl der Form zu erhalten.
Setze die beiden komplexen Zahlen jeweils in KIammern und verbinde die Klammern durch ein Malzeichen. | |||
| ↓ | |||
| ↓ | Jetzt kannst du die Klammern wie gewohnt ausmultiplizieren, also jedes Element der linken Klammer mit jedem Element der rechten Klammer multiplizieren. | ||
| ↓ | Das kannst du vereinfachen, um die Malzeichen wegzubekommen. | ||
| ↓ | Verwende, dass ist. | ||
| ↓ | Das letzte Glied kannst du nochmal vereinfachen, indem du ausrechnest. | ||
| ↓ | Jetzt ordnest du: Alle Zahlen ohne kommen nach vorne und alle Zahlen mit kommen nach hinten. Achte darauf, dass du die Vorzeichen der Zahlen immer mitnimmst. | ||
| ↓ | Nun kannst du die vorderen Zahlen ohne miteinander verrechnen und die Zahlen hinten mit . | ||
Das ist das Endergebnis. Du kannst nicht weiter vereinfachen.
Multipliziere und .
Setze die beiden komplexen Zahlen, die du miteinander multiplizieren willst jeweils in Klammern. Dann schreibst du ein Mal zwischen die Klammern. | |||
| ↓ | |||
| ↓ | Die Klammern kannst du wie gewohnt ausmultiplizieren - so als stünden ganz "normale" Zahlen darin. D.h. du multiplizierst jedes Element aus der linken Klammer mit jedem Element aus der rechten Klammer. | ||
| ↓ | Die einzelnen "kleinen" Produkte kannst du jetzt ausrechnen. z.B. ist , weil du die mit der multiplizieren kannst und anschließend das wieder dranhängst. Du kannst dir im Kopf vorstellen, dass wie eine Variable ist, also z.B. und dann wie gewohnt rechnen. | ||
| ↓ | Du weißt, dass , deswegen kannst du ausrechnen: | ||
| ↓ | Jetzt ordnen du: du bringst alle Glieder ohne nach vorne und alle Glieder mit nach hinten. Achte darauf, dass du die Vorzeichen der Zahlen immer mitnimmst. | ||
| ↓ | Jetzt verrechnest du alle Zahlen mit miteinander und alle Zahlen ohne . | ||
Teilen zweier komplexer Zahlen
Du kannst zwei komplexe Zahlen folgendermaßen durcheinander teilen:
Schreibe die Teilung als Bruch
Überlege dir die konjugiert komplexe Zahl des Nenners (also der Zahl unten im Bruch)
Erweitere den Bruch mit dieser konjugiert komplexen Zahl.
Multipliziere die nun entstandenen Klammern aus.
Du erhältst dann im Nenner eine reelle Zahl. Vereinfache den Zähler.
Teile jedes Glied des Zählers (also der Zahl oben im Bruch) durch die reelle Zahl im Nenner.
Beispiele
Teile durch .
Ziel ist es, am Ende wieder eine komplexe Zahl der Form zu erhalten. Dafür muss der Bruchstrich, der durch die Teilung entsteht, irgendwie wegkommen.
1) Schreibe die Teilung als Bruch | |||
| ↓ | |||
| ↓ | Setze für und die komplexen Zahlen aus der Angabe ein: | ||
| ↓ | 2) Überlege dir die konjugiert Komplexe Zahl vom Nenner, also von . Ersetze das durch ein , um die konjugiert komplexe Zahl zu erhalten. Die konjugiert Komplexe ist also: 3) Erweitere den Bruch mit dieser Zahl, d.h. multipliziere den Nenner und den Zähler mit . Dafür setzt du den Zähler und den Nenner auch in Klammern. | ||
| ↓ | Rechne das Produkt der zwei komplexen Zahlen im Zähler und das im Nenner aus. 4) Dafür multiplizierst du die Klammern erstmal wie gewohnt aus. | ||
| ↓ | Jetzt vereinfachst du den Zähler und den Nenner einzeln. Dafür rechnest du erstmal die Produkte aus. | ||
| ↓ | Verwenden, dass ist, um den Zähler und den Nenner noch weiter einzeln zu vereinfachen. Im Zähler hast du und im Nenner . | ||
| ↓ | Nun ordnest du Zähler und Nenner einzeln etwas: bringe die Zahlen ohne nach vorne und die Zahlen mit nach hinten. | ||
| ↓ | Wieder rechnest du im Zähler und Nenner erstmal einzeln, also getrennt: Nämlich verrechnest du jetzt die Zahlen ohne miteinander und die mit miteinander. | ||
| ↓ | 5) Jetzt hast du im Nenner eine reelle Zahl, nämlich nur noch die . 6) Nun teilst du jedes einzelne Glied vom Zähler durch diese Zahl im Nenner, also durch . | ||
| ↓ | Diese einzelnen Brüche vereinfachst du jetzt noch: | ||
Das ist das Endergebnis, da du nicht weiter vereinfachen kannst.
Teile durch .
1) Schreibe die Teilung als Bruch | |||
| ↓ | |||
| ↓ | Jetzt setzt du für und die komplexen Zahlen aus der Angabe ein: | ||
| ↓ | 2) Überlege dir die konjugiert Komplexe Zahl vom Nenner, also von . Ersetze das durch ein , um die konjugiert komplexe Zahl zu erhalten. Die konjugiert Komplexe ist also: 3) Nun erweiterst du den Bruch mit dieser Zahl, d.h. du multiplizierst den Nenner und den Zähler mit . Dafür setzt du den Zähler und den Nenner auch in Klammern. | ||
| ↓ | Jetzt rechnest du das Produkt der zwei komplexen Zahlen im Zähler und das im Nenner aus. 4) Dafür multiplizierst du die Klammern erstmal wie gewohnt aus. | ||
| ↓ | Jetzt kannst du den Zähler und den Nenner einzeln vereinfachen. Dafür rechnest du erstmal die Produkte aus. | ||
| ↓ | Jetzt verwendest du, dass ist, um den Zähler und den Nenner noch weiter einzeln zu vereinfachen. Im Zähler steht und im Nenner | ||
| ↓ | Nun verrechnest du alle Zahlen mit miteinander und alle Zahlen ohne | ||
| ↓ | 5) Jetzt steht im Nenner eine reelle Zahl, nämlich nur noch die 6) Nun teilst du jedes einzelne Glied vom Zähler durch diese Zahl im Nenner, also durch . Das Vorzeichen zwischen den Brüchen ist dasselbe, wie vorher oben auf dem Bruch stand. | ||
| ↓ | Die Brüche kannst du noch kürzen. | ||
Das ist das Endergebnis. Du hast eine komplexe Zahl der Form erhalten, mit und .
Darstellung komplexer Zahlen im Koordinatensystem
Der Betrag einer komplexen Zahl lässt sich genauso berechnen, wie die Länge eines Vektors. Du kannst dir eine komplexe Zahl also als zweidimensionalen Vektor vorstellen, der die -Komponente und die -Koordinate hat:
Wenn du diesen Vektor in ein Koordinatensystem einzeichnen willst, gehst du Einheiten entlang der -Achse und anschließend Einheiten entlang der -Achse.
Analog kann man eine komplexe Zahl in ein Koordinatensystem einzeichnen. Auf der -Achse wird der Realteil aufgetragen. Deswegen wird diese Achse statt mit nun mit für den Realteil beschriftet. Auf der -Achse wird der Imaginärteil aufgetragen. Deswegen wird diese Achse mit beschriftet. Diese -Ebene nennt man die Gaußsche Zahlenebene.
So kann man jede komplexe Zahl in einem fast gewöhnlichen Koordinatensystem als Vektor darstellen.
In diesem Applet kannst du den blauen Punkt verschieben. Er steht für die komplexe Zahl . Wenn du ihn horizontal, also entlang der -Achse verschiebst, ändert sich der Realteil. Wenn du den Punkt vertikal, also entlang der -Achse verschiebst, ändert sich der Imaginärteil.
Du kannst außerdem den Betrag und die konjugiert komplexe Zahl einblenden. Der Betrag hat eine geometrische Bedeutung: Er ist der Abstand der komplexen Zahl vom Ursprung.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
