2019-06-04 Beispiel der Legendre-Transformation in der Mikroökonomie

Über die Legendre-Transformation kann möglicherweise der Lagrange-Formalismus verstanden werden. Schließlich ist die Langrange-Funktion $L$ die Legendre-Transformation der Hamilton-Funktion. Ein Beispiel aus der Wirtschaft soll verdeutlichen, wie man sich die Legendre-Transformation vorstellen kann.

Wir haben eine Fabrik, die eine Anzahl $Q$ an Güter innerhalb einer Woche produzieren soll. Die Kosten pro Gut $K$ , die bei der Produktion entstehen, steigt mit der Anzahl der Güter, die pro Woche produziert werden sollen. So müssen bei steigender Anzahl die Arbeiterinnen und Arbeiter mehr Lohn wegen größeren Arbeitszeiten erhalten. Irgendwann fallen auch Sonderzahlungen an oder neue Maschinen müssen gekauft werden. So ist der Graph, der die aktuellen Kosten pro Gut $K$ zur aktuellen Zahl der produzierten Güter $G$ angiebt, eine streng monotone Funktion:

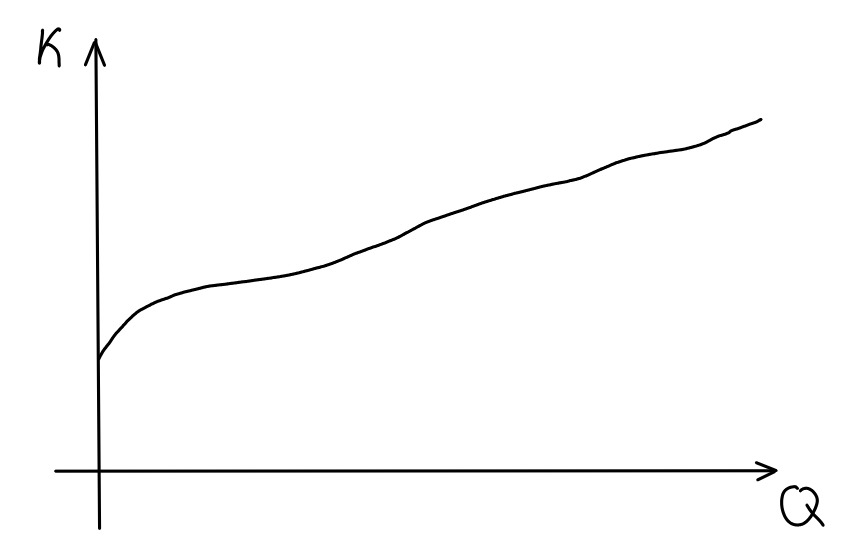
Das Integral $\int_0^Q K(\tilde Q)\,\mathrm d\tilde Q$ gibt die Gesamtkosten an, die wir als Unternehmen für die Produktion von $Q$ Gütern bezahlen müssen. Sei der Weltmarktpreis für unser Gut $K_W$ und $\hat Q$ sei die Zahl der Güter, die wir produziert haben. Wenn wir diese verkaufen, machen wir $K_W\cdot \hat Q$ Umsatz und damit einen Gewinn von $K_W\cdot \hat Q - \int_0^{\hat Q} K(\tilde Q)\,\mathrm d\tilde Q$ :

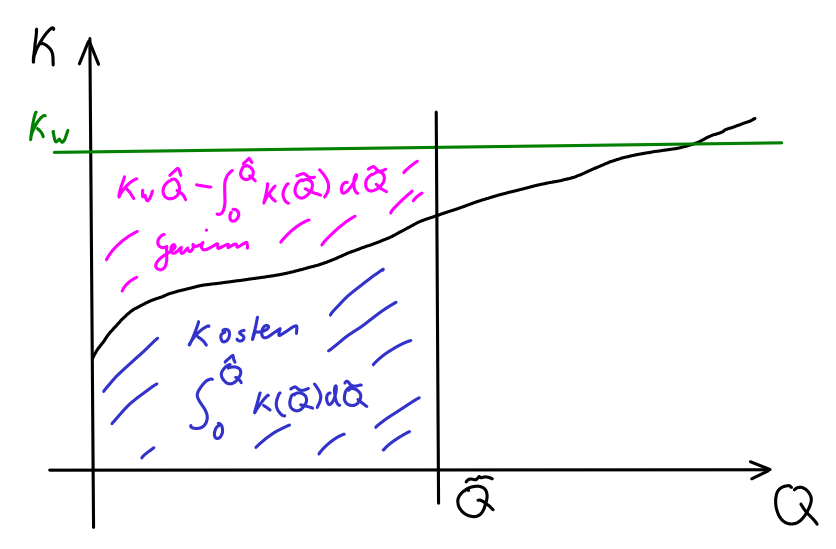
Wie viele Güter sollen wir produzieren, damit unser Gewinn maximal ist? Solange der aktuelle Weltmarktpreis größer als unsere aktuellen Kosten ist ( $K_W > K(Q)$ ), machen wir zusätzlichen Gewinn, wenn wir weitere Güter produzieren. Bei $K_W < K(Q)$ machen wir durch die Produktion weiterer Güter Verlust? Wenn wir nämlich $\mathrm dQ$ an neuen Gütern produzieren, so ist $K_W\cdot \mathrm dQ - K(Q)\cdot \mathrm dQ$ der erzielte Gewinn durch den Verkauf der $\mathrm dQ$ an neuen Gütern:

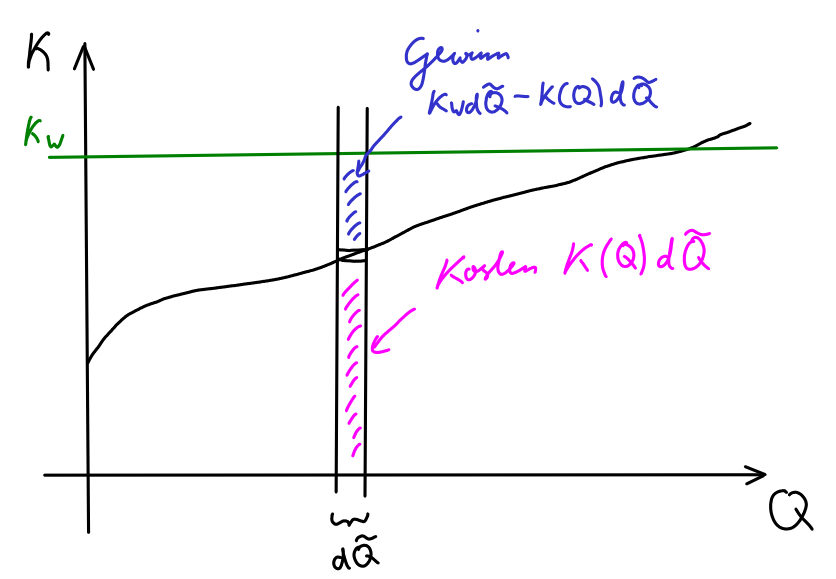
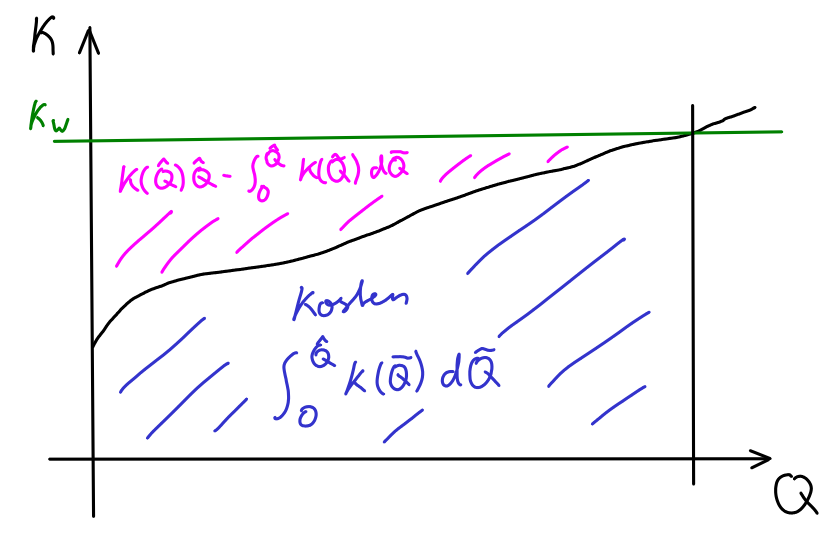
Die optimale Anzahl an zu produzierenden Gütern ist diejenige Anzahl $\hat Q$ , bei der $K_W = K(\hat Q)$ ist. Dann ist der gemachte Gewinn $G$ die Legendre-Transformation von unseren Kosten:

\displaystyle G=K(\hat Q)\cdot \hat Q - \int_0^{\hat Q} K(\tilde Q)\,\mathrm d\tilde Q

Es ist:

Offene Fragen

Kann das obige Beispiel im Fall des Lagrange-Formulismus angewandt werden, um die Lagrange-Funktion $L=p\cdot \dot q - H$ zu verstehen? So ist es möglich den Impuls $p$ als „Kosten“ zu interpretieren. Wenn nämlich ein Körper die Geschwindigkeit $\dot q$ und den Impuls $p(\dot q)$ hat, so ist $p(\dot q)\cdot \mathrm d\dot q$ die Energie, die aufgewendet werden muss, um die Geschwindigkeit um $\mathrm d\dot q$ zu erhöhen. Wie kann aber $p\cdot \dot q$ interpretiert werden? Was gibt dieser Term an?

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Quellen

Abschnitt „Microeconomics“ im englischsprachigen Wikipedia-Artikel „Legendre transformation“ (Zugriff 2019-06-07)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?