Artikel in Arbeit…

Der elektrische Widerstand ist eine physikalische Größe, die den Zusammenhang zwischen der Spannung am Leiter und der Stromstärke im Leiter beschreibt.
Der Widerstand ist eine Eigenschaft des Materials, aus dem der Leiter hergestellt ist. Für manche Stoffe gilt das Ohmsche Gesetz:
Demnach ist der Widerstand der Quotient aus Spannung und Stromstärke.
Gilt bei einem bestimmten Stoff das Ohmsche Gesetz, ist die Stromstärke proportional zu der Spannung:
Zusammenhang zwischen Spannung und Stromstärke
Zur Veranschaulichung kann ein Versuchsaufbau wie in Abb. 1 dienen.
In einem Stromkreis mit veränderbarer Spannung befindet sich ein Leiter, zum Beispiel Eisen.
Die Spannung wird zunächst auf eine bestimmte Größe eingestellt und der Wert der Stromstärke abgelesen.
Nun wird die Spannung erhöht und erneut die Stromstärke gemessen.
Die Werte werden in einem Diagramm wie in Abb. 2 eingetragen.
Die gemessenen Punkte ergeben die Kennlinie des Widerstands bzw. die U-I-Kennlinie.
Zum Vergleich kann der Versuch mit anderen Stoffen wiederholt werden, zum Beispiel Grafit und Konstanten.
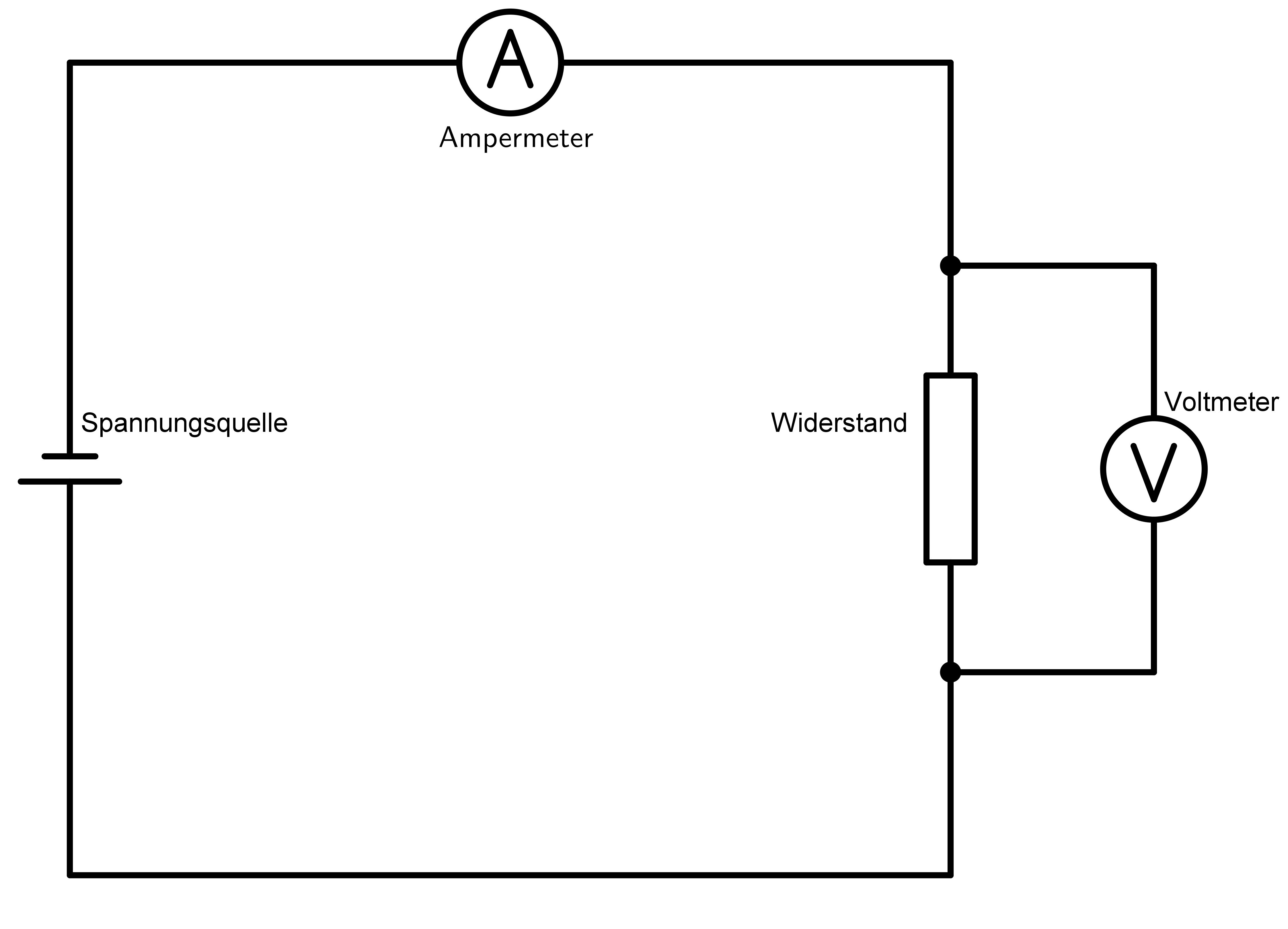
Abb. 1: Versuchsaufbau
Beobachtung
Mit zunehmender Spannung erhöht sich in allen drei Fällen die Stromstärke.
Bei Grafit nimmt die Stromstärke schneller zu und bei Eisen langsamer.
Für Konstantan erhält man eine Ursprungsgerade. Die Spannung ist proportional zur Stromstärke.
Für Konstantan gilt das Ohmsche Gesetz. Der Widerstand bleibt konstant.

Abb. 2: Diagramm schematisch. Rot: Eisen, Grün: Konstanten, Blau: Grafit
Widerstand eines Leiters
In elektrischen Leitern, z. B. Metallen, drängen sich die Elektronen zwischen den Metallatomen durch. Durch Stöße mit den Atomen verlieren die Elektronen an Energie und das Strömen wird behindert. Es kann vorkommen, dass in einem Metall an einzelnen Stellen fremde Atome sitzen, z. B. Kohlenstoff in einem Eisendraht, oder dass an einigen Stellen Atome fehlen. Solche Defekte beeinflussen das Strömen der Elektronen.
Man kann also sagen, dass der Leiter dem Strom einen Widerstand entgegensetzt. Dieser wird auch als elektrischer Widerstand bezeichnet.
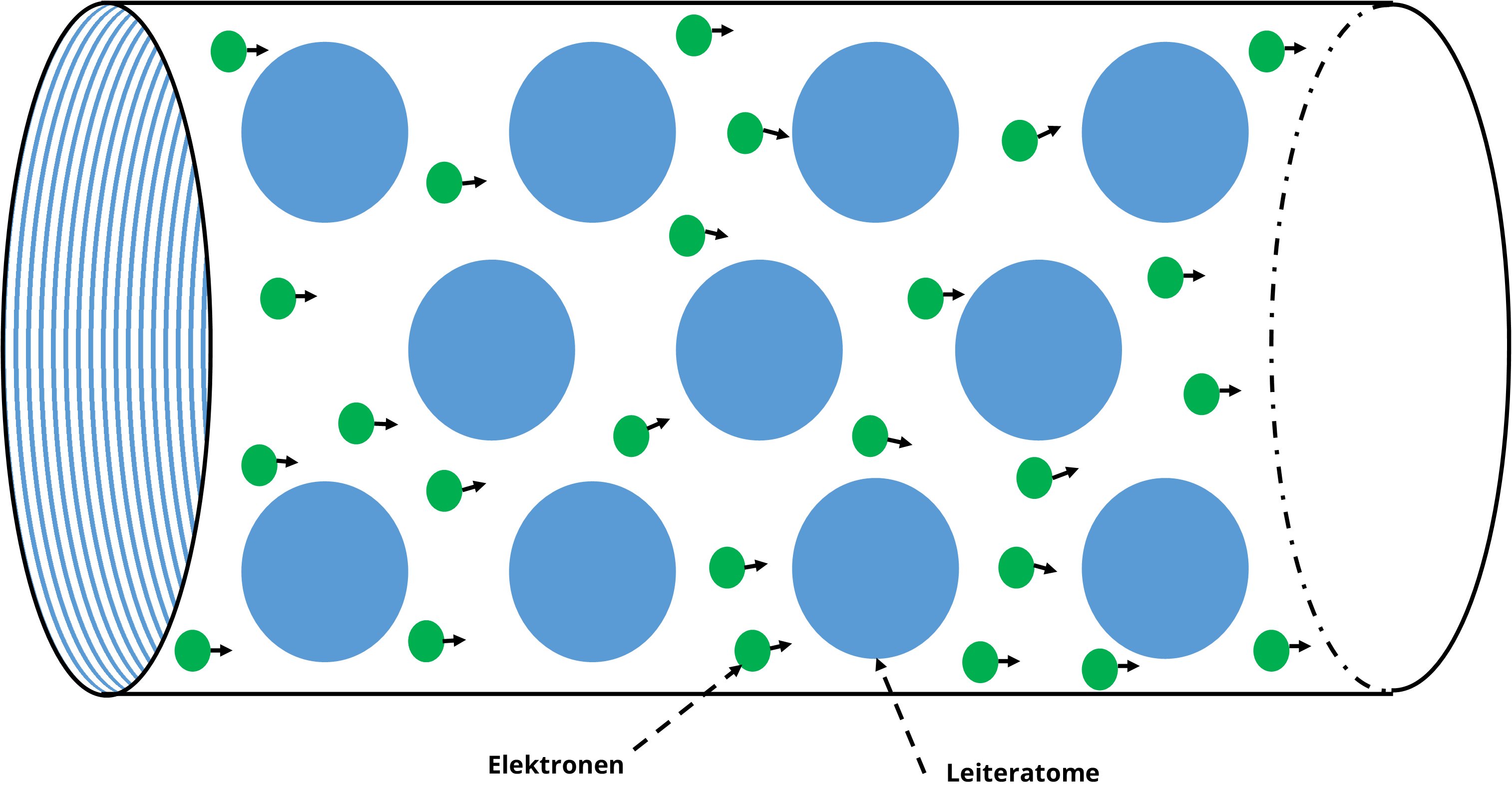
Abb. 3: Widerstand im Leiter
Auch die Temperatur hat einen Einfluss: Die Atome im Leiter sitzen nicht fest in einem starren Gitter, sondern wirbeln um ihren Platz herum, umso schneller, je wärmer es ist. In den meisten Metallen steigt deshalb der Widerstand mit der Temperatur.
Doch was passiert mit der Energie der Elektronen? Sie wird in Wärmeenergie umgewandelt. Diesen Effekt kennt man aus dem Alltag. So ist dies zum Beispiel die Funktion der alten Glühbirne oder einer Herdplatte. Der Wolframdraht der Glühlampe erwärmt sich durch den Widerstand des Drahtes.

Abb. 4: Glühbirne und Herdplatte
Beim Betrachten des Models mit den Elektronen, die sich zwischen den Metallatomen „durchzwängen“, wird auch die Beobachtung aus dem Versuch nachvollziehbar, dass verschiedene Materialien unterschiedliche Widerstände besitzen. Die Metalle haben unterschiedliche Atomdichten, unterschiedlich viele freie Elektronen pro Atom usw.
Was hätte man gemessen, wäre in dem Versuch eine dickere Leitung verwendet worden? Das würde bedeuten, dass der Querschnitt größer wäre und somit mehr Elektronen auf einmal fließen könnten. Mehr Elektronen (Ladung) pro Zeit bedeuten eine höhere Stromstärke. Laut der Formel wäre der Widerstand bei gleicher Spannung also niedriger. Was ist, wenn das Kabel länger ist? Dann müssten die selben Elektronen eine längere Strecke zurücklegen und dabei an viel mehr Atomen vorbeikommen. Sie werden also stärker ausgebremst.
Tatsächlich hängt der Gesamtwiderstand eines Leiters von dessen Geometrie ab, sowie von einem stoffspezifischen Widerstand des Materials.
Spezifischer Widerstand
Der spezifische Widerstand ist eine stoffbezogene Konstante. Nach Definition ist er der Wert des Widerstandes eines 1 m langen Leiters mit dem Querschnitt 1 mm² bei 20°. Somit gilt für den „tatsächlichen“ Widerstand eines Leiterstücks: mit die Länge des Leiters, die konstante Querschnittsfläche und (rho) dem spezifischen Widerstand.
Formeln und Berechnungen
Kategorie | Formeln und Einheiten | Bemerkungen |
|---|---|---|
Formelzeichen |
| |
SI- Einheit |
| |
Formel |
| Spannung durch Stromstärke (Merkhilfe: "Rudi" für ist durch ) |
| Spezifischer Widerstand mal Länge durch Querschnittsfläche. |
Schaltsymbol
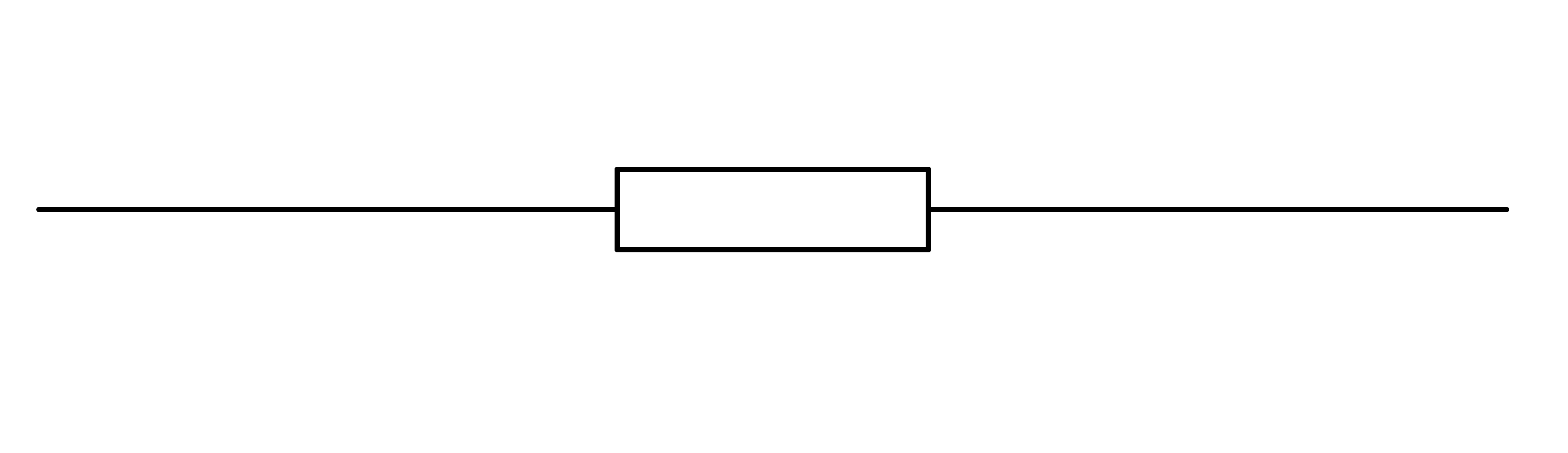
Abb. 5: Ohmscher Widerstand
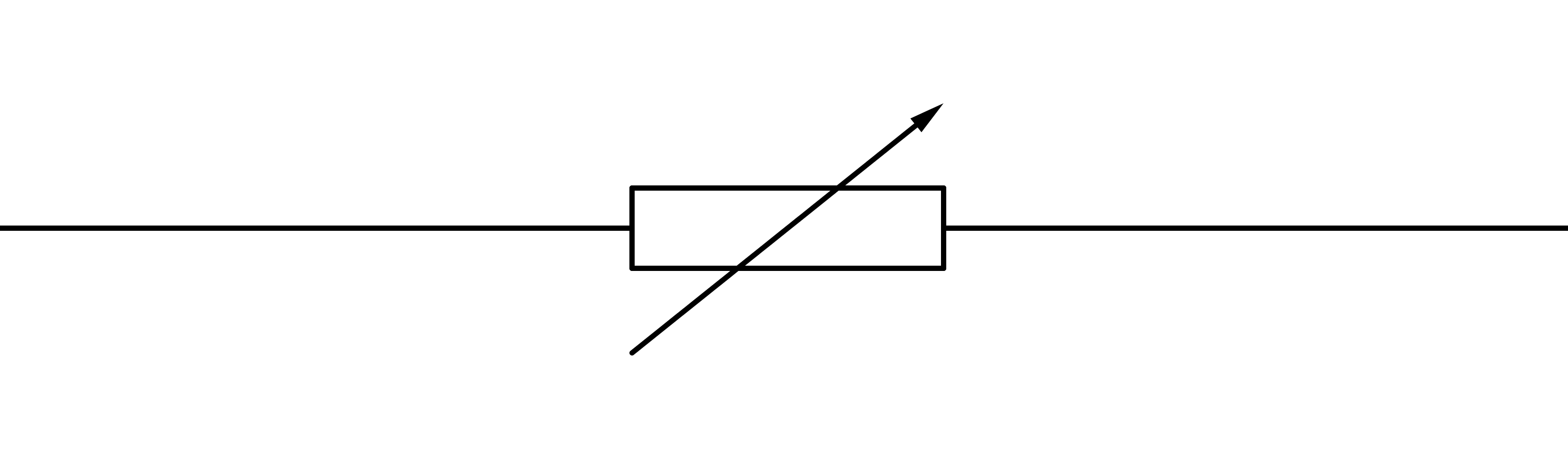
Abb. 6: Regelbarer Widerstand
