Limes-Schreibweise

1 Überblick

Die folgenden Seiten helfen dir, zu verstehen, wofür die Limes-Schreibweise gut ist und wie sie aufgebaut ist.

Kursdauer: ca 10-15 Minuten

2 Graphen skizzieren

Lynn und Finn haben in Mathe die Hausaufgabe bekommen, die Graphen verschiedener Funktionen zu skizzieren. Am Nachmittag telefonieren sie, um ihre Lösungen zu vergleichen.

Lynn: "Also ich fang oben an zu zeichnen"

Finn: "Halt, warte! Oben links oder oben rechts?"

Lynn: "Oben links. Und dann gehe ich durch die Nullstellen, wie wir es gelernt haben und komme dann unten raus"

Finn: "Also insgesamt von links oben nach rechts unten?"

Lynn: "Genau."

Was Lynn und Finn gerade umgangssprachlich besprochen haben, ist der Globalverlauf einer Funktion. Während dieser mündlich durchaus so beschrieben werden kann, geht es schriftlich weitaus kompakter und präziser.

Um Grenzwerte, wie zum Beispiel den Verlauf im Unendlichen, schnell, einheitlich und kompakt zu beschreiben, verwendet man in der Mathematik deshalb die Limes-Schreibweise.

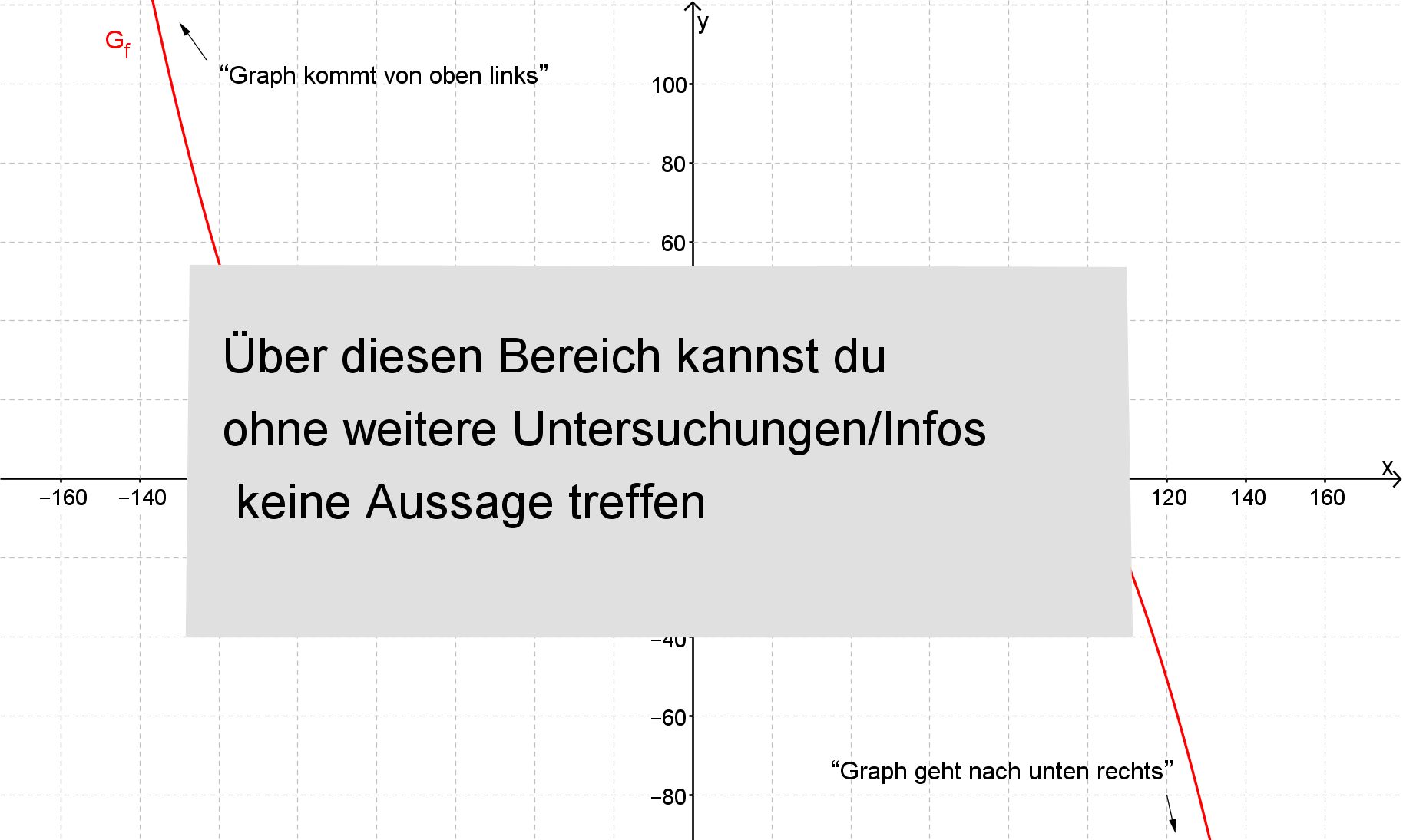
3 Erster Kontakt zur Limes-Schreibweise

Die Limes-Schreibweise besteht aus drei Komponenten, die du auf den nächsten Folien alle einzeln kennenlernen wirst.

Insgesamt sieht die Schreibweise für "Der Graph der Funktion f kommt von links oben" so aus:

\displaystyle \lim_{x\to-\infty}f(x)=+\infty

Und wenn du ausdrücken möchtest, dass der Graph nach rechts unten verschwindet, schreibst du das folgendermaßen:

\displaystyle \lim_{x\to \infty}f(x)=-\infty

Meistens ist es deine Aufgabe, die rechte Seite zu ermitteln, so dass du dir erstmal nur den linken Teil anschauen musst.

4 Anweisung "lim"

\displaystyle \underset{ x\to \infty}{\color{red}\lim}f(x)

Die Buchstaben "lim" stehen für Limes, was lateinisch für Grenze ist.

Sie sagen aus, dass das Verhalten an der "Grenze" (siehe nächste Seite) beschrieben werden soll.

Der Limes ist also so etwas wie eine Aufforderung, ein festes Signalwort: "Untersuche, wie sich die Funktionswerte verhalten, wenn du an die angegebene Grenze gehst."

5 Grenze

\displaystyle \underset{\color{red}x\to \infty}{\lim}f(x)

Unter die Anweisung " $\text{lim}$ " schreibst du die Grenze, die untersucht werden soll, also auf die das $x$ (oder eine andere Variable) zuwandert.

Dass das $x$ sich dieser Grenze nähern soll, signalisierst du durch einen Pfeil.

Beispiele:

$x\to +\infty$ : Das $x$ soll sehr große positive Werte (100, 1000, 10000,...) annehmen. Man spricht " $x$ gegen plus-unendlich". Graphisch wird dadurch der Verlauf des Graphen am rechten Rand des Koordinatensystems erfragt.

$x\to -\infty$ : Das $x$ soll sehr große negative Werte annehmen. Man spricht " $x$ gegen minus-unendlich". Graphisch wird dadurch der Verlauf des Graphen am linken Rand des Koordinatensystems erfragt.

6 Argument

\displaystyle \lim_{x\to \infty}{\color{red}f(x)}

Während die Grenze gesagt hat, wohin das $x$ wandern soll, besagt das Argument in was das $x$ dabei eingesetzt wird.

Meistens ist das Argument eine Funktion. Der Limes wird hierbei verwendet, um zu untersuchen, wie die Funktionswerte sich verhalten, wenn das $x$ bestimmte Werte annimmt: Werden die Funktionswerte sehr große positive Zahlen oder sehr große negative Zahlen oder nähern sie sich gar einem bestimmten Wert?

Statt $f (x)$ kannst du auch direkt den Funktionsterm schreiben. Zum Beispiel für $f (x) = x^{2} + x$

\displaystyle \lim_{x\to -\infty}(x^2+x)

7 Bestimmung des Grenzwertes

Häufig ist es deine Aufgabe, einen Grenzwert zu bestimmen. Wie du das machst, ist sehr unterschiedlich und hängt beispielsweise davon ab, um was für eine Funktion es sich im Argument handelt und ob deine Grenze $\pm\infty$ oder eine Zahl oder gar Variable ist.

Wenn du die Limes-Schreibweise verstanden hast, kann dir bei Funktionen aber manchmal der Taschenrechner einen Eindruck vermitteln, wie der Grenzwert aussehen kann.

BeispielGrenzwert im Unendlichen

Bestimme $\lim\limits_{x\to +\infty}2^x$ und $\lim\limits_{x\to -\infty}2^x$ .

(Du kannst diese Aufgabe mithilfe des Taschenrechners auch lösen, wenn du die Funktionsart Exponentialfunktion noch nicht kennst!)

Setze in den Taschenrechner sehr große positive und negative Zahlen für x in $f (x) = 2^{x}$ ein und überprüfe, wie sich die Werte entwickeln:

$\lim\limits_{x\to +\infty}2^x$ :

$f(10)=2^{10}=1024$

$f(11)=2^{11}=2048$

$f(100)=2^{100}\approx1{,}2\cdot 10^{30}$

Die Funktionswerte werden immer größer, also $\lim\limits_{x\to +\infty}2^x=+\infty$

$\lim\limits_{x\to-\infty}2^x$ :

$f(-10)=\frac 1{1024}\approx 0{,}001$

$f(-11)=\frac 1{2048}\approx0{,}0005$

$f(-100)=\frac 1{2^{100}}\approx 0{,}0000...1$

Die Funktionswerte nähern sich immer näher an die 0, also $\lim\limits_{x\to-\infty}2^x=0$

Ohne weiteres Wissen über Nullstellen oder Extrempunkte könnte der Graph also so aussehen (und tut es auch!):

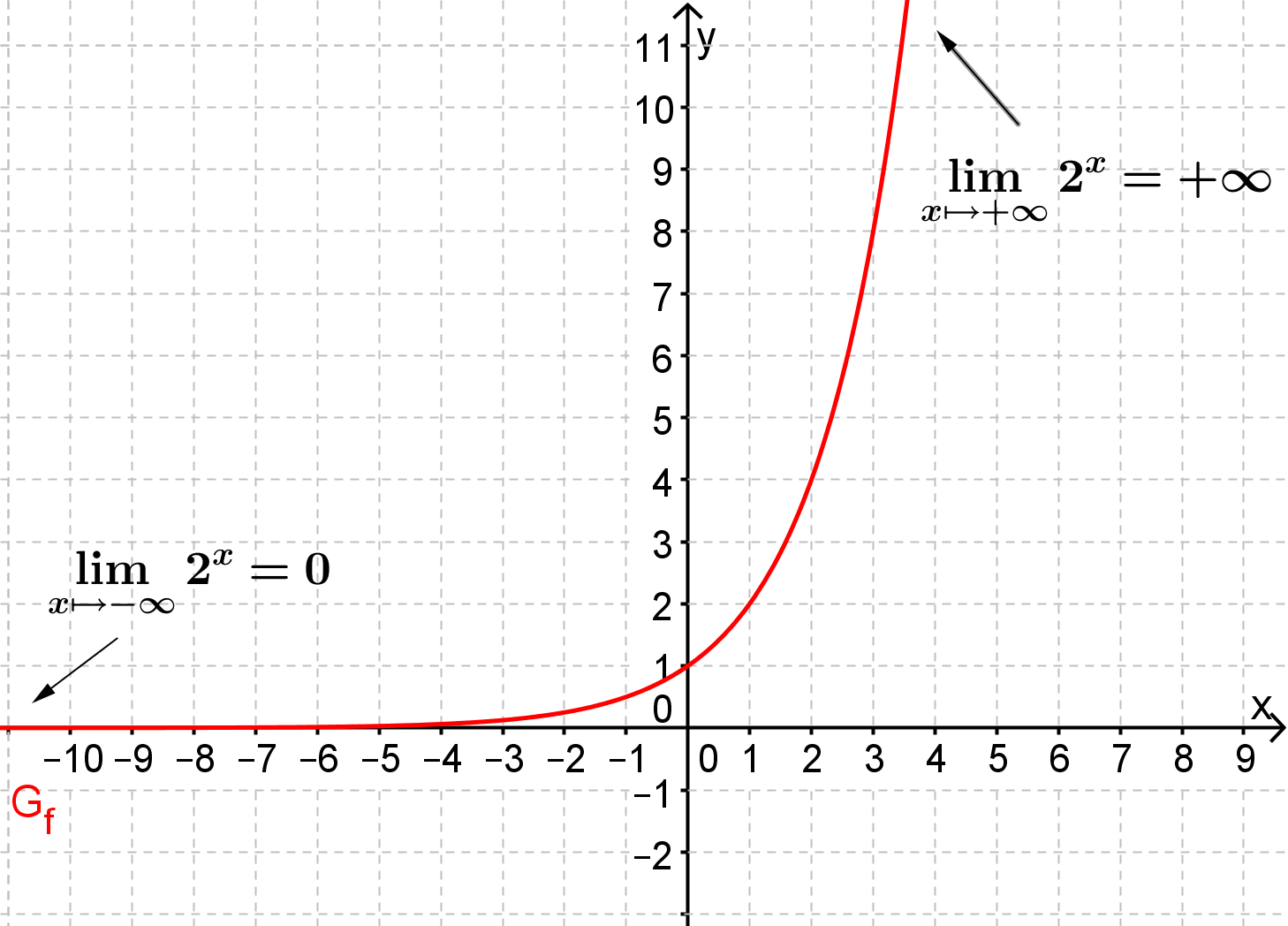
8 Übungen

Laden