Aufgabenstellung

$2.$ Nach einer aktuellen Erhebung leiden $25$ % der Einwohner Deutschlands an einer Allergie. Aus den Einwohnern Deutschlands werden $n$ Personen zufällig ausgewählt.

$a$) Bestimmen Sie, wie groß $n$ mindestens sein muss, damit mit einer Wahrscheinlichkeit von mehr als $99$ % mindestens eine der ausgewählten Personen an einer Allergie leidet. (4 BE)

Lösung

Du entnimmst aus der Aufgabenstellung, dass $X$ die Wahrscheinlichkeitsfunktion $B(200;\mathrm{0,25})$ hat.

Du sollst nun die Wahrscheinlichkeit berechnen, dass $X$ höchstens um eine Standardabweichung ${\sigma }_X$ vom Erwartungswert $E(X)$ abweicht. Mathematisch ausgedrückt:

Erwartungswert und Standardabweichung bestimmen

Für den Erwartungswert einer binomialverteilten Zufallsgröße $Y$ gilt $E(Y)=n\cdot p$. Es folgt:

Für die Standardabweichung einer binomialverteilten Zufallsgröße $Y$ gilt ${\sigma }_Y=\sqrt{np(1-p)}$. Es folgt:

${\sigma }_X=\sqrt{200\cdot \mathrm{0,25}\cdot \mathrm{0,75}}=\sqrt{\mathrm{37,5}}\approx \mathrm{6,1}$

Wahrscheinlichkeit ausrechnen

Du formst jetzt $P(|X-E(X)|\le {\sigma }_X)$ um, so dass du das Tafelwerk verwenden kannst.

Es gilt:

$P(|X-E(X)|\le {\sigma }_X)=P(-{\sigma }_X+E(X)\le X\le {\sigma }_X+E(X))=P(X\le {\sigma }_X+E(X))-P(X<E(X)-{\sigma }_X)$

Mit eingesetzten Werten also:

$P(X\le \mathrm{56,1})-P(X<\mathrm{43,9})=P(X\le 56)-P(X\le 43)=\mathrm{0,8555}-\mathrm{0,1438}\approx \mathrm{0,71}$.

Antwort: Die Wahrscheinlichkeit beträgt $71$ Prozent.

Aufgabenstellung

$3.$ Ein Pharmaunternehmen hat einen Hauttest zum Nachweis einer Tierhaarallergie entwickelt. Im Rahmen einer klinischen Studie zeigt sich, dass der Hauttest bei einer aus der Bevölkerung Deutschlands zufällig ausgewählten Person mit einer Wahrscheinlichkeit von $\mathrm{39,5}$ % ein positives Testergebnis liefert. Leidet eine Person an einer Tierhaarallergie, so ist das Testergebnis mit einer Wahrscheinlichkeit von $85$ % positiv. Das Testergebnis ist jedoch bei einer Person, die nicht an einer Tierhaarallergie leidet, mit einer Wahrscheinlichkeit von $35$ % ebenfalls positiv.

Lösung

Das Stichwort zu dieser Aufgabe ist das Baumdiagramm.

Zunächst musst du dir überlegen, welche beiden Ereignisse hier betrachtet werden. Man liest aus dem Text:

$A:$ Person leidet an Tierhaarallergie.

$B:$ Hauttest liefert positives Testergebnis.

Erstelle nun ein Baumdiagramm und trage die Wahrscheinlichkeiten aus dem Text dort ein.

$P(B)=\mathrm{0,395}$

$P_A(B)=\mathrm{0,85}$

$P_{\overline{A}}(B)=\mathrm{0,35}$

$P(A)=p$

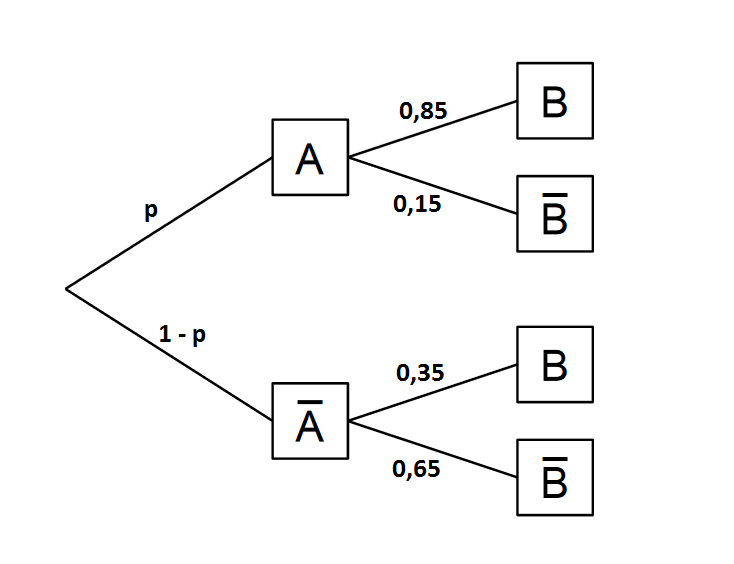
Du möchtest den Wert $p$ der Wahrscheinlichkeit $P(A)$ berechnen. Verwende dafür die zweite Pfadregel:

Aus dem Baumdiagramm kannst du dir die relevanten Wahrscheinlichkeiten rauslesen. Es folgt:

Stelle noch nach $p$ um. Du erhältst:

Antwort: Die Anteil der Bevölkerung mit Tierhaarallergie beträgt $9$ Prozent.

Aufgabenstellung

$3.$ Ein Pharmaunternehmen hat einen Hauttest zum Nachweis einer Tierhaarallergie entwickelt. Im Rahmen einer klinischen Studie zeigt sich, dass der Hauttest bei einer aus der Bevölkerung Deutschlands zufällig ausgewählten Person mit einer Wahrscheinlichkeit von $\mathrm{39,5}$ % ein positives Testergebnis liefert. Leidet eine Person an einer Tierhaarallergie, so ist das Testergebnis mit einer Wahrscheinlichkeit von $85$ % positiv. Das Testergebnis ist jedoch bei einer Person, die nicht an einer Tierhaarallergie leidet, mit einer Wahrscheinlichkeit von $35$ % ebenfalls positiv.

$a$) Ermitteln Sie, welcher Anteil der Bevölkerung Deutschlands demnach allergisch auf Tierhaare reagiert. (4 BE)

Lösung

Gesucht ist die Wahrscheinlichkeit von Ereignis $A$ für den Fall, dass Ereignis $B$ schon eingetreten ist. In mathematischer Schreibweise ausdrückt also die bedingte Wahrscheinlichkeit $P_B(A)$.

Nun gilt per Definition für bedingte Wahrscheinlichkeiten folgende Beziehung:

Aus dem Baumdiagramm der vorherigen Aufgabe lässt sich $P(B\cap A)$ einfach ausrechnen. $P(B)$ ist bereits bekannt. Es folgt:

Antwort: Die Wahrscheinlichkeit, dass eine positiv getestete Person tatsächlich an einer Tierallergie leidet, beträgt ungefähr $19$ Prozent.

Aufgabenstellung

$3.$ Ein Pharmaunternehmen hat einen Hauttest zum Nachweis einer Tierhaarallergie entwickelt. Im Rahmen einer klinischen Studie zeigt sich, dass der Hauttest bei einer aus der Bevölkerung Deutschlands zufällig ausgewählten Person mit einer Wahrscheinlichkeit von 39,5 % ein positives Testergebnis liefert. Leidet eine Person an einer Tierhaarallergie, so ist das Testergebnis mit einer Wahrscheinlichkeit von 85 % positiv. Das Testergebnis ist jedoch bei einer Person, die nicht an einer Tierhaarallergie leidet, mit einer Wahrscheinlichkeit von 35 % ebenfalls positiv.

$a)$ Ermitteln Sie, welcher Anteil der Bevölkerung Deutschlands demnach allergisch auf Tierhaare reagiert. (4 BE)

$b)$ Eine aus der Bevölkerung Deutschlands zufällig ausgewählte Person wird getestet; das Testergebnis ist positiv. Berechnen Sie die Wahrscheinlichkeit dafür, dass diese Person tatsächlich an einer Tierhaarallergie leidet. (2 BE)

Lösung

Betrachte die linke und rechte Seite des Terms $\mathrm{0,09}\cdot \mathrm{0,15}+\mathrm{0,91}\cdot \mathrm{0,35}$ zunächst seperat.

Es ist in diesem Fall hilfreich, das Baumdiagramm aus der Teilaufgabe $a)$ zu verwenden.

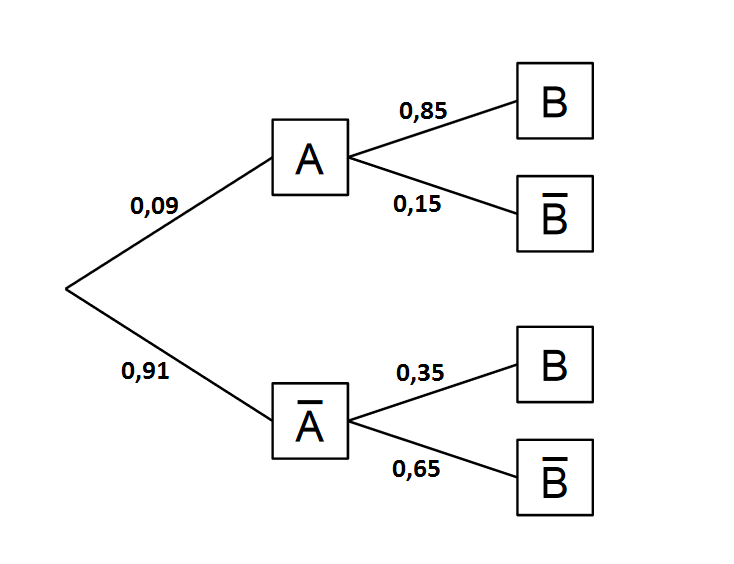
linker Term

Die linke Seite des Terms entspricht laut Baumdiagramm dem Ereignis $A\cap \overline{B}$.

Interpretation: Eine Person leidet an einer Tierallergie und hat ein negatives Testergebnis.

rechter Term

Die rechte Seite des Terms entspricht laut Baumdiagramm dem Ereignis $\overline{A}\cap B$:

Interpretation: Eine Person leidet nicht an der Tierallergie und hat ein positives Testergebnis.

gesamter Term

Die Summe der beiden Terme entspricht also dem Ereignis $(A\cap \overline{B})\cup (\overline{A}\cap B)$.

Interpreation: Eine Person erhält ein falsches Testergebnis.