7Lösung 3b

Aufgabenstellung

$33$Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion $f:x\mapsto \sqrt{25-x^2}f:\; x\backslash mapsto\; \backslash sqrt\{25-x^2\}$ mit Definitionsbereich $D_f=[-5;5]D\_f=[-5;5]$.

$a)a)$ Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte M den Abstand $5m5\; m$ hat. Zeichnen Sie den Graphen von f in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: $5\le x\le 95\backslash le\; x\backslash le\; 9$, $1\le y\le 131\backslash le\; y\backslash le\; 13$) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist. (5 BE)

Betrachtet wird nun die Integralfunktion $F:x\mapsto {\int }_0^{x}f(t)dtF:\; x\backslash mapsto\; \backslash int\_\{0\}^\{x\}\; f(t)\; dt$ mit Definitionsbereich $D_F=[-5;5]D\_F=[-5;5]$.

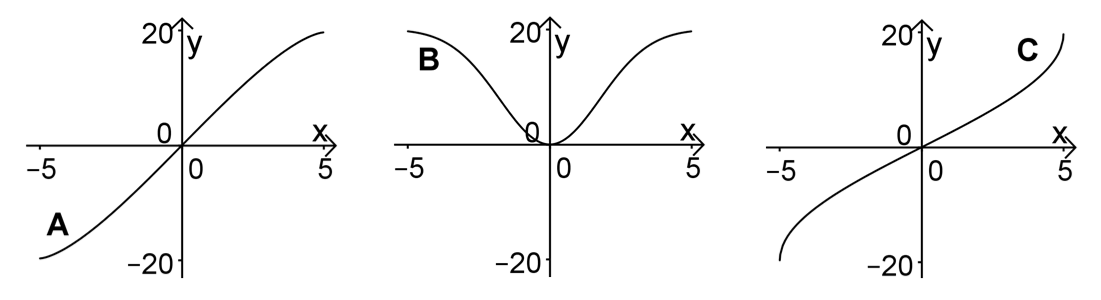
Zeigen Sie mithilfe einer geometrischen Überlegung, dass $F(5)=\frac{25}{4}\pi F(5)=\backslash frac\{25\}\{4\}\backslash pi$ gilt. Einer der Graphen A, B und C ist der Graph von F. Entscheiden Sie, welcher dies ist, und begründen Sie Ihre Entscheidung, indem Sie erklären, warum die beiden anderen Graphen nicht infrage kommen. (5 BE)

Lösung

$F(5)=\frac{25}{4}\pi F(5)=\backslash frac\{25\}\{4\}\backslash pi$

Überlege dir zuerst, wofür $F(5)F(5)$ steht

$F(5)=F:x\mapsto {\int }_0^{5}f(t)dtF(5)=F:\; x\backslash mapsto\; \backslash int\_\{0\}^\{5\}\; f(t)\; dt$

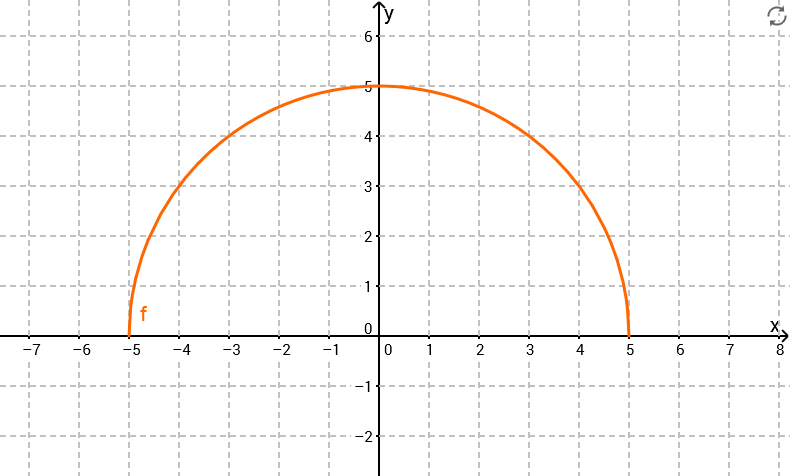
$F(5)F(5)$ steht also für die Fläche unter dem Graphen von $x=0x=0$ bis $x=5x=5$. Wie man an dem Graphen von 3a sehen kann, handelt es sich dabei um einen Viertelkreis mit Radius $5m5m$. Berechne den Flächeninhalt.

$F(5)=\frac{1}{4}\cdot 5^2\pi =\frac{25}{4}\pi F(5)=\backslash frac\{1\}\{4\}\backslash cdot\; 5^2\backslash pi=\backslash frac\{25\}\{4\}\backslash pi$

Damit ist das Kontrollergebnis bestätigt.

Auswahl des richtigen Graphen

Man könnte sich zuerst überlegen, ob die Funktion $F(x)F(x)$ links des Ursprungs positiv oder negativ sein muss.

Sie muss negativ sein, weil die Fläche zwar oberhalb der $xx$-Achse ist, aber man in negative Richtung integriert. Damit scheidet der Graph B aus, weil hier die Funktion links des Ursprungs positiv ist.

Also kommen nur noch die Graphen A und C in Frage. Bei Graph A ist der Flächenzuwachs erst groß und wird dann abgeschwächt, bei Graph C ist es umgekehrt. Überlege, was zutrifft.

Bei einem Kreis ist die Fläche um den Ursprung mehr als am Rand (siehe Graph 3a), das heißt, dass der Flächenzuwachs am Anfang groß ist und dann abnimmt.

Damit ist Graph A richtig und Graph C falsch.