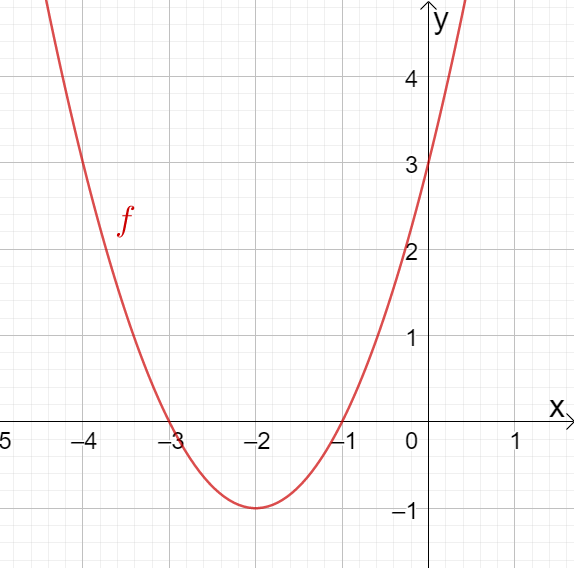
Gegeben ist der nebenstehende Graph der Funktion . Bestimme die Funktionsgleichung in Nullstellenform.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenform
Bestimmung der Nullstellenform
Verwende das Vorgehen aus dem Artikel Nullstellenform zur Bestimmung der Nullstellenform:
Zuerst musst du die Nullstellen des Graphen bestimmen.
Du siehst vielleicht, dass eine Nullstelle bei existiert und eine weitere bei . Die Vielfachheit ist jeweils . Falls du hier Probleme hast, schau nochmal in den Artikel zu Nullstellen.
Die Funktion hat also zwei unterschiedliche Nullstellen der Vielfachheit . Dies entspricht dem 1. Fall des Vorgehens aus dem Artikel über die Nullstellenform.
Die Funktionsgleichung ist also von der Form:
mit dem Öffnungsfaktor .
Als Nächstes ist zu bestimmen. Dafür gibt es zwei verschiedene Varianten:
1. Variante
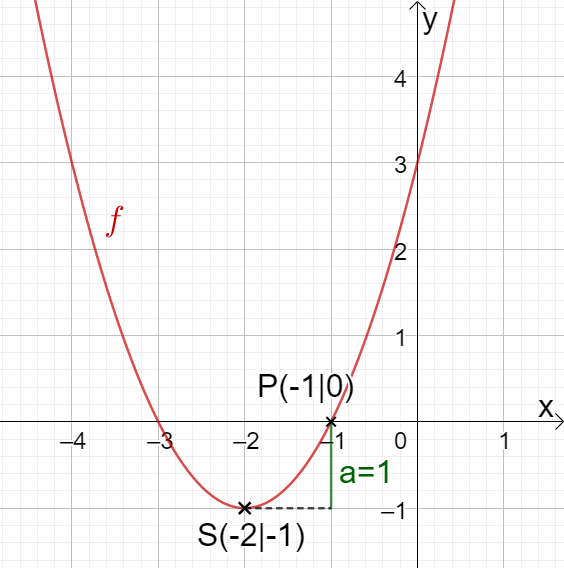
Der Öffnungsfaktor kann ausgehend vom Scheitelpunkt und dem Punkt abgelesen werden.
Du erhältst .
Die Nullstellenform der Funktion lautet also:
.
2. Variante
Die Nullstellenform ist, abgesehen von , bereits gefunden. Sie lautet:
Setzt du jetzt einen Punkt ein, der auf dem Graphen liegt, aber keine Nullstelle ist, so kannst du die Gleichung nach auflösen.
Du kannst am Graphen sehen, dass der Punkt auf diesem liegt und keine Nullstelle ist. Setze also in die Funktionsgleichung ein und löse nach auf.
Teilst du beide Seiten der Gleichung durch , erhältst du .
Damit ist die Nullstellenform gegeben durch:
.
Erinnere dich an das im Artikel Nullstellenform beschriebene Schema zur Bestimmung der Nullstellenform.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
