Berechne die Fläche der Dreiecke .
- FE
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreiecksfläche berechnen
Skizziere die Punkte und das Dreieck in ein Koordinatensystem ein, um einen Überblick zu erhalten. Wähle eine Ecke, von der die Vektoren das Dreieck aufspannen, und berechne diese Vektoren.
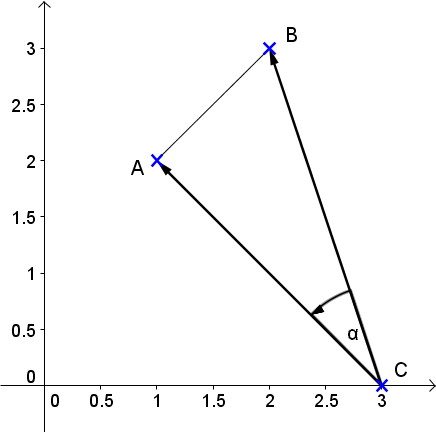
1. Lösungsweg: Flächenberechnung mit Determinante
Bestimme die Reihenfolge der Vektoren in der Determinante gegen den Uhrzeigersinn ( ) oder setze um die Determinante einen Betrag.
Wichtig: nicht vergessen!
Berechne die Determinante und erhalte dann das Ergebnis. Flächeneinheit dabei nicht vergessen, wenn gefordert.
2. Lösungsweg: Flächenberechnung mit Kreuzprodukt
Bette die Zeichenebene in den ein. Dies geschieht, indem jedem Vektor als dritte Komponente der Eintrag hinzugefügt wird.
Berechne nun das Kreuzprodukt . Das Ergebnis ist ein zu und orthogonaler Vektor, dessen Betrag dem Flächeninhalt des von und aufgespannten Parallelogramms entspricht. Die Hälfte davon entspricht dem gesuchten Flächeninhalt des Dreiecks ABC.
Hast du eine Frage oder Feedback?
Bilde die Vektoren und wende das Determinanten-Verfahren an.
- FE
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreiecksfläche berechnen
Zeichne die Punkte und das Dreieck in ein Koordinatensystem ein, um einen Überblick zu erhalten. Wähle eine Ecke, von der die Vektoren das Dreieck aufspannen, und berechne diese Vektoren.
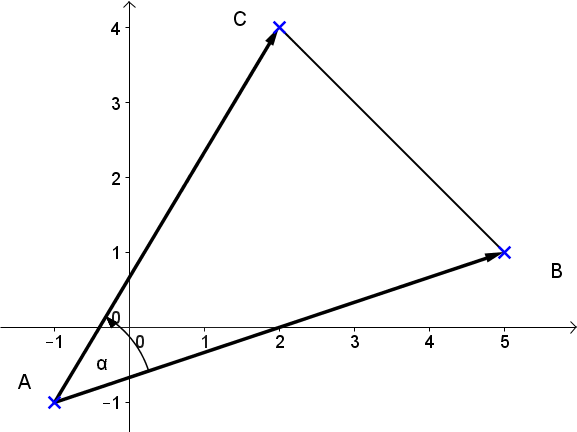
1. Lösungsweg: Flächenberechnung mit Determinante
Bestimme die Reihenfolge der Vektoren in der Determinante gegen den Uhrzeigersinn ( ) oder setze um die Determinante einen Betrag.
Wichtig: nicht vergessen!
Berechne die Determinante und erhalte dann das Ergebnis. Flächeneinheit dabei nicht vergessen, wenn gefordert.
2. Lösungsweg: Flächenberechnung mit Kreuzprodukt
Bette die Zeichenebene in den ein. Dies geschieht, indem jedem Vektor als dritte Komponente der Eintrag hinzugefügt wird.
Berechne nun das Kreuzprodukt . Das Ergebnis ist ein zu und orthogonaler Vektor, dessen Betrag dem Flächeninhalt des von und aufgespannten Parallelogramms entspricht. Die Hälfte davon entspricht dem gesuchten Flächeninhalt des Dreiecks ABC.
Hast du eine Frage oder Feedback?
Bilde die Vektoren und wende das Determinanten-Verfahren an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
