Aufgaben zur Flächenberechnung von Dreiecken im Koordinatensystem
Lerne mit diesen Aufgaben, Flächen von Dreiecken im Koordinatensystem zu berechnen.
- 1
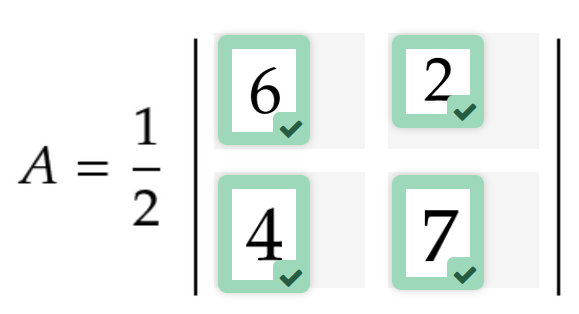
Flächeninhalt mit Determinante
Ziehe die Zahlen an die richtige Stelle in der Formel.
Berechne den Flächeninhalt des Dreiecks aus der Teilaufgabe (a).
- 2
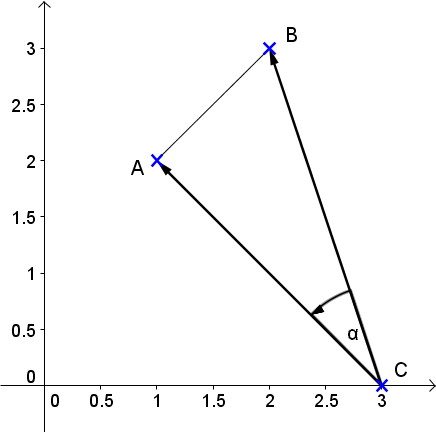
Berechne die Fläche der Dreiecke .
- FE
- FE
- 3
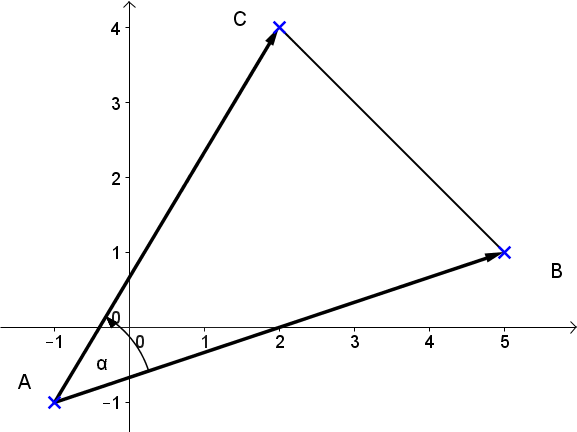
Die Punkte , und bilden ein Dreieck. Bestimme den Flächeninhalt mit dem Determinantenverfahren. Benutze als Fußpunkt.
FE
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?