Die gibt an, wie groß die in einer bestimmten ist.
Streckenabschnitte und Zeitspannen werden in der Physik mit der sog. Delta-Schreibweise, dem griechischen Buchstaben Δ angegeben.
Siehe auch: Delta-Schreibweise
Formel
Um die berechnen zu können, benötigst du die und die . Mit den folgenden Formeln kannst du diese berechnen:
:
➡ mit der Anfangsgeschwindigkeit und der Endgeschwindigkeit
:
➡ mit der Startzeit und Endzeit
Die wird mit folgender Formel berechnet:
Einheiten
Die Beschleunigung wird in der Physik in angegeben. Diese setzt sich aus den Einheiten der Geschwindigkeit und der Zeit wie folgt zusammen:
Beispielaufgabe
Ein Autofahrer fährt mit einer Geschwindigkeit von 50 und beschleunigt innerhalb von 6 auf 80 . Wie groß ist die Beschleunigung des Autos?
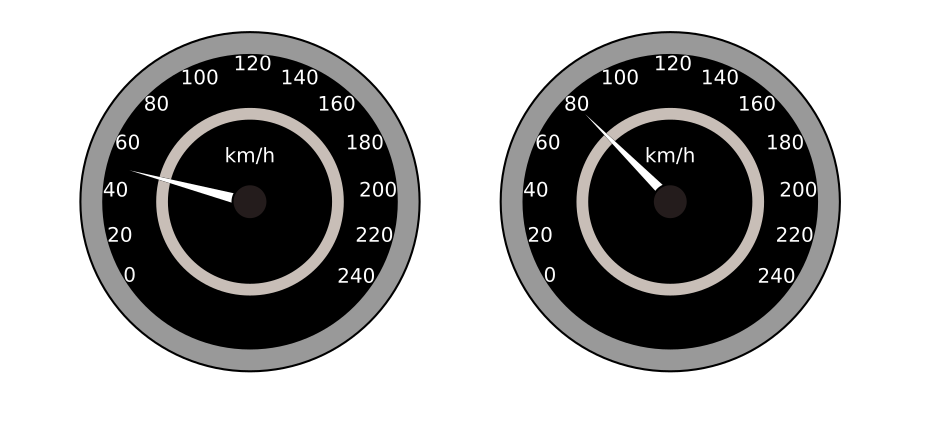
Lösung
Das Auto fährt zunächst mit einer Geschwindigkeit von 50 , sodass dies die Anfangsgeschwindigkeit ist. Das Fahrzeug beschleunigt auf eine Geschwindigkeit von 80 , welche somit die Endgeschwindigkeit des Autos darstellt.
Gegeben:
, und
Gesucht:
Lösung:
Die Geschwindigkeitsänderung ist in angegeben, die nun in umgerechnet werden kann. Die Umrechnung in ist nützlich für deine weitere Rechnung.
Das Ergebnis und die gegebene Zeitspanne können nun in die Formel für die Berechnung der Beschleunigung eingesetzt und vereinfacht werden.
Die Beschleunigung des Autos beträgt somit ca. .
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema: