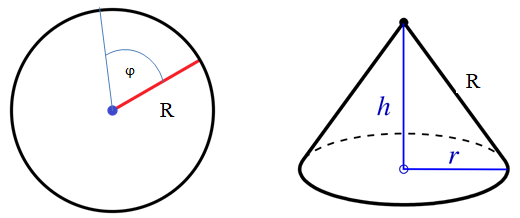
Aus einem kreisrunden Papierstück mit dem Radius R soll eine kegelförmige Popkorntüte hergestellt werden.
Wie muss das Papier zugeschnitten und zusammengeklebt werden, wenn die fertige Tüte mit möglichst viel Popcorn gefüllt werden soll?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Aus dem Kreis mit dem Radius wird ein Kreissektor mit dem Mittelpunktswinkel ausgeschnitten. Der ausgeschnittene Kreissektor ergibt den Mantel des Kegels.
Aufstellen der Zielfunktion und der Nebenbedingung
Die Zielfunktion bei dieser Aufgabe ist das Volumen eines Kegels:
Die Nebenbedingung ergibt sich aus der obigen rechten Abbildung.
Im rechtwinkligen Dreieck gilt der Satz des Pythagoras:
Die Volumenfunktion hängt sowohl von als auch von ab, d.h. .
Um die Nebenbedingung in die Zielfunktion einzusetzen kann man sie nach einer der beiden Variablen oder auflösen. Man hat somit zwei Lösungsvarianten.
Die einfachere dieser beiden Lösungsvarianten ergibt sich, wenn das Volumen des Kegels nur von der Kegelhöhe abhängig ist, d.h. es muss bestimmt werden.
Lösungsvariante 1
Einsetzen in die Zielfunktion
Gleichung wird nach bzw. gleich nach aufgelöst: .
Dieses wird nun in die Zielfunktion eingesetzt um die Extremalfunktion als Funktion von zu erhalten:
.
Für den Definitionsbereich gilt: .
Bestimmung des Extremwertes
Leite die Extremalfunktion zweimal ab, um den Extremwert und die Art des Extremwertes bestimmen zu können.
Setze die erste Ableitung gleich Null:
Nach aufgelöst erhält man: .
Da ist, gilt: .
Setze Gleichung in die zweite Ableitung ein:
Da die zweite Ableitung kleiner Null ist, ist der Extremwert ein Maximum.
Bestimmung des Kegelgrundkreisradius
Setzt man in ein,
so erhält man:
Zieht man nun die Wurzel aus , so erhält man für den Radius des Grundkreises des Kegels:
Bestimmung des Mittelpunktwinkels
Für die Bogenlänge des ausgeschnittenen Kreissektors gilt:
Die Bogenlänge ist der Umfang des Kegelgrundkreises mit dem Radius .
nach aufgelöst:
.
Setzt man Gleichung in Gleichung ein,
erhält man
Anmerkung: Der Winkel ist von unabhängig.
Das maximale Volumen in Abhängigkeit von
Setzt man die Gleichungen und in Gleichung ein, so erhält man das maximale Volumen:
Beantwortung der Ausgangsfrage
Die Popkorntüte hat ein maximales Volumen, wenn aus dem Kreis mit Radius ein Kreissektor mit dem Mittelpunktswinkel ausgeschnitten wird.
Der Radius des Kegelgrundkreises beträgt .
Die Höhe des Kegels beträgt und sein maximales Volumen ist
.
Lösungsvariante 2
Einsetzen in die Zielfunktion
Löst man Gleichung nach auf, erhält man:
Setzt man Gleichung in Gleichung ein, erhält man das Volumen in Abhängigkeit von :
Für den Definitionsbereich gilt: .
Anmerkung: Für und ist das Volumen gleich Null.
Bestimmung des Extremwertes
Leite die Extremalfunktion zweimal ab, um den Extremwert und die Art des Extremwertes bestimmen zu können. Für diese Ableitung benötigst du die Produktregel, die Ableitung einer Wurzel und die Kettenregel. Der Rechenaufwand für diese Ableitung ist relativ hoch. Mit einem Rechentrick kann man den Rechenaufwand verringern. Der Funktionsterm wird so umgeformt, dass der Term unter die Wurzel gezogen wird. Man erhält Gleichung .
Für die Ableitung von Gleichung genügt die Betrachtung des Radikanden.
Nimmt der Radikand einen maximalen Wert an, so ist auch die Wurzel aus diesem maximalen Radikanden ebenfalls maximal. Damit ist auch maximal.
Wir betrachten nun den Radikanden als Funktion von .
und suchen das Maximum dieser Funktion.
Setze die erste Ableitung gleich Null:
Die Gleichung hat die Lösungen (entfällt hier, da ) und die Lösung
Da ist, gilt .
Zur Überprüfung, ob es sich um ein Maximum handelt, setze Gleichung in die zweite Ableitung ein:
Da die zweite Ableitung kleiner Null ist, ist der Extremwert ein Maximum.
Bestimmung der Höhe des Kegels
In Gleichung wird die Gleichung eingesetzt:
Bestimmung des Mittelpunktswinkels
In Gleichung wird die Gleichung eingesetzt .
Anmerkung: der Winkel ist von unabhängig.
Das maximale Volumen in Abhängigkeit von
Setzt man die Gleichung in Gleichung ein, so erhält man das maximale Volumen in Abhängigkeit von : .
Beantwortung der Ausgangsfrage
Die Popkorntüte hat ein maximales Volumen, wenn aus dem Kreis mit Radius ein Kreissektor mit dem Mittelpunktswinkel ausgeschnitten wird.
Der Radius des Kegelgrundkreises ist .
Die Höhe des Kegels beträgt und sein maximales Volumen ist
.
Beispiel
Für einen Kreisradius von ergibt sich ein Kegelgrundkreisradius von
, eine Kegelhöhe von und ein Mittelpunktswinkel
von .
Das maximale Volumen in diesem Beispiel beträgt
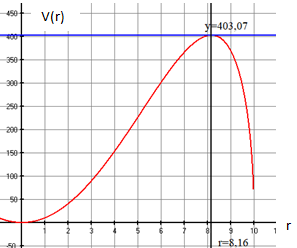
In der Abbildung ist die Extremalfunktion
für dargestellt.
Das Extremum befindet sich im Punkt
.
Mit den Maßen und
wurde ein Kegel hergestellt.
Unter dem Kegel befindet sich ein Lineal
zur Bestimmung des Durchmessers.

In diesem Bild ist die rechte Seite des Lineals zu sehen.
Es zeigt einen Durchmesser von
an. Der Radius beträgt
in guter Übereinstimmung mit dem berechneten Wert.

Bestimme die Zielfunktion und die Nebenbedingung. Ermittle daraus die Extremalfunktion und bestimme mit Hilfe der Ableitung den Extremwert.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch → Was bedeutet das?
