Analysis, Teil B, Aufgabengruppe 1

Betrachtet wird die Schar der in $R$ definierten Funktionen

g_{k} : x \mapsto k x^{3} + 3 \cdot (k + 1) x^{2} + 9 x mit k \in R ∖ {0}

und den zugehörigen Graphen $G_{k}$ . Für jedes $k$ besitzt der Graph $G_{k}$ genau einen Wendepunkt $W_{k}$ .

(2 BE)

Geben Sie das Verhalten von $g_{k}$ an den Grenzen des Definitionsbereichs in Abhängigkeit von $k$ an.

(3 BE)

Bestimmen Sie die x-Koordinate von $W_{k}$ in Abhängigkeit von $k$ .

(zur Kontrolle: $x = - \frac{1}{k} - 1)$

(4 BE)

Bestimmen Sie den Wert von $k$ so, dass der zugehörige Wendepunkt $W_{k}$ auf der y-Achse liegt. Zeigen Sie, dass in diesem Fall der Punkt $W_{k}$ im Koordinatenursprung liegt und die Wendetangente, d.h. die Tangente an $G_{k}$ im Punkt $W_{k}$ , die Steigung $9$ hat.

(2 BE)

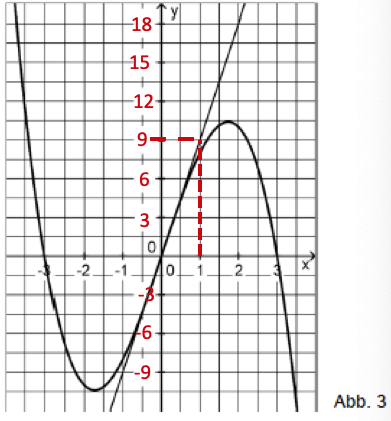
Für den in Aufgabe 3c bestimmten Wert von $k$ zeigt Abbildung 3 den zugehörigen Graphen mit seiner Wendetangente. In diesem Koordinatensystem sind die beiden Achsen unterschiedlich skaliert.

Bestimmen Sie die fehlenden Zahlenwerte an den Markierungsstrichen der y-Achse mithilfe eines geeigneten Steigungsdreiecks an der Wendetangente und tragen Sie die Zahlenwerte in Abbildung 3 ein.

In der Teilaufgabe ist eine Funktionenschar ganzrationaler Funktionen 3. Grades zu untersuchen.

Für jedes $k$ besitzt der Graph $G_{k}$ genau einen Wendepunkt $W_{k}$ .

Betrachtet wird die Schar der in $R$ definierten Funktionen

g_{k} : x \mapsto k x^{3} + 3 \cdot (k + 1) x^{2} + 9 x mit k \in R ∖ {0}

und dem zugehörigen Graphen $G_{k}$ .

Für jedes $k$ besitzt der Graph $G_{k}$ genau einen Wendepunkt $W_{k}$ .

Lösung Teilaufgabe a)

Da für jede Funktion $g_{k}$ der Definitionsbereich $R =] - \infty; + \infty [$ ist, bedeutet die Untersuchung des Verhaltens "an den Grenzen" des Definitionsbereichs die Bestimmung folgender Grenzwerte:

\lim_{x \to + \infty} g_{k} (x) und \lim_{x \to - \infty} g_{k} (x)

Da der Scharparameter $k$ sowohl negativ als auch positiv sein kann, ist zu erwarten, dass die Ergebnisse der Grenzwertbestimmungen vom zuständigen $k$ abhängen können.

So bestimmst du die Grenzwerte:

$\begin{array}{rcll} \lim_{x \to \pm \infty} g_{k} (x) & = & \lim_{x \to \pm \infty} [k x^{3} + 3 (k + 1) x^{2} + 9 x] & | x^{3} ausklammern \\ = & \lim_{x \to \pm \infty} x^{3} [k + \underset{\to 0}{\underset{⏟}{\frac{3 (k + 1)}{x}}} + \underset{\to 0}{\underset{⏟}{\frac{9}{x^{2}}}}] \\ = & \lim_{x \to \pm \infty} k \cdot x^{3} Jetzt Vorzeichen beachten: \\ \lim_{x \to + \infty} g_{k} (x) & = & + \infty falls k > 0 \\ = & - \infty falls k < 0 \\ \lim_{x \to - \infty} g_{k} (x) & = & - \infty falls k > 0 \\ = & + \infty falls k < 0 \end{array}$

Ergebnis

Für die ungeraden ganzrationalen Funktion 3. Grades $g_{k}$ gehen an den Grenzen des Definitionsbereichs, also für $x \to + \infty$ und für $x \to - \infty$ , die Funktionswerte entgegengesetzt gegen Unendlich. Der "Leitkoeffizient" $k$ bestimmt dies mit seinem Vorzeichen genauer.

Lösung Teilaufgabe b)

Die Wendepunkte ganzrationaler Funktionen 3. Grades sind zu bestimmen.

Notwendige Bedingung für das Vorliegen eines Wendepunktes ist, dass die 2. Ableitung an der Stelle Null wird.

So berechnest du die 1. und 2. Ableitung von $g_{k}$ :

$\begin{array}{rcll} g_{k} (x) & = & k x^{3} + 3 (k + 1) x^{2} + 9 x \\ g_{k}^{'} (x) & = & 3 k x^{2} + 6 (k + 1) x + 9 \\ g_{k}^{''} (x) & = & 6 k x + 6 (k + 1) \end{array}$

Setze $g_{k}^{''} (x)$ gleich Null und löse die Gleichung nach $x$ auf:

$\begin{array}{rcll} 6 k x + 6 (k + 1) & = & 0 & | - 6 (k + 1) \\ 6 k x & = & - 6 (k + 1) & | : 6 k \\ x & = & - \frac{1}{k} - 1 \end{array}$

Dass sich für diesen von $k$ abhängigen x-Wert $- \frac{1}{k} - 1$ tatsächlich ein Wendepunkt $W_{k}$ ergibt, bestätigt die 3. Ableitung $g_{k}^{'''} (x)$ , da sie von Null verschieden ist:

$g_{k}^{'''} (x) = 6 k \neq 0$ , wegen $k \in R ∖ {0}$ .

(4 BE)

Der Wendepunkt $W_{k}$ liegt auf der y-Achse, wenn sein x-Wert Null ist.

Setze den x-Wert des Wendpunkts gleich Null und löse die Gleichung nach $k$ auf:

$\begin{array}{rcll} - \frac{1}{k} - 1 & = & 0 & | \cdot k \\ - 1 - k & = & 0 & | + k \\ k & = & - 1 \end{array}$

Die Funktionsgleichung für $k = - 1$ lautet

$g_{- 1} (x) = - x^{3} + 9 x$ .

$x = 0$ liefert die y-Koordinate des Wendepunkts $W_{- 1}$ :

$g_{- 1} (0) = - 0^{3} + 9 \cdot 0 = 0$ .

Also liegt der Wendepunkt $W_{- 1}$ im Koordinatenursprung.

Für die Steigung von $g_{- 1}$ im Punkt $(0 | 0)$ erhältst du:

$g_{- 1}^{'} (x) = - 3 x^{2} + 9 \Rightarrow g_{- 1}^{'} (0) = 9$

Die Wendetangente der Funktionenschar hat also für die Funktion mit $k = - 1$ die Steigung $9$ .

Lösung Teilaufgabe d)

Als Steigungsdreieck der eingezeichneten Tangente nimmst du das Dreieck mit Koordinatenursprung, dem Punkt $(1 | 0)$ und dem Tangentenpunkt für $x = 1$ .

Der y-Wert dieses Tangentenpunktes hat den Wert $9$ .

Damit kannst du die y-Achse wie gewünscht skalieren.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?