Jedes Elektron kann durch seine vier Quantenzahlen genau beschrieben werden. Durch die Information, die du durch diese Zahlen erhältst, kannst du genau sagen, in welchem Orbital sich ein bestimmtes Elektron aufhält.
Quantenzahlen
Hauptquantenzahl n:
Beschreibt die Größe des Orbitals
Entspricht der Schale im Bohr´schen Atommodell
Nebenquantenzahl l:
Beschreibt die Form des Orbitals
Entspricht den jeweiligen Orbitalen (s-Orbital =0, p-Orbital =1 usw.)
Orientierungsquantenzahl :
Beschreibt die räumliche Ausrichtung der Orbitale
Entspricht den einzelnen Varianten der Orbitale (, oder )
Spinquantenzahl :
Beschreibt die Energie des jeweiligen Elektrons
Hier gibt es nur zwei Möglichkeiten: den Alpha-Spin (+1/2) und den Beta-Spin (-1/2)
Diese ist besonders wichtig, will man das Pauli Prinzip anwenden. Die beiden Elektronen in einem Orbital stimmen sowohl in Haupt-, Neben- und Orientierungsquantenzahl überein. Um sich in mindestens einer Quantenzahl zu unterscheiden, brauchen sie unterschiedliche Spins.
Ein Beispiel zu den Quantenzahlen:
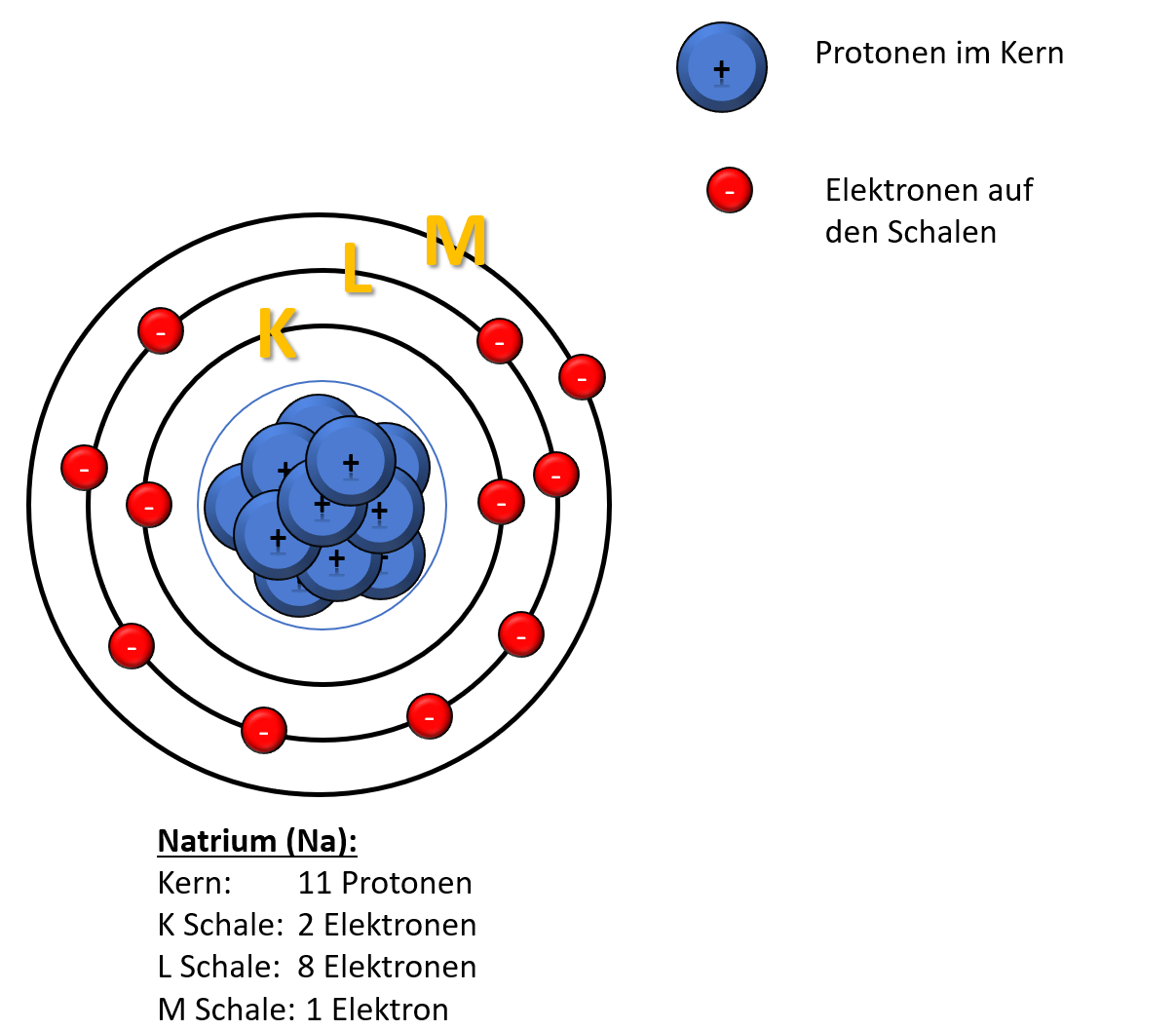
Wenn du dir das einzelne Elektron auf der M-Schale anschaust, dann weißt du bereits die Hauptquantenzahl. Denn diese entspricht der Schale im Schalenmodell. In diesem Fall hier ist das also n = 3.
Die Nebenquantenzahl lässt sich auch sehr leicht herausfinden. Da dein betrachtetes Elektron das Erste auf der Schale ist, muss es folglich zu einem s-Orbital gehören. Es ergibt sich also l = 0.
Da das s-Orbital nur eine mögliche Ausrichtung hat (nicht wie beispielsweise die p-Orbitale, die sich entlang der drei Achsen ausrichten können), steht auch unsere Orientierungsquantenzahl schon fest. Es muss hier also =0 eingesetzt werden.
Bei der Spinquantenzahl hast du nur zwei Möglichkeiten. Entweder den Alpha- oder den Beta-Spin. Da dein betrachtetes Elektron, das erste in dem s-Orbital ist, wird es den energetisch günstigeren Zustand des Alpha-Spins annehmen. Somit beträgt die Spinquantenzahl =+1/2.
Dein betrachtetes Elektron kann also folgendermaßen beschrieben werden:
n= 3, l=0, =0 und = +1/2
Wie du oben schon gelernt hast, kann nur dein Elektron diese Kombination an Quantenzahlen annehmen. Jedes andere Elektron in dem oben gezeigten Natrium Atom hat eine andere Kombination.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
