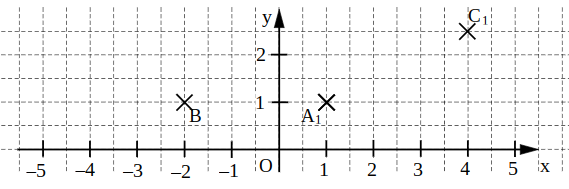
Das Rechteck wird durch Parallelverschiebung mit dem Vektor auf das Rechteck abgebildet. Ergänze in der Zeichnung die Rechtecke und
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Das Rechteck wird durch Parallelverschiebung mit dem Vektor auf das Rechteck abgebildet. Ergänze in der Zeichnung die Rechtecke und
