Ordne jedem der Funktionsgraphen die passende Funktion zu.
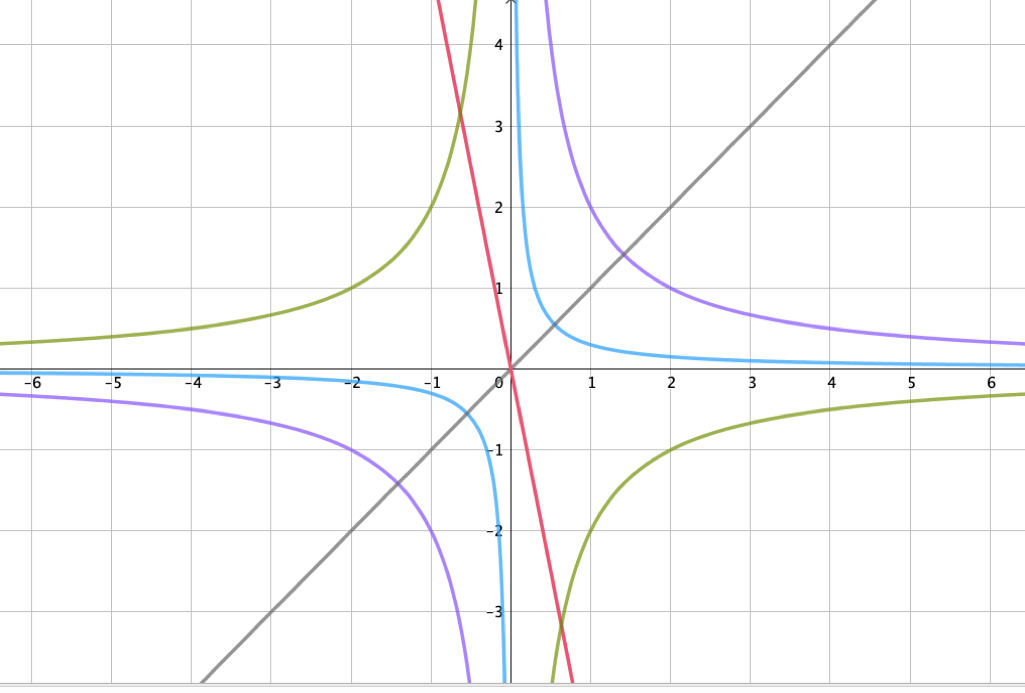
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
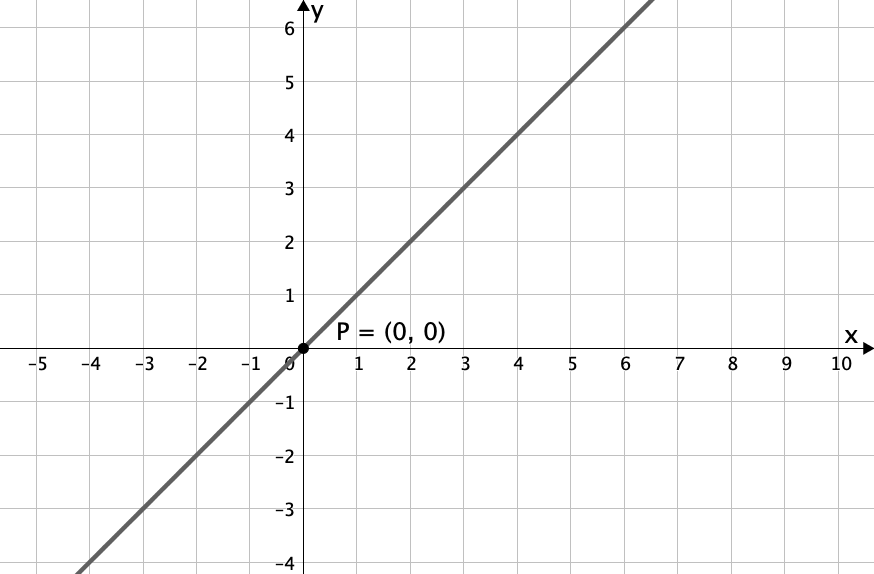
Bei der ersten Funktion handelt es sich um eine Funktion der Form , wobei in diesem Fall die Steigung und der y-Achsenabschnitt ist. Den Graphen einer Funktion solcher Form nennt man eine Gerade.
Mit diesen Informationen weißt du auch, dass es sich um eine steigende Gerade handelt und demnach kannst die Funktion dem Graphen zuordnen.
Überprüfen kannst du dies, indem du einen Punkt auf dem Graphen abliest und diesen in die Funktion einsetzt.
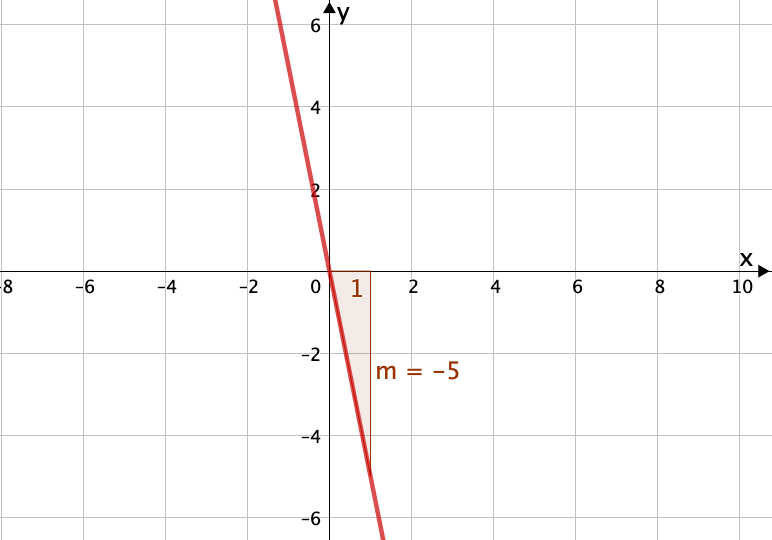
Ähnlich wie bei der vorherigen Funktion handelt es sich bei der letzten Funktion um eine lineare Funktion mit der Steigung und dem y-Achsenabschnitt .
Die Steigung dieser Funktion ist negativ und somit handelt es sich um eine fallende Gerade. Also kannst du die Funktion dem Graphen zuordnen.
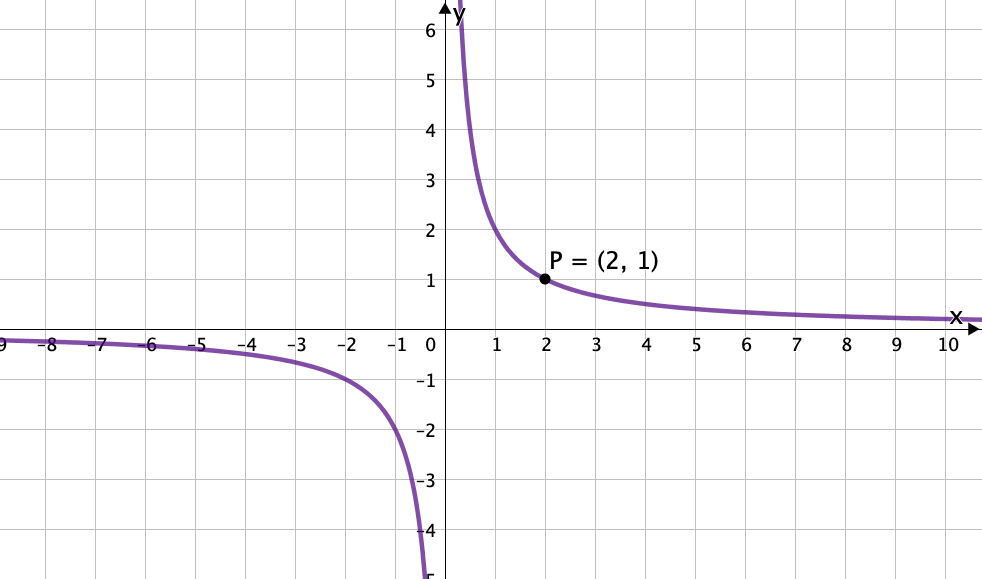
Aus der Form der Funktion kannst du entnehmen, dass es sich bei dem Graphen dieser Funktion um eine Hyperbel handelt mit der positiven Öffnung . Das heißt der Graph befindet sich im 1. und 3. Quadranten.
Also hast du von den 5 Graphen 2 (blau und lila), die in Frage kommen würden. Um herauszufinden welcher dieser Graphen die richtige ist, kannst du einen günstigen x-Wert in die Funktion einsetzten und schauen, welcher y-Wert rauskommt. Anschließend kannst du überprüfen auf welchem Graph sich der Punkt befindet.
Beispiel:
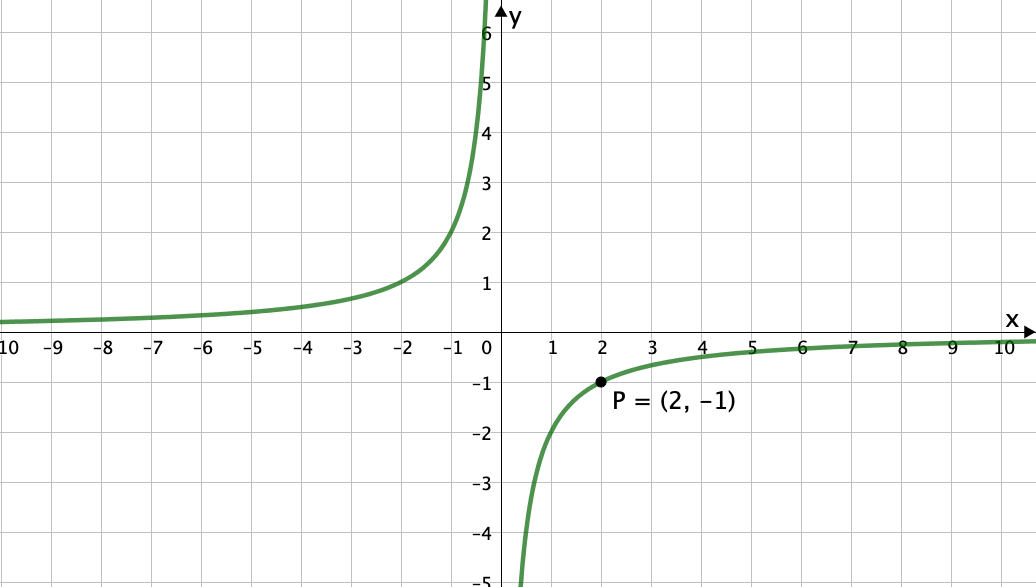
Auch hier handelt es sich um eine Hyperbel. Dieses Mal besitzt die Hyperbel eine negative Öffnung . Das heißt der Graph befindet sich im 2. und 4. Quadranten. Somit kommt für die Funktion nur der Graph in Frage.
Die Überlegung kannst du überprüfen, indem du einen günstigen und gut ablesbaren Punkten vom Graphen entnimmst und den in die Funktion einsetzt.
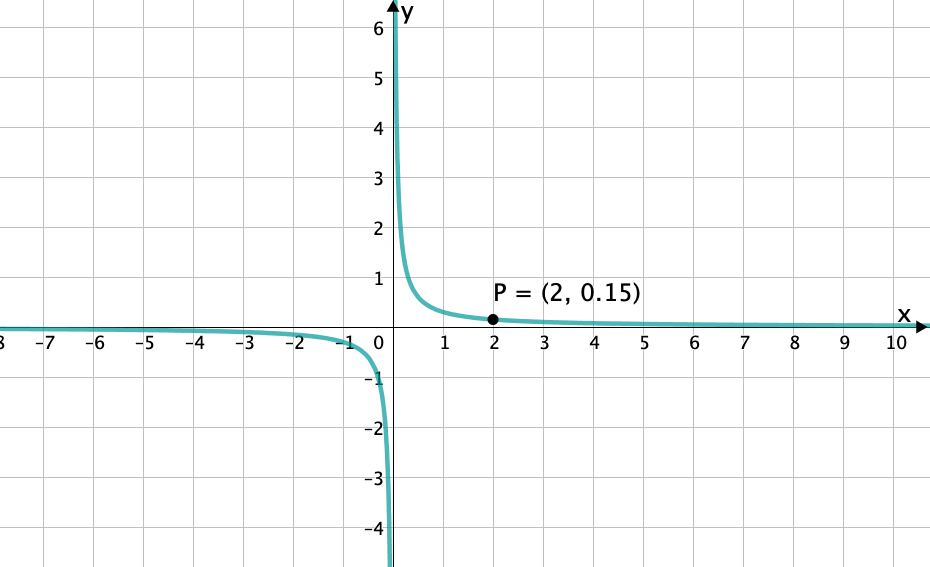
Bei der Funktion handelt es sich ebenfalls um eine Hyperbel mit der positiven Öffnung . Also befindet sich der Graph im 1. und 3. Quadranten. Somit ist es entweder der lila Graph oder der blaue Graph.Um herauszufinden welcher dieser Graphen die richtige ist, kannst du einen günstigen x-Wert in die Funktion einsetzten und schauen, welcher y-Wert rauskommt. Anschließend kannst du überprüfen auf welchem Graph sich der Punkt befindet.
Beispiel:
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
