Flächeninhalte und Volumen im kartesischen Koordinatensystem

Inhalte über Koordinatendifferenz bestimmen

Um den Flächeninhalt über die Koordinatendifferenz zu bestimmen, müssen die zur Berechnung der Fläche notwendigen Längen parallel zu den Koordinatenachsen sein. Nun werden die Längen der benötigten Seiten über Differenzen von Punktkoordinaten bestimmt und in die entsprechende Formel eingesetzt.

Beispiel

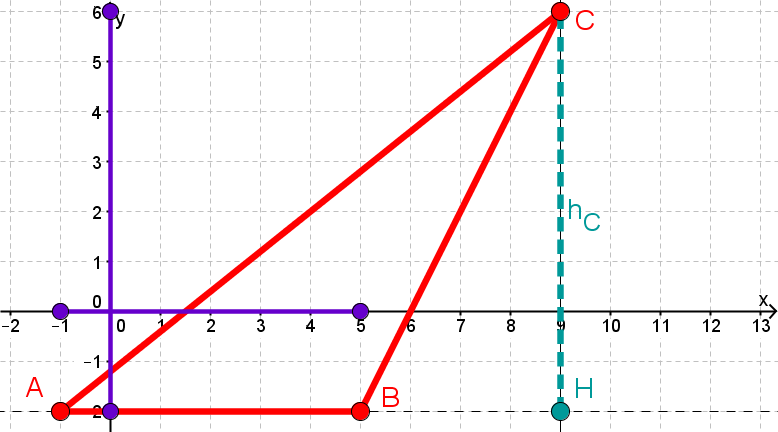
Nun müssen die Grundlinie g und die Höhe h bestimmt werden.

Bestimmung der Grundlinie

Die Grundlinie ist parallel zur x-Achse und wird durch die Punkte A und B bestimmt. 

Die Differenz der x-Koordinaten von A und B ist damit die Länge der Grundlinie.

$\mathrm g={\mathrm x}_\mathrm b-{\mathrm x}_\mathrm a=5-(-1)=5+1=6\;\mathrm{LE}\\$

Bestimmung der Höhe h

Die Höhe h ist parallel zur y-Achse und wird durch die Differenz der y-Koordinaten von $C$ und $A$ oder $B$ berechnet. Die y-Koordinate von $A$ und $B$ muss gleich sein, da sie sonst nicht parallel zur x-Achse wären.

$\mathrm h={\mathrm y}_\mathrm c-{\mathrm y}_\mathrm a=6-(-2)=6+2=8\;\mathrm{LE}$

Die Werte müssen nun noch in die Formel für den Flächeninhalt des Dreiecks eingesetzt werden.

$A=\frac12\cdot h\cdot g=\frac12\cdot8\;LE\cdot6\;LE=24\;FE$

Damit ist der Flächeninhalt $24\;\text{FE}$.

Weitere Hinweise:

Die Differenzen müssen immer positiv sein, da sonst ein nicht positiver Flächeninhalt berechnet wird.

• $\text{LE}$ steht für Längeneinheit, $\text{FE}$ steht für Flächeninhalt.

• Die Methode kann auch zur Bestimmung vom Volumina eines Körpers genutzt werden, dies wird jedoch nur sehr selten gemacht.

Inhalte über Vektoren    

Die Fläche oder das Volumen einer nicht achsenparallelen Figur wird über Vektoren bestimmt. Dazu gibt es bestimmte Formeln, die im Folgenden aufgeführt werden. Hilfreich ist auch die Eigenschaft des Kreuzproduktes im 3-Dimensionalen Koordinatensystem, da es halbiert die Fläche des von den Vektoren aufgespannten Dreiecks ergibt.

Flächeninhalt eines Dreiecks ABC  

Der Inhalt eines Dreiecks ABC:

Im Zweidimensionalen

$\mathrm A=\frac12\left|\left({\mathrm a}_1{\mathrm b}_2-{\mathrm a}_2{\mathrm b}_1\right)+\left({\mathrm b}_1{\mathrm c}_2-{\mathrm b}_2{\mathrm c}_1\right)+\left({\mathrm c}_1{\mathrm a}_2-{\mathrm c}_2{\mathrm a}_1\right)\right|$

Im Dreidimensionalen

$\mathrm A=\frac12\left|\overrightarrow{\mathrm{AB}}\times\overrightarrow{\mathrm{AC}}\right|\\$

Flächeninhalt eines Parallelogramms        

Inhalt eines Parallelogramms, welches von den Vektoren  $\overrightarrow{\mathrm a}$  und  $\overrightarrow{\mathrm b}$  im 2-Dimensionalen aufgespannt wird:

$\mathrm A=\left|{\mathrm a}_1{\mathrm b}_2-{\mathrm a}_2{\mathrm b}_1\right|$

Inhalt eines Parallelogramms, welches von den Vektoren  $\overrightarrow{\mathrm c}$  und  $\overrightarrow{\mathrm d}$  im 3-Dimensionalen aufgespannt wird:

$\mathrm A=\left|\overrightarrow{\mathrm c}\times\overrightarrow{\mathrm d}\right|$

Man muss jedoch beachten, dass man den durch das Kreuzprodukt entstehenden Vektor nicht vergrößern oder verkleinern darf. 

Volumen einer dreiseitigen Pyramide      

Die Volumenformel für eine dreiseitige Pyramide:

$\def\arraystretch{1.25} \begin{array}{l}\mathrm V=\frac16\left|\overrightarrow{\mathrm a}\circ\left(\overrightarrow{\mathrm b}\times\overrightarrow{\mathrm c}\right)\right|=\frac16\left|\det\left(\overrightarrow{\mathrm a},\overrightarrow{\mathrm b},\overrightarrow{\mathrm c}\right)\right|\end{array}$