Flächenberechnung in der analytischen Geometrie

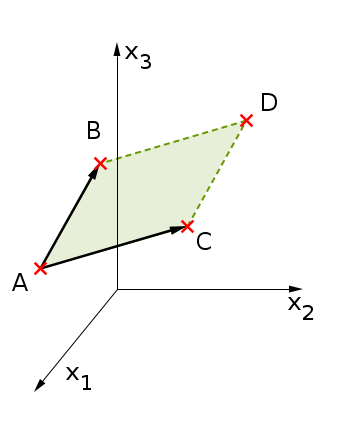
Mit Determinanten lassen sich Flächeninhalte von Dreiecken und Parallelogrammen gut ausrechnen.

Mit $\begin{vmatrix}{a}_{11}&{a}_{12}\\{a}_{21}&{a}_{22}\end{vmatrix}=\det\begin{pmatrix}{a}_{11}&{a}_{12}\\{a}_{21}&{a}_{22}\end{pmatrix}$ wird hier die Determinante bezeichnet.

Inhalt eines Dreiecks ABC

Im Zweidimensionalen

Fläche $A = \frac{1}{2}\left|\mathrm{det}\begin{pmatrix}\overrightarrow{{{AB}}}&\overrightarrow{{AC}}\end{pmatrix}\right|$

Herleitung:

Die Fläche des aufgespannten Dreiecks lässt sich als halbe Fläche eines Parallelogramms (unten) berechnen.

Seien dazu die Punkte $A, B$ und $C$ in der Ebene gegeben.

Seien $\overrightarrow{{AB}}=\begin{pmatrix}{x}_1\\{x}_2\end{pmatrix}$ und $\overrightarrow{AC}=\begin{pmatrix}{y}_1\\{y}_2\end{pmatrix}$ , dann

ist:

$\ {A}_{ABC}=\frac12\left|\det\begin{pmatrix}\overrightarrow{AB}&\overrightarrow{AC}\end{pmatrix}\right|=$

$=\frac12\left|\det\begin{pmatrix}{x}_1&{x}_2\\{y}_1&{y}_2\end{pmatrix}\right|=\frac12\left|x_1y_2-x_2y_1\right|$

Die Reihenfolge der Vektoren ist egal, solange der Ausdruck in Betragsstrichen steht.

Geogebra File: https://assets.serlo.org/legacy/7175_sJk8fsSkQY.xml

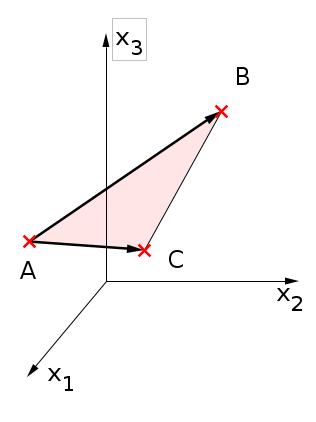
Im Dreidimensionalen

Fläche $A=\frac{1}{2}\left|\overrightarrow{AB}\times\overrightarrow{AC}\right|$

Die Fläche des aufgespannten Dreiecks lässt sich als halbe Fläche eines Parallelogramms (unten) berechnen.

$\overrightarrow{AB}=\begin{pmatrix}{x}_1\\{x}_2\\{x}_3\end{pmatrix}, \quad \overrightarrow{AC}=\begin{pmatrix}{y}_1\\{y}_2\\{y}_3\end{pmatrix}$

${A}_{ABC}=\frac{1}{2}\left|\overrightarrow{AB}\times\overrightarrow{AC}\right|=\frac12\left|\begin{pmatrix}x_2y_3-x_3y_2\\x_3y_1-x_1y_3\\x_1y_2-x_2y_1\end{pmatrix}\right|=\frac12\sqrt{\left(x_2y_3-x_3y_2\right)^2+\left(x_3y_1-x_1y_3\right)^2+\left(x_1y_2-x_2y_1\right)^2}$

Geogebra File: https://assets.serlo.org/legacy/7291_Fauk6FBOR3.xml

Inhalt eines Parallelogramms

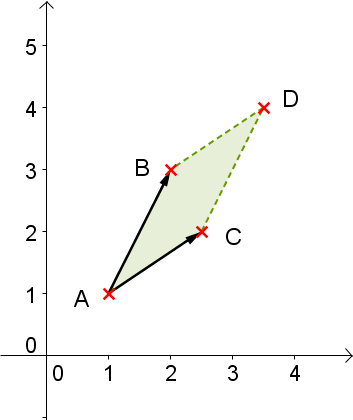
Im Zweidimensionalen

Inhalt eines Parallelogramms, welches von den Punkten $A,B,C$ und deren Verbindungsvektoren $\overrightarrow{{AB}}, \overrightarrow{{AC}}$ .

Fläche $A =\left|\det\begin{pmatrix}\overrightarrow{{AB}}&\overrightarrow{AC}\end{pmatrix}\right|$

Herleitung:

Die Fläche des aufgespannten Parallelogramms lässt sich mit dem Betrag der Determinante der aufspannenden Vektoren berechnen.

Seien dazu die Punkte $A$ , $B$ und $C$ in der Ebene gegeben.

Seien $\overrightarrow{{AB}}=\begin{pmatrix}{x}_1\\{x}_2\end{pmatrix}$ und $\overrightarrow{AC}=\begin{pmatrix}{y}_1\\{y}_2\end{pmatrix}$ , dann ist ${A}_{ABC}=\left|\det \begin{pmatrix}\overrightarrow{AB}&\overrightarrow{AC}\end{pmatrix}\right|=\left|\det\begin{pmatrix}{x}_1&{x}_2\\{y}_1&{y}_2\end{pmatrix}\right|=\left|x_1y_2-x_2y_1\right|$

Die Reihenfolge der Vektoren ist egal, solange der Ausdruck in Betragsstrichen steht.

Geogebra File: https://assets.serlo.org/legacy/5553_Lw8wToEYIX.xml

Im Dreidimensionalen

Inhalt eines Parallelogramms, welches von den Punkten $A, B, C$ und ihren Verbindungsvektoren $\overrightarrow{AB}$ und $\overrightarrow{AC}$ im 3-Dimensionalen aufgespannt wird.

Fläche $A=\left|\overrightarrow{AB}\times\overrightarrow{AC}\right|$

Herleitung:

Die Fläche des aufgespannten Parallelogramms lässt sich mit dem Betrag des Vektorprodukts der aufspannenden Vektoren berechnen.

$\overrightarrow{AB}=\begin{pmatrix}{x}_1\\{x}_2\\{x}_3\end{pmatrix}, \quad \overrightarrow{AC}=\begin{pmatrix}{y}_1\\{y}_2\\{y}_3\end{pmatrix}$

${A}_{ABC}=\left|\overrightarrow{AB}\times\overrightarrow{AC}\right|=\left|\begin{pmatrix}x_2y_3-x_3y_2\\x_3y_1-x_1y_3\\x_1y_2-x_2y_1\end{pmatrix}\right|=\sqrt{\left(x_2y_3-x_3y_2\right)^2+\left(x_3y_1-x_1y_3\right)^2+\left(x_1y_2-x_2y_1\right)^2}$

Geogebra File: https://assets.serlo.org/legacy/7293_oBCs9F4kRc.xml

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?