Kreiszahl Pi

Die Kreiszahl $\mathrm\pi$ ist eine der wichtigsten Konstanten in der Mathematik.

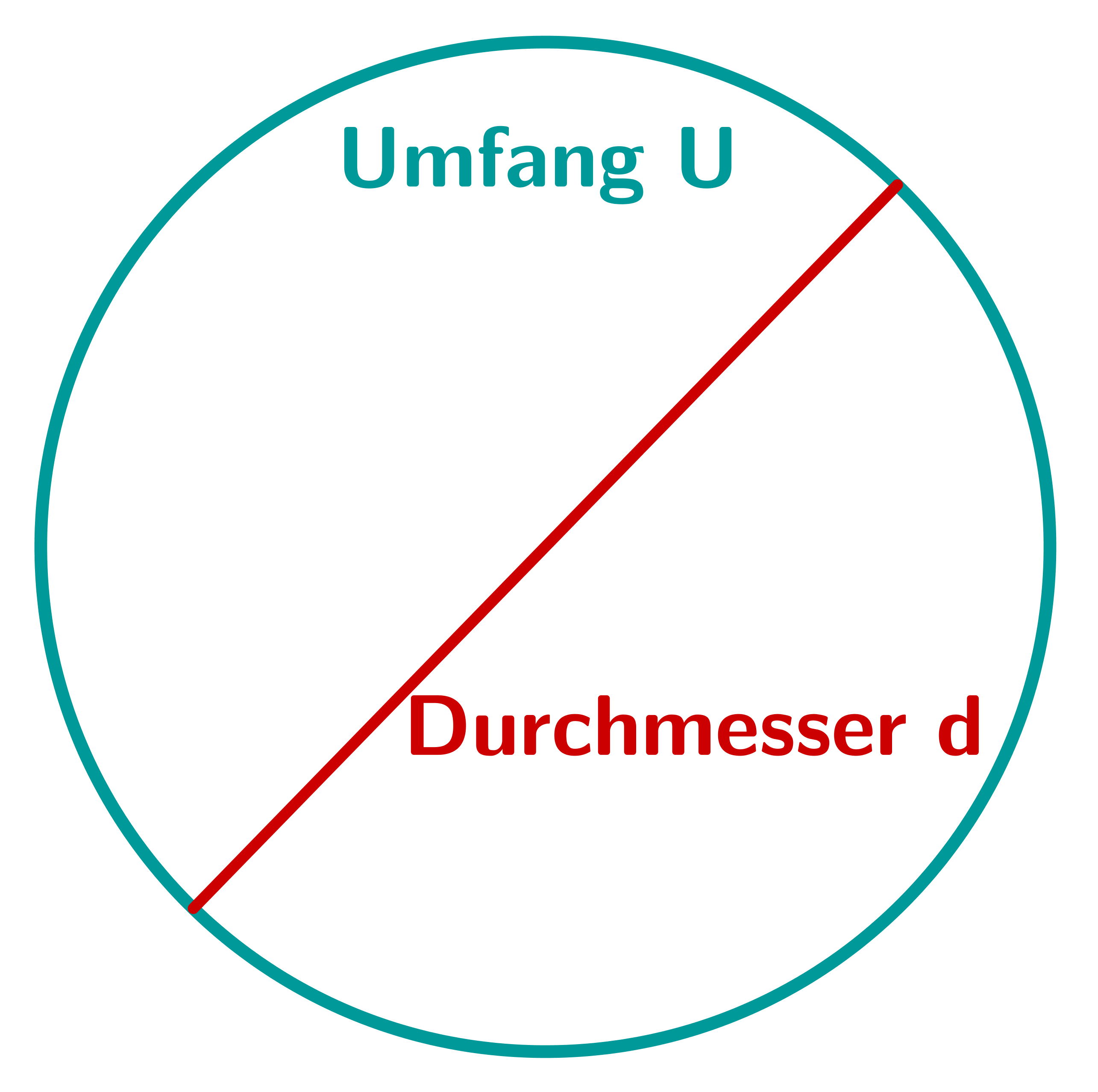
Näherungsweise ist $\mathrm\pi\approx3{,}14159$ . $\pi$ ist das Verhältnis zwischen dem Umfang eines Kreises und dessen Durchmesser.

Es gilt $\pi = \dfrac{\color{#009999}U}{\color{#cc0000}d}$ .

Übungen zum Verständnis

Konstruiere die Kreise mit Radius $r=2\;\text{cm}$ , $r = 3\;\text{cm}$ , $r = 4\;\text{cm}$ und $r = 5\;\text{cm}$ und miss jeweils den Kreisumfang. Erstelle eine Wertetabelle mit jeweiligem Durchmesser und Umfang. Trage die Wertepaare in ein Koordinatensystem ein, die Durchmesser auf der x-Achse, die Umfänge auf der y-Achse.

Welcher Graph ergibt sich? (abgesehen von Messungenauigkeiten)

Wie passt dieser Graph zur Beziehung $\pi = \dfrac{\color{#009999}U}{\color{#cc0000}d}$ ?

Miss Durchmesser und Umfang weiterer Kreisformen aus dem Alltag, z. B. Klebebandrollen, Teller, usw. und berechne ihr Verhältnis.

Formeln mit $\pi$

Flächeninhalt eines Kreises	$A=\pi r^2$
Umfang eines Kreises	$U=2\pi r$

Die Irrationalität von $\pi$

$\pi$ ist irrational. Das heißt, man kann $\pi$ nicht als Bruch $\frac{a}{b}$ aus ganzen Zahlen $a$ und $b$ schreiben.

Das bedeutet, dass $\pi$ unendlich viele Nachkommastellen hat, die sich nicht periodisch wiederholen.

Rechts sieht man die ersten Nachkommastellen von $\pi$ .

3,141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091 ...

Bestimmung von $\pi$

Es gibt viele verschiedene Möglichkeiten $\pi$ anzunähern (= immer genauer zu berechnen). Eine Möglichkeit ist die Monte-Carlo-Methode.

Man zeichnet zuerst einen Kreis mit Radius $r$ in ein Quadrat mit Seitenlänge $2r$ ein.
Dann lässt man den Computer zufällig Punkte in dem Quadrat erzeugen. (Man kann sich das vorstellen, als würde man aus einer ausreichenden Höhe einen Stift immer wieder auf ein Blatt Papier fallen lassen, auf dem ein Quadrat und ein Kreis gemalt sind.)
Man zählt dann, wie viele Punkte auf den Kreis und wie viele auf das gesamte Quadrat fallen.

Kreiszahl Pi Monte Carlo — Der Computer hat hier $999$ Punkte erzeugt.

Hat der Kreis den Radius $r$ , gilt für den Flächeninhalt vom Kreis $A_{\text{Kreis}}=\pi r^2$ und vom Quadrat $A_{\text{Quadrat}}=(2r)^2=4r^2$ .

Das Verhältnis der zufälligen Punkte im Kreis zu den Punkten im Quadrat entspricht ungefähr dem Verhältnis der Flächen:

$\dfrac{A_{\text{Kreis}}}{A_{\text{Quadrat}}} \approx \dfrac{\text{Punkte im Kreis}}{\text{Punkte im Quadrat}} = \dfrac{811}{999}$

$\dfrac{\pi r^2}{4r^2}=\dfrac{\pi}{4} \approx \dfrac{811}{999}$

$\pi \approx \dfrac{811}{999} \cdot 4 \approx 3{,}247$

Das Ergebnis weicht weniger als $4\;\%$ von $\pi$ ab. Möchte man ein genaueres Ergebnis, braucht man noch mehr zufällige Punkte.

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?