Die Periode einer Dezimalzahl mit unendlichen Nachkommastellen ist eine Folge von Ziffern, die sich unendlich oft wiederholt.
Als Zeichen für die Periode verwendet man einen waagrechten Strich über den Ziffern, die sich wiederholen.
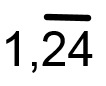
Beispiel | Sprechweise |
|---|---|
Der Bruch hat die Periode 3. | Man liest die Dezimalzahl als: Null Komma Periode 3. |
Der Bruch hat die Periode 16. | Man liest sie als: Null Komma Periode 16. |
Der Bruch hat die Periode 6 (nicht 16) | Man liest sie als: Null Komma 1 Periode 6. |
Der Bruch hat die Periode 285714. | Man liest sie als: Null Komma Periode 285714 |
Der Bruch hat keine Periode. | Man liest sie als: Null Komma sieben fünf |
Reinperiodische Dezimalzahlen
Als reinperiodische Dezimalzahlen bezeichnet man Zahlen, bei denen die Periode direkt hinter dem Komma beginnt.
Gemischtperiodische Dezimalzahlen
Als gemischtperiodische Dezimalzahlen bezeichnet man periodische Zahlen, bei denen zwischen dem Komma und der Periode noch eine oder mehrere Zahlen stehen, d.h. die Periode beginnt nicht direkt hinter dem Komma.
Umwandlung einer periodischen Dezimalzahl in einen Bruch
Eine periodische Dezimalzahl lässt sich auch immer als Bruch schreiben. Wie man von der Dezimalzahlschreibweise auf die Bruchschreibweise kommt, kann man im Artikel Umrechnen von Dezimalzahlen in Brüche nachlesen.
Satz über die Länge einer Periode
Jede Dezimalzahl kann höchstens eine so lange Periode haben wie der Nenner im entsprechenden Bruch minus .
Der Bruch hat höchstens eine Periode der Länge , da ist.
hat eine Periodenlänge von .
Der Bruch hat höchstens eine Periode der Länge , da ist.
hat eine Periodenlänge von .
Der Bruch hat höchstens eine Periode von , da ist.
hat nur eine Periodenlänge von .
Am letzten Beispiel sieht man deutlich, dass der Satz nur eine Aussage über die maximale Periodenlänge macht (und nicht über die exakte Periodenlänge).
Der Satz gilt übrigens in sämtlichen Stellenwertsystemen. wäre z.B. unser im Heptadezimalsystem.
Eindeutigkeit der Dezimaldarstellung
Man ist aus der Mathematik gewohnt, dass diese eine exakte und damit eindeutige Wissenschaft ist. Bei der Dezimalbruchschreibweise tritt nun eine Uneindeutigkeit auf. Es gilt nämlich:
Man kann die 1 durch zwei unterschiedlichen Dezimalzahlen darstellen: Durch die bekannte 1 und durch .
Viele anderen Zahlen haben natürlich auch mehrdeutige Darstellungsmöglichkeiten als Dezimalzahl:
usw.
Unendlich viele, nichtperiodische Nachkommastellen
Es gibt auch Dezimalzahlen, die unendlich viele Nachkommastellen haben, die sich aber nicht periodisch wiederholen. Solche Zahlen nennt man irrationale Zahlen. Diese sind in den reellen Zahlen enthalten.
Die irrationalen Zahlen kann man nicht als Bruch darstellen!
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
