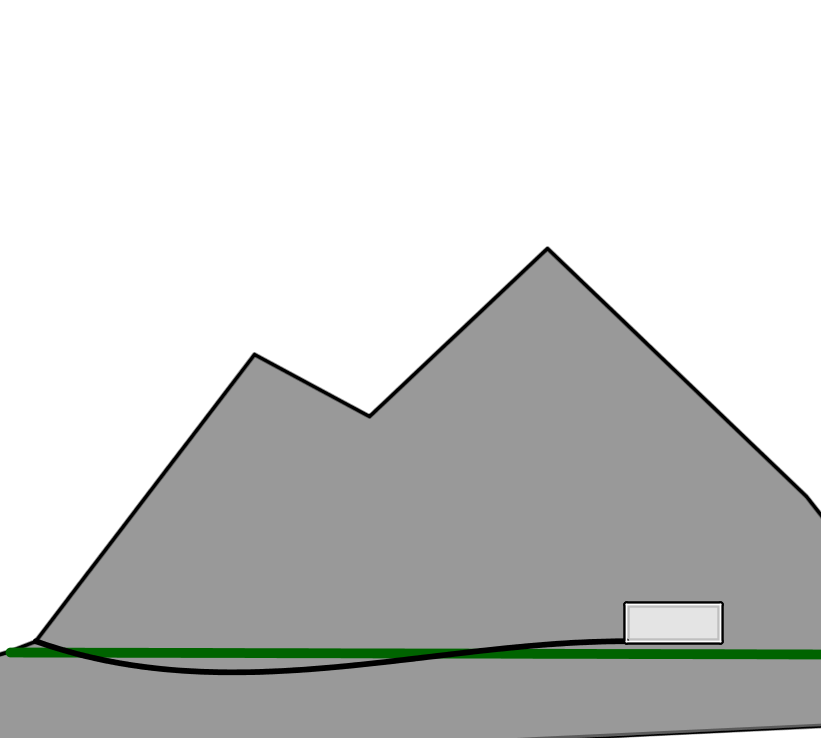
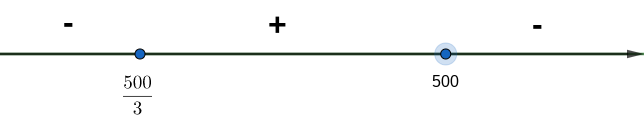Eine Gemeinde möchte in einem Gebirgsmassiv, in dem sich eine waagrecht verlaufende, geologisch interessante Schicht befindet, ein kleines Museum errichten, welches Besuchern einen Einblick in die Besonderheiten der Gesteinsformation geben soll.
Geplant ist ein Ausstellungsraum mit Erklärungstafeln, Tonbildschau und ähnlichem, der sich ca. 500 m weit innerhalb des Berges befinden soll, und zu dem die Besucher mit einer kleinen Bahn hingebracht werden.
Die Bahnstrecke soll dabei so geführt werden, dass die Besucher während der Fahrt einen möglichst guten Einblick in die interessante Gesteinsschicht bekommen.
Skizze nicht maßstabsgetreu
Nach dem Architektenentwurf liegt der Punkt, in dem der Zug in den Berg hineinfahren soll, 1,55 m oberhalb der Höhe der Gesteinsschicht. Von dort aus verläuft die geplante Strecke in einer leicht geschwungenen Linie teils oberhalb, teils unterhalb der Schicht bis zu dem Ausstellungsraum.
Wählt man den oberen Rand der Gesteinsschicht als -Achse, und setzt am Einstiegspunkt der Bahn in den Berg , so wird der Höhenverlauf der Strecke für angenähert beschrieben durch die Funktion mit
wobei und in Metern gemessen werden.
Berechne den Neigungswinkel gegen die Horizontale, in dem der Zug im Punkt in den Berg einfährt.
Bestimme rechnerisch die Stelle , an der die Bahnstrecke ihren tiefsten Punkt erreicht. Runde dabei auf zwei Stellen hinter dem Komma. Wie tief unterhalb des unteren Randes der Gesteinsschicht liegt dieser Punkt, wenn die Gesteinsschicht ca. 80 cm dick ist? (Teilergebnis: )
Im Endpunkt fährt der Zug in den Ausstellungsraum ein. Begründe durch eine geeignete Rechnung, dass der Übergang von der geschwungenen Bahnstrecke auf den waagrecht liegenden Ausstellungsraum ohne Knick erfolgt.
Welche mittlere Steigung überwindet die Lokomotive zwischen dem tiefsten Punkt der Strecke und dem Endpunkt ? An welchen Stellen ist die lokale Steigung gerade genauso groß wie diese mittlere Steigung?
Welche Steigung muss die Lokomotive zwischen dem tiefsten Punkt und maximal bewältigen?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?