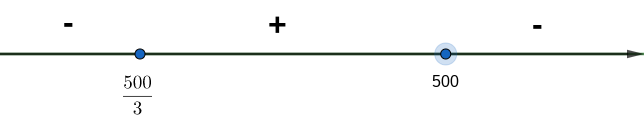Anwendungsaufgaben der Differential- und Integralrechnung
Wie hängen Steigung und Fläche zusammen? Vertiefe dein Wissen über die Differential- und Integralrechnung mit diesen Übungsaufgaben!
- 1
Eine Schaustellerfamilie ist seit Jahrzehnten mit ihrer Achterbahn auf Volksfesten vertreten. Nun bestellt sie bei einem Hersteller ein neues Modell.
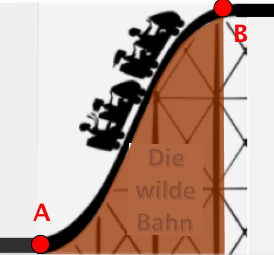
Sie erhält für den Aufstiegsteil der Bahn das abgebildete (nicht maßstabsgetreue) Angebot.
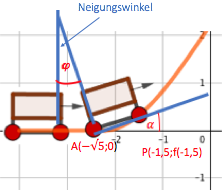
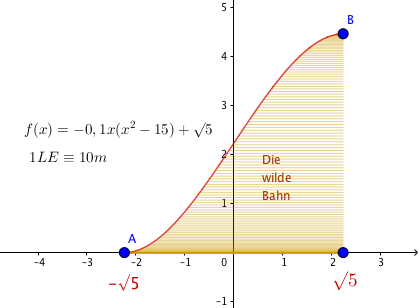
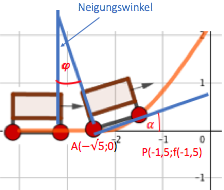
Der zahnradbetriebene Aufstiegsteil dem die Mittelpunkte der Wagenräder folgen, beginnt demnach nach einer kurzen horizontalen Fahrt ohne Knick im Punkt und verläuft von da an nach der Funktion
bis zum höchsten Achterbahnpunkt , ab dem sich (wieder ohne Knick) eine kurze horizontale Strecke bis zur ersten Abfahrt anschließt.
Im Familienkreis wird über das Angebot beraten.
Der Seniorchef legt Wert darauf, dass die bisherige Achterbahnhöhe von 40 m von der neuen Bahn deutlich übertroffen wird.
Sagt ihm das Angebot zu?
Der Juniorchef ist als Ingenieur für die Sicherheit und den Energiebedarf der Bahn zuständig.
Er möchte, dass die mittlere Steigung der Aufstiegsstrecke, die für den Energiebedarf der Bahn maßgeblich ist, den Wert 1 nicht übersteigt.
Außerdem möchte er wissen, in welchen Punkten der Aufstiegsstrecke die lokale Steigung gleich der mittleren Steigung ist.
Berechne die jeweiligen Werte.
Aus Sicherheitsgründen für die Passagiere liegt ihm auch daran, dass im steilsten Punkt des Aufstiegs der lokale Steigungswinkel kleiner als 60° ist.
Hat er einen Einwand?
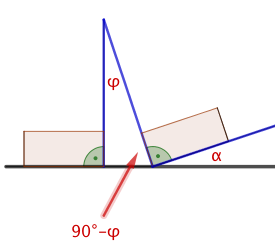
Außerdem möchte er sichergehen, dass der Neigungswinkel zwischen zwei knapp hintereinander gekoppelten Wagen kleiner als 25° ist, damit sich die Aufbauten der Wagen nicht berühren.
Er berechnet diesen Winkel für die Situation, bei der sich die Vorderachse des ersten Wagens am Punkt und die Hinterachse am Punkt befindet.
Wie groß ist dieser Winkel?
Die Enkelin des Seniorchefs ist als Marketingleiterin von der Idee der Herstellerfirma begeistert, unter die Aufstiegsstrecke von bis ein Werbebanner zu spannen.
Dessen Kosten veranschlagt der Hersteller mit 3000.-€ für die Befestigung und 8,50€ pro Quadratmeter für die Materialkosten. Die Familie ist allerdings nicht bereit, mehr als 10000.-€ für das Banner auszugeben.
Wird das Banner bestellt?
Die Urenkelin des Seniorchefs ist Abiturientin und empfiehlt der Familie eine bescheidenere Vegrößerung der Bahn.
Sie rät, eine Aufstiegsfunktion der Form
so zu wählen, dass sich als Startpunkt des Aufstiegsteils der Bahn und die größte lokale Steigung im Punkt mit einem Steigungswinkel von 45° ergibt.
Die Berechnung von g(x) bereitet ihr keine Probleme.
Welche Höhe hätte die neue Achterbahn nach ihrem Vorschlag?
- 2
Auf einem Streckenabschnitt soll eine Autobahnteilstrecke neu gebaut werden.
Durch Steigungen und Gefälle können Probleme für die Verkehrsteilnehmer entstehen.Deshalb werden beim Neubau von Autobahnen Steigungen über vermieden.
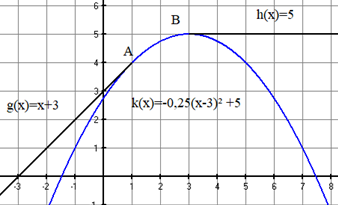
Das Steigungsprofil der geplanten Autobahnstrecke wird durch die Funktion beschrieben (siehe Figur 1).

Begründe rechnerisch, warum die neue Autobahnstrecke mit diesem Steigungsprofil nicht gebaut werden kann.
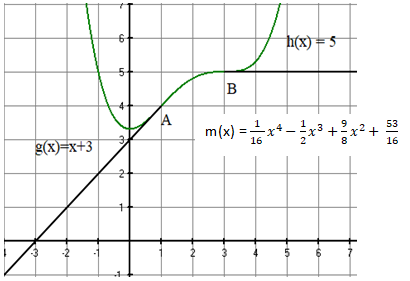
Im Intervall [-4;+4] soll die Autobahn daraufhin parabelförmig mit dem Höhenverlauf
untertunnelt werden (siehe Figur 2 und die Vergrößerung in Figur 3).

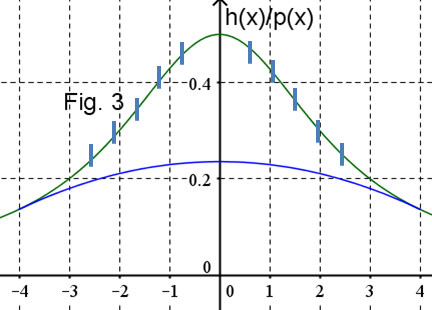
Kann die geplante Autobahnteilstrecke jetzt gebaut werden?
Bestätige deine Rechenergebnisse z.B. mithilfe von Geogebra graphisch.
- 3
Beim Neubau von Autobahnen werden Steigungen über 6% vermieden. Deshalb sind oft Untertunnelungen oder Geländeabtragungen nötig.
Bei dieser Aufgabe wird das Steigungsprofil der geplanten Autobahnstrecke durch die Funktion
beschrieben (siehe Fig. 1).
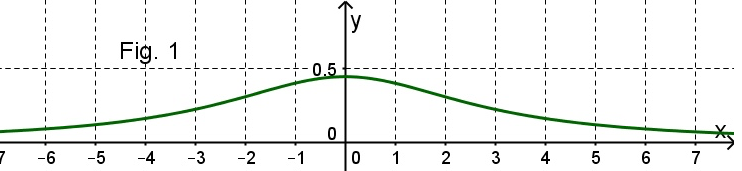
Begründe rechnerisch, warum die neue Autobahnstrecke mit diesem Steigungsprofil nicht gebaut werden kann.
Im Intervall [-2;+2] soll das Gelände daraufhin parabelförmig mit dem Höhenprofil
abgetragen werden (siehe die Fig.2 und die Vergrößerung in Fig.3)
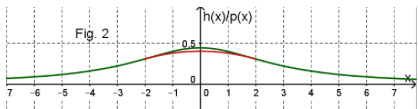
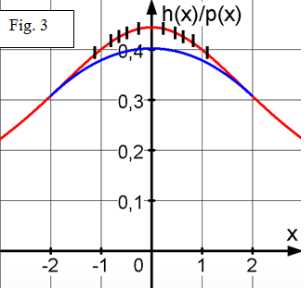
Kann die Autobahn jetzt gebaut werden?
Bestätige das Rechenergebnis graphisch, indem du z.B. in einem Geogebra-Applet die kritischen Steigungswerte überprüfst!
- 4
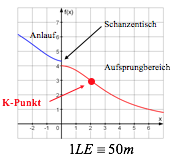
Das Aufsprungprofil einer Skisprungschanze wird näherungsweise durch folgende Funktion beschrieben:
Unter dem "K-Punkt" einer Sprungschanze versteht man den Aufsprungpunkt mit der geringsten Aufsprungbelastung für den Springer.
Berechne die horizontale Entfernung des K-Punktes vom Schanzentisch sowie den Neigungswinkel der Aufsprungbahn im K-Punkt.
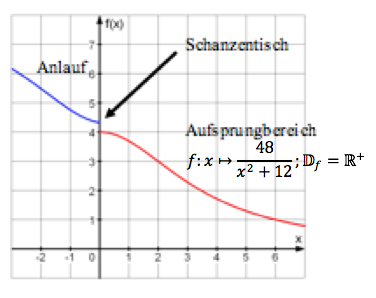
Maßstab der Zeichnung:
- 5
Eine Gemeinde möchte in einem Gebirgsmassiv, in dem sich eine waagrecht verlaufende, geologisch interessante Schicht befindet, ein kleines Museum errichten, welches Besuchern einen Einblick in die Besonderheiten der Gesteinsformation geben soll.
Geplant ist ein Ausstellungsraum mit Erklärungstafeln, Tonbildschau und ähnlichem, der sich ca. 500 m weit innerhalb des Berges befinden soll, und zu dem die Besucher mit einer kleinen Bahn hingebracht werden.
Die Bahnstrecke soll dabei so geführt werden, dass die Besucher während der Fahrt einen möglichst guten Einblick in die interessante Gesteinsschicht bekommen.
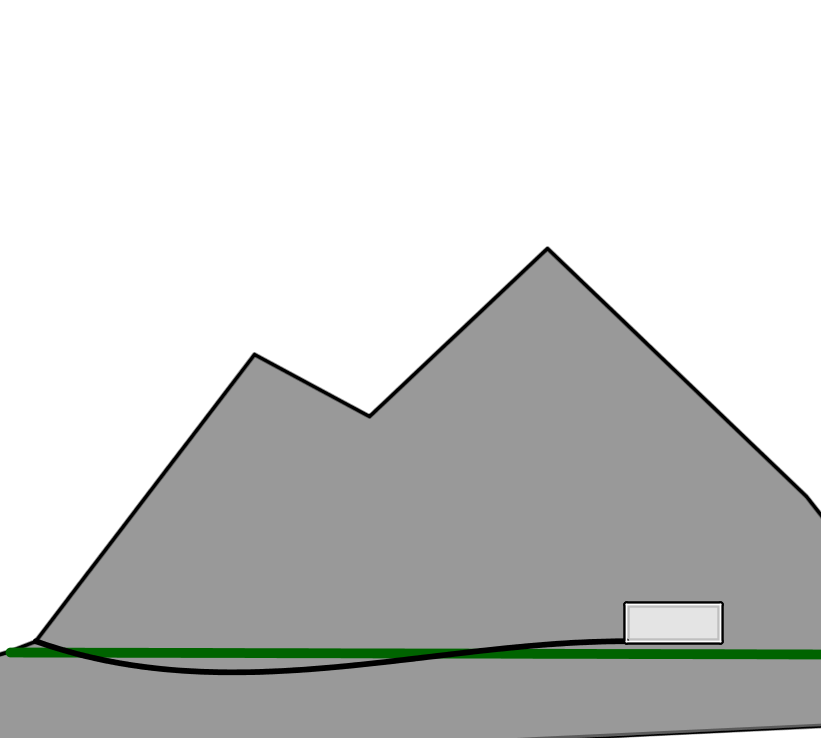
Skizze nicht maßstabsgetreu
Nach dem Architektenentwurf liegt der Punkt, in dem der Zug in den Berg hineinfahren soll, 1,55 m oberhalb der Höhe der Gesteinsschicht. Von dort aus verläuft die geplante Strecke in einer leicht geschwungenen Linie teils oberhalb, teils unterhalb der Schicht bis zu dem Ausstellungsraum.
Wählt man den oberen Rand der Gesteinsschicht als -Achse, und setzt am Einstiegspunkt der Bahn in den Berg , so wird der Höhenverlauf der Strecke für angenähert beschrieben durch die Funktion mit
wobei und in Metern gemessen werden.
Berechne den Neigungswinkel gegen die Horizontale, in dem der Zug im Punkt in den Berg einfährt.
Bestimme rechnerisch die Stelle , an der die Bahnstrecke ihren tiefsten Punkt erreicht. Runde dabei auf zwei Stellen hinter dem Komma. Wie tief unterhalb des unteren Randes der Gesteinsschicht liegt dieser Punkt, wenn die Gesteinsschicht ca. 80 cm dick ist? (Teilergebnis: )
Im Endpunkt fährt der Zug in den Ausstellungsraum ein. Begründe durch eine geeignete Rechnung, dass der Übergang von der geschwungenen Bahnstrecke auf den waagrecht liegenden Ausstellungsraum ohne Knick erfolgt.
Welche mittlere Steigung überwindet die Lokomotive zwischen dem tiefsten Punkt der Strecke und dem Endpunkt ? An welchen Stellen ist die lokale Steigung gerade genauso groß wie diese mittlere Steigung?
Welche Steigung muss die Lokomotive zwischen dem tiefsten Punkt und maximal bewältigen?
- 6
In zwei benachbarten Städten gibt es jeweils einen Kopf- oder Sackbahnhof.
In Stadt 1 befindet sich der Bahnhof am Punkt und in der Stadt 2 am Punkt .
Zum Punkt verlaufen die Gleise gemäß einer linearen Funktion . Die Gleise zum Punkt verlaufen gemäß .
Um die Bahnverbindungen in Deutschland weiter auszubauen, möchte die Deutsche Bahn die beiden Bahnhöfe mit einem Gleis verbinden.
Zeige, dass es keine quadratische Funktion zur Verbindung der beiden Bahnhöfe gibt. Die Anschlussstellen sollen versatzfrei und knickfrei sein.
Das Planungsbüro stellt der Projektleitung eine mögliche Gleisverbindung mit einer Funktion Grades vor. Das Ergebnis ist in Abbildung dargestellt.
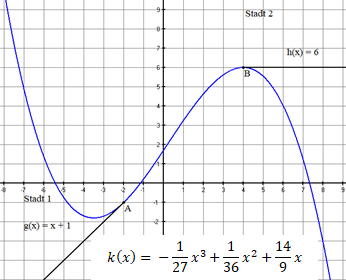
: Verbindung der Bahnhöfe mit einer kubischen Funktion
Ein Mitarbeiter der Projektleitung bemängelt die fehlende „Krümmungsruckfreiheit“ an den Übergangspunkten. Er weiß aus Erfahrung, dass eine Funktion Grades nie an zwei Punkten gleichzeitig krümmungsruckfrei sein kann.
Teilaufgabe 1. Zeige allgemein, dass er Recht hat.
Teilaufgabe 2. Weise dies auch rechnerisch für die angegebene Funktion und die Punkte und nach.
Das Planungsbüro der Bundesbahn hat nun eine Funktion Grades berechnet, die den Gleisverlauf beschreibt:
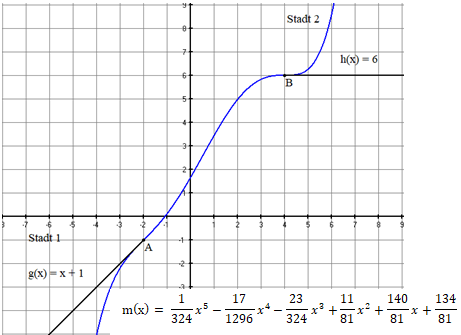
Graph der Funktion .
Erläutere anhand der Abbildung , dass die Krümmungsruckfreiheit im Punkt erfüllt ist.
Zeige rechnerisch, dass auch im Punkt ein krümmungsruckfreier Übergang möglich ist.
- 7
Zwischen zwei Stadtteilen befindet sich in der Nähe des Punktes ein Naturdenkmal.
Die Stadt möchte in zwei Bauabschnitten zunächst vom Stadtteil eine gerade Straße zum Punkt bauen. Im . Bauabschnitt soll dann eine Straßenverbindung von zum Punkt im Stadtteil gebaut werden.
Die Punkte und sollen durch eine quadratische Polynomfunktion versatzfrei und knickfrei miteinander verbunden werden.
Im Punkt endet eine Stichstraße mit der Gleichung
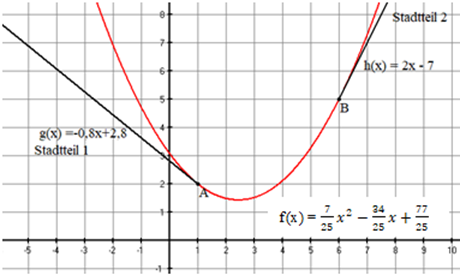
Planungsvorschläge des Ingenieurbüros für mögliche gerade Verbindungsstraßen vom Stadtteil bis zum Punkt .
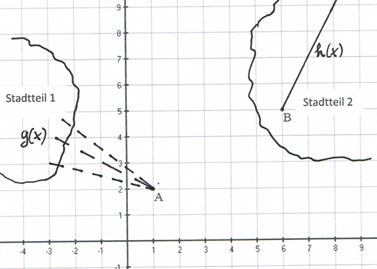
Bei der Berechnung der „Straßenfunktionen“ sind beide Bauabschnitte zu berücksichtigen.
Bestimme die Funktionsgleichungen der beiden Straßen und .
Zeichne die Funktionen und in ein Koordinatensystem.
Zeige, dass die in a) berechnete Funktion an den beiden
Anschlussstellen und einen Krümmungsruck erzeugt.
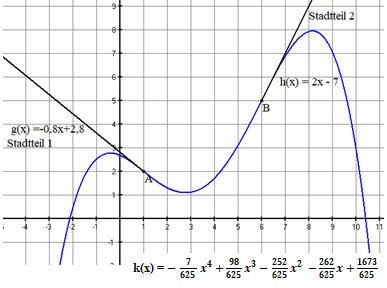
Um das Kriterium der „Krümmungsruckfreiheit“ in den beiden Punkten und zu erfüllen, sucht das Ingenieurbüro eine Funktion 4. Grades zur Verbindung der beiden Punkte unter Berücksichtigung der Straßen und .
Berechne die Funktion .
- 8
Trassierung
Zwischen zwei Stadtteilen befindet sich in der Nähe des Punktes ein Aussichtsturm.
Von Stadtteil 1 führt eine Stichstraße 1 bis zu diesem Punkt .
Im Stadtteil 2 endet eine Stichstraße 2 im Punkt .
Zur Verbindung der beiden Stadtteile soll eine Straße von nach gebaut werden.
Die Straße 1 ist für gegeben durch: .
Die Straße 2 ist für gegeben durch: .
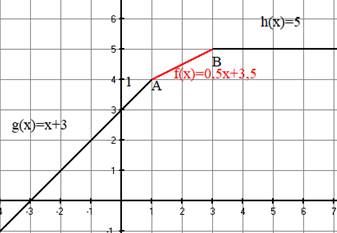
Gesucht ist eine lineare Funktion , die den Straßenverlauf zwischen den Punkten und beschreibt. An den Anschlussstellen soll kein „Versatz“ auftreten.
Zeichne die Funktionen und die berechnete Funktion in ein Koordinatensystem ein.
Beschreibe den Straßenverlauf an den beiden Übergangsstellen und .
Gesucht ist nun eine quadratische Funktion zur Verbindung der beiden Stichstraßen. Die Anschlussstellen sollen "versatzfrei" sein und keinen „Knick“ aufweisen sein.
Die Straßenbauingenieure sind immer noch nicht zufrieden. Sie stellen an den beiden Anschlussstellen fest, dass sich die Krümmung der Funktion an der Stelle von der Krümmung der Funktion unterscheidet bzw. an der Stelle von der Krümmung der Funktion unterscheidet.
Dadurch kommt es an den Übergangsstellen zu einem sogenannten „Krümmungsruck“.
Gesucht ist nun eine Funktion 4. Grades zur Verbindung der beiden Stichstraßen. Die Anschlussstellen sollen "versatzfrei" sein, keinen „Knick“ aufweisen und "krümmungsruckfrei"sein.
Hinweis: Ein „krümmungsruckfreier“ Übergang an einer Stelle bzw. ist möglich, wenn die Bedingungen bzw.
erfüllt sind.
- 9
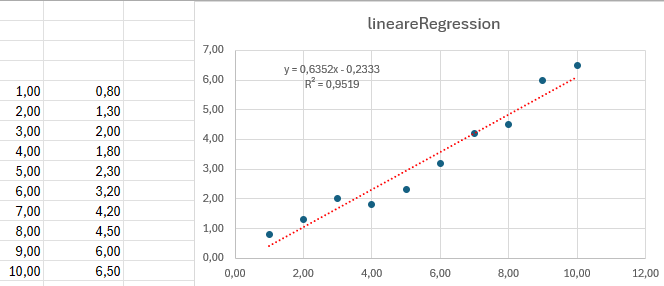
Bei einer Messung wurden folgende Datenpaare ermittelt:
Zeichne in ein Koordinatensystem ein Streudiagramm der Daten.
Zeichne nach Augenmaß eine Ausgleichsgerade ein und gib ihre Gleichung an.
Berechne mit einem Taschenrechner (z.B CASIO fx-991DE PLUS) oder mit Excel die Gleichung einer Regressionsgeraden. Gib auch den Korrelationskoeffizienten an.
Zeichne die mit dem TR berechnete Regressionsgerade in das Koordinatensystem aus Aufgabe b) ein und vergleiche die beiden Geraden.
Welchen y-Wert erwartet man für ?
Benutze die Gleichung der berechneten Regressionsgeraden.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?