Typisierung gewöhnlicher Differentialgleichungen

Differentialgleichungen (kurz: DGL) sind Gleichungen, in denen Ableitungen einer Funktion vorkommen.

Ziel ist es, diese Funktion zu ermitteln.

Was ist eine gewöhnliche Differentialgleichung?

Eine Gleichung, die eine oder mehrere Ableitungen einer gesuchten Funktion enthält, heißt Differentialgleichung (DGL).

Grob unterscheidet man zwischen partiellen Differentialgleichungen, bei denen partielle Ableitungen (d.h. Ableitungen einer Funktion, die mehrere Variablen besitzt) vorkommen und gewöhnlichen Differentialgleichungen, bei denen nur "normale" Ableitungen (d.h. Ableitungen einer Funktion mit nur einer Variable $x$ ) vorkommen.

Beispiel

partielle Differentialgleichung: $y (x, t) = 2 \frac{\partial^{2} y}{\partial t^{2}} - 4 \frac{\partial y}{\partial x}$
gewöhnliche Differentialgleichung: $y^{''} (x) - y^{'} (x) = 0$

Häufig wird das "gewöhnliche" weggelassen und nur von "Differentialgleichungen" gesprochen, obwohl eigentlich "gewöhnliche Differentialgleichungen" gemeint sind. Im Folgenden beschränken wir uns nur auf die gewöhnlichen Differentialgleichungen, die wir nunmehr ebenfalls nur "Differentialgleichungen" nennen.

Beachte

Eine Differentialgleichung kann eine oder mehrere Ableitungen der gesuchten Funktion $y (x)$ enthalten, die Funktion $y (x)$ selbst, sowie auch die Variable $x$ .

Beispiel:

Diese beiden Gleichungen sind Differentialgleichungen, weil sie jeweils Ableitungen der Funktion $y (x)$ enthalten:

$ y^{''} + x^{2} y^{'} + \cos x = 0$

$y^{'} - x = 9$

Anders als bei gewöhnlichen Gleichungen, bei denen die Variable (zum Beispiel $x$ ) für eine Zahl steht, ist die Unbekannte bei Differentialgleichungen kein Zahlenwert, sondern eine Funktionenschar. Diese Schar wird häufig mit $y (x)$ oder abgekürzt nur $y$ (bzw. $y^{'}$ für deren erste und $y^{''}$ für deren zweite Ableitung) bezeichnet.

	Lineare Gleichung	Differentialgleichung
Beispiel	$x - 4 = 2$	$2 y^{''} - 12 y^{'} + 10 y = 0$ (Hier treten Ableitungen der Schar $y$ auf)
Variable	Die Variable $x$ steht hierbei für eine reelle Zahl.	Die Funktionenschar $y$ ist gesucht.
Lösung	Nach kurzem Rechnen: $x = 6$	Mit mehr Rechnen: Jede Funktion der Form $y = C_{1} e^{x} + C_{2} e^{5 x}$ (mit $C_{1}, C_{2} \in ℝ$ ) ist eine Lösung.

Definition

Die Lösung einer Differentialgleichung ist also eine parametrisierte Funktion mit allgemeinen Parametern $C_{1}, C_{2}, . . . C_{n}$ . Diese Lösung heißt allgemeine Lösung, weil die Parameter noch nicht bestimmt sind. Setzt man für die Parameter spezielle Zahlenwerte ein, so erhält man eine spezielle Lösung der Differentialgleichung.

Beispiel

Sei $y = - \frac{1}{2} x^{2} + C_{1} x + C_{2}$ die allgemeine Lösung einer Differentialgleichung. Dann ergibt sich eine spezielle Lösung, wenn man beispielsweise $C_{1} = 3$ und $C_{2} = - 2$ setzt: $y = - \frac{1}{2} x^{2} + 3 x - 2$ ist also eine spezielle Lösung der Differentialgleichung.

Ordnung von Differentialgleichungen

Definition

Die Ordnung einer Differentialgleichung kannst du einfach an dem Grad $n$ der höchsten vorkommenden Ableitung ablesen. Man spricht dann von einer Differentialgleichung n-ter Ordnung.

Beispiel

$y^{''} + y^{'} = 8$ ist eine Differentialgleichung 2. Ordnung, weil die zweite Ableitung von $y (x)$ die höchste vorkommende ist

$y^{'} - y + x = 0$ ist eine Differentialgleichung 1. Ordnung, weil die höchste Ableitung die erste Ableitung $y^{'}$ ist.

Die allgemeine Lösung einer Differentialgleichung hat übrigens immer genau so viele Parameter $C_{1}, C_{2,} . . . C_{n}$ wie die Ordnung $n$ ist. Die Lösung einer Differentialrechnung 2. Ordnung hat also beispielsweise 2 Parameter.

Lineare und Nichtlineare Differentialgleichungen

Definition

Bei einer linearen Differentialgleichung tritt die Funktion $y$ und alle ihre Ableitungen nur in der ersten Potenz, also nicht als Produkt auf.

Beispiel

$y^{''} + {(y)}^{2} = 7$ ist nichtlinear, weil $y$ quadriert wird

$y^{''} \cdot y = 0$ ist nichtlinear, weil die Funktion $y$ mit ihrer zweiten Ableitung $y^{''}$ multipliziert wird

$y^{'} \cdot x + 7 = 0$ ist linear, weil $y^{'}$ nur mit $x$ , aber nicht mit der Funktion $y$ oder einer ihrer Ableitungen multipliziert wird

$y^{''} \cdot \sin (x) = 0$ ist - trotz des nichtlinearen Koeffizienten $\sin (x)$ - linear, solange nicht die Funktion $y$ selbst (oder eine ihrer Ableitungen) das Argument der nichtlinearen Funktion ist (d.h. solange $y$ nicht im Sinus/Kosinus bzw. in irgendeiner anderen nichtlinearen Funktion steht)

$y^{''} \cdot \sin (y) = y^{'}$ ist also nichtlinear, weil $y$ das Argument der nichtlinearen Funktion ist

Wichtige Sonderform: Lineare Differentialgleichung mit konstanten Koeffizienten

Definition

Eine lineare Differentialgleichung, bei der die gesuchte Funktion $y$ und ihre Ableitungen nur mit konstanten Koeffizienten, also reellen Zahlen (und nicht beispielsweise mit $x$ oder der Funktion $y$ ) multipliziert werden, heißt lineare Differentialgleichung mit konstanten Koeffizienten.

Die allgemeine - und sehr häufig vorkommende - Form einer linearen Differentialgleichung 2. Ordnung mit konstanten Koeffizienten sieht wie folgt aus:

a_{2} y^{''} + a_{1} y^{'} + a_{0} y

=

f (x)

Dabei sind alle Koeffizienten $a_{2}, a_{1}, a_{0}$ reelle Zahlen - nur muss $a_{2}$ ungleich Null sein, da sonst die Differentialgleichung nicht mehr 2. Ordnung wäre.

Beispiel:

2 y^{''} - 3 y^{'} + y

=

0

Homogene und inhomogene lineare Differentialgleichungen

Definition

Eine lineare Differentialgleichung ist zusätzlich homogen, wenn sie ausschließlich Glieder enthält, die die Funktion $y$ selbst oder eine ihre Ableitungen enthält - jedoch kommt kein Glied nur mit $x$ oder einer reellen Zahl vor. Sonst heißt die Differentialgleichung inhomogen.

Vorsicht

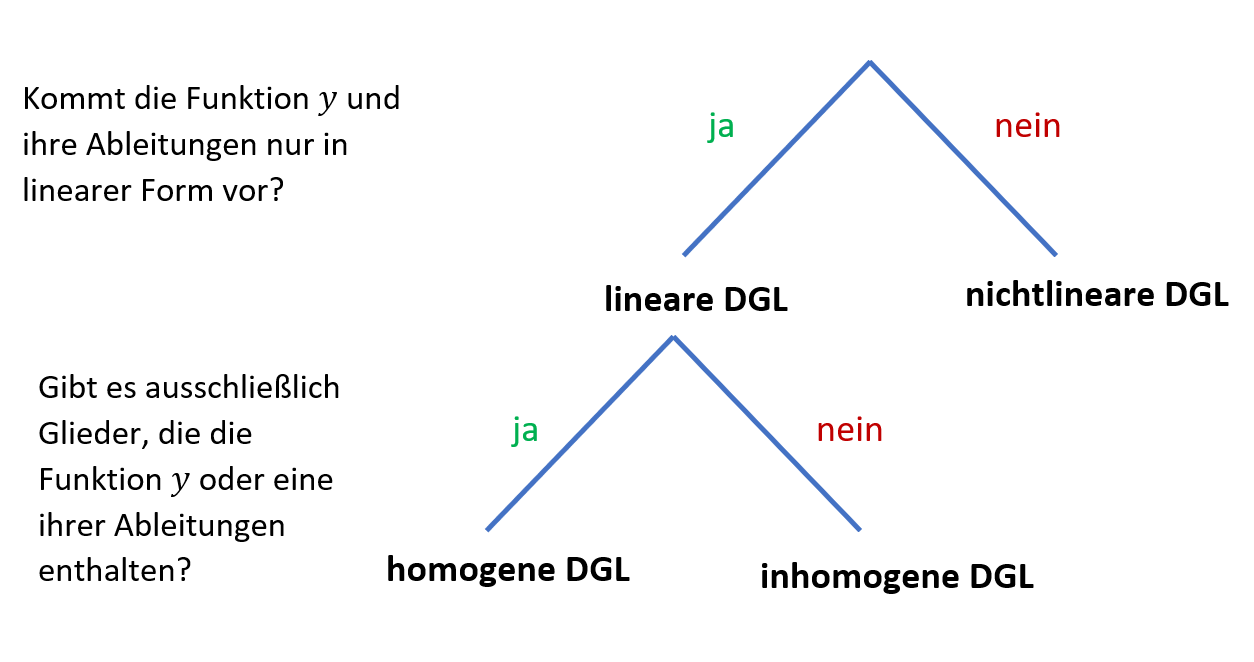
Diese Typisierung gilt nur für lineare Differentialgleichungen!

Für den Fall einer linearen Differentialgleichung 2. Ordnung mit konstanten Koeffizienten ist die folgende allgemeine Form homogen:

a_{2} y^{''} + a_{1} y^{'} + a_{0} y = 0

weil kein Glied ohne $y$ oder eine Ableitung von $y$ vorkommt. Rechts steht die Null.

Die folgende Form ist dagegen inhomogen:

a_{2} y^{''} + a_{1} y^{'} + a_{0} y = f (x)

weil rechts eine Funktion von $x$ steht (zum Beispiel $x + 4$ ) und es damit Glieder gibt, die nicht $y$ oder eine Ableitung von $y$ enthalten.

Beispiel:

$3 y^{''} - x y^{'} = x^{2}$ ist eine lineare inhomogene Differentialgleichung 2. Ordnung, weil das Glied $x^{2}$ nicht die Funktion $y$ oder eine ihrer Ableitungen enthält. Dieses Glied einer inhomogenen Differentialgleichung, also in diesem Fall $x^{2}$ , nennt man Störfunktion.

$y^{''} + x y^{'} - y = 0$ ist linear, homogen und 2. Ordnung, weil alle Glieder entweder $y, y^{'}$ oder $y^{''}$ enthalten.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?