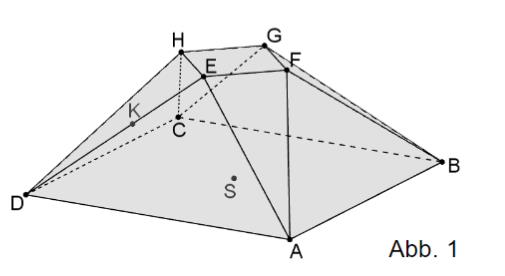
Der in Abbildung 1 dargestellte Körper wird begrenzt von der quadratischen Grundfläche mit und , acht dreieckigen Seitenflächen und einem weiteren Quadrat mit und . Der Mittelpunkt des Quadrats ist der Ursprung des Koordinatensystems und der gesamte Körper ist symmetrisch sowohl bezüglich der -Ebene als auch bezüglich der -Ebene.
Zeigen Sie, dass das Dreieck bei rechtwinklig ist. (2P)
Das Dreieck liegt in der Ebene . Ermitteln Sie eine Gleichung von in Koordinatenform und beschreiben Sie die besondere Lage von im Koordinatensystem. (4P)
(zur Kontrolle: )
Berechnen Sie die Größe des spitzen Winkels, den die Seitenfläche und die Grundfläche einschließen. (3P)
°Auf der Strecke gibt es einen Punkt für den gilt.
Bestimmen Sie die Koordinaten von . (4P)
ist der Mittelpunkt der Strecke . Begründen Sie, dass die Gerade den Innenwinkel des Dreiecks bei halbiert, und weisen Sie rechnerisch nach, dass auf der Gerade liegt. (4P)
Der Körper kann in neun Pyramiden zerlegt werden, von denen jede kongruent zu genau einer der drei Pyramiden , bzw. ist (vgl. Abbildung 2). Die Pyramide hat das Volumen und die Pyramide hat das Volumen . Bestimmen Sie das Volumen des gesamten Körpers. (4P)

Es gibt genau eine Kugel, auf der alle acht Eckpunkte des Körpers liegen. Ermitteln Sie die Koordinaten des Mittelpunkts dieser Kugel. (4P)
