Nachtermin Teil A - lernen mit Serlo!

Aufgabe A2

In der Zeichnung ist das Drachenviereck $A B C D$ mit der Symmetrieachse $A C$ dargestellt.

Es gilt: $A B = 10$ cm; $∢ B A D = 50 °$ ; $∢ C B A = 110 °$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

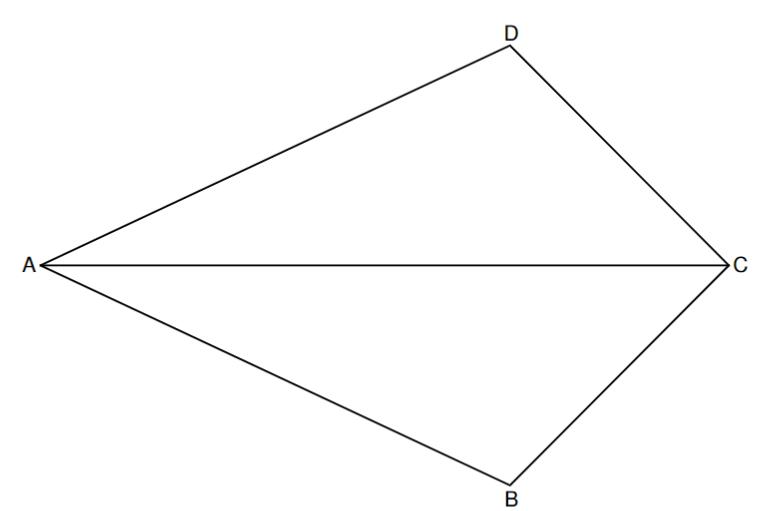
Punkte $E_{n}$ liegen auf der Strecke $[A C]$ und legen zusammen mit dem Punkt $B$ Strecken $[B E_{n}]$ fest. Die Winkel $E_{n} B A$ haben das Maß $φ$ mit $φ \in] 0 °; 110 °]$ . Zeichnen Sie die Strecke $[B E_{1}]$ für $φ = 15 °$ in die Zeichnung zu 2) ein und zeigen Sie durch Rechnung, dass für die Länge der Strecken $[B E_{n}]$ in Abhängigkeit von $φ$ gilt:
$B E_{n} (φ) = \frac{4,23}{\sin (φ + 25 °)} cm$ . (3 P)

Zeigen Sie durch Rechnung, dass für die Länge der Strecken $[B E_{n}]$ in Abhängigkeit von $φ$ gilt: $B E_{n} (φ) = \frac{4,23}{\sin (φ + 25 °)} cm$ .
Verwende den Sinussatz:
$\frac{B E_{n}}{\sin α} = \frac{A B}{\sin γ}$
$α = ∢ B A C = 0,5 \cdot 50^{\circ} = 25^{\circ}$
$γ = 180^{\circ} - (φ + α)$
$γ = 180^{\circ} - (φ + 25^{\circ})$
Dann folgt:
$\frac{B E_{n}}{\sin 25^{\circ}} = \frac{A B}{\sin (180^{\circ} - (φ + 25^{\circ}))}$
Mit $A B = 10 cm$ und $\sin (180^{\circ} - (φ + 25^{\circ})) = \sin (φ + 25^{\circ})$ erhält man dann:
$\frac{B E_{n}}{\sin 25^{\circ}} = \frac{10 cm}{\sin (φ + 25^{\circ})} \Rightarrow B E_{n} (φ) = \frac{\sin 25^{\circ} \cdot 10 cm}{\sin (φ + 25^{\circ})}$
$B E_{n} (φ) = \frac{4,23}{\sin (φ + 25^{\circ})} cm φ \in] 0 °; 110 °]$
Zeichnen Sie die Strecke $[B E_{1}]$ für $φ = 15 °$ in die Zeichnung ein:
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Das Dreieck $A B E_{2}$ ist gleichschenklig mit der Basis $[A B]$ . Berechnen Sie den Flächeninhalt des Dreiecks $A B E_{2} .$ (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt Dreieck
$A = 0,5 \cdot g \cdot h$
Es ist $g = A B = 10 cm$ .
Die Höhe $h$ wird mit Sinus berechnet:
$\sin ∢ E_{2} B A = \frac{h}{B E_{2}}$
$∢ E_{2} B A = ∢ B A C = 25^{\circ}$
$\Rightarrow h = B E_{2} \cdot \sin 25^{\circ}$
$B E_{2} (25^{\circ}) = \frac{4,23}{\sin (25^{\circ} + 25^{\circ})} = 5,52 cm$
Also ist $h = 5,52 \cdot \sin 25^{\circ} cm$
$\Rightarrow A_{A B E_{2}} = 0,5 \cdot g \cdot h = 0,5 \cdot 10 \cdot 5,52 \cdot \sin 25^{\circ} = 11,66 {cm}^{2}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Punkt $E_{3}$ ist der Mittelpunkt des Inkreises des Drachenvierecks $A B C D$ . Zeichnen Sie den Punkt $E_{3}$ sowie den Inkreis in die Zeichnung zu 2) ein und berechnen Sie den Radius $r$ des Inkreises. (4 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Drachenviereck
Der Punkt $E_{3}$ ist der Mittelpunkt des Inkreises des Drachenvierecks $A B C D$ .
Der Punkt $E_{3}$ und der Inkreis werden eingezeichnet.
Berechne $E_{3}$
Der Mittelpunkt des Inkreises ist der Schnittpunkt der Winkelhalbierenden.
Der Winkel $∢ C B A = 110 °$ . Dann ist der halbe Winkel $∢ C B E_{3} = 0,5 \cdot 110^{\circ} = 55^{\circ} .$
Die Strecke $B E_{3}$ berechnest Du mit:
$B E_{n} (φ)$ $=$ $= \frac{4,23}{\sin (φ + 25^{\circ})} cm$
↓
Setze $φ = 55^{\circ}$ ein.
$B E_{3} (55^{\circ})$ $=$ $\frac{4,23}{\sin (55^{\circ} + 25^{\circ})} cm$
$=$ $\frac{4,23}{\sin (80^{\circ})} cm$
$=$ $4,30 cm$
Berechne r
In dem oben eingezeichneten rechtwinkligen Dreieck gilt:
$\sin ∢ C B E_{3} = \frac{r}{B E_{3}} \Rightarrow r = B E_{3} \cdot \sin ∢ C B E_{3}$
Dabei ist $r$ der Radius des Inkreises.
$r$ $=$ $B E_{3} \cdot \sin ∢ C B E_{3}$
↓
Setze $B E_{3} = 4,30 cm$ und $∢ C B E_{3} = 55^{\circ}$ ein.
$=$ $4,30 \cdot \sin 55^{\circ} cm$
$=$ $3,52 cm$
Den Radius $r$ des Inkreises beträgt $3,52 cm$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

$B E_{n} (φ)$	$=$	$= \frac{4,23}{\sin (φ + 25^{\circ})} cm$
	↓	Setze $φ = 55^{\circ}$ ein.
$B E_{3} (55^{\circ})$	$=$	$\frac{4,23}{\sin (55^{\circ} + 25^{\circ})} cm$
	$=$	$\frac{4,23}{\sin (80^{\circ})} cm$
	$=$	$4,30 cm$

$r$	$=$	$B E_{3} \cdot \sin ∢ C B E_{3}$
	↓	Setze $B E_{3} = 4,30 cm$ und $∢ C B E_{3} = 55^{\circ}$ ein.
	$=$	$4,30 \cdot \sin 55^{\circ} cm$
	$=$	$3,52 cm$

Aufgabe A2

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechne E3

Berechne r

Hast du eine Frage oder Feedback?

Berechne $E_{3}$