Nachtermin Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

In zwei Stromkreisen wird je eine Spule von Gleichstrom durchflossen. Wenn ein Stromkreis geöffnet wird, klingt die entsprechende Stromstärke exponentiell ab. Der Zusammenhang zwischen der Zeit $x$ s nach dem Öffnen des Stromkreises und der Stromstärke $y$ mA kann bei Spulen näherungsweise durch eine Funktion mit einer Gleichung der Form $y=y_0\cdot k^x$ beschrieben werden, wobei $y_{0}$ mA die Stromstärke für $x = 0$ darstellt. (⁣ $\mathbb{G}=\mathbb{R_0^+\times \mathbb{R_0^+}}$ ; $y_0\in \mathbb{R_0^+}$ ; $k\in\mathbb{R^+}$ ).

Für die erste Spule ergeben sich folgende Werte:

Zeigen Sie rechnerisch, dass für diese Spule auf zwei Stellen nach dem Komma gerundet gilt: $k = 0, 22$ . Geben Sie sodann die zugehörige Funktionsgleichung an.

(2P)

Um wie viel Prozent verringert sich die Stromstärke bei der Spule aus 1a) pro Sekunde?
Die Stromstärke verringert sich pro Sekunde um ______ $%$
(1P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum (bzw. exponentieller Zerfall)
Bei der gegebenen Spule ist $k = 0, 22$ , d.h. es handelt sich um exponentielle Abnahme.
Die Stromstärke verringert sich pro Sekunde um $p=1-0{,}22=0{,}78=78\;\%$ .
Hinweis: Die Berechnung der prozentualen Abnahme kann auch mithilfe der Messwerte erfolgen.
Z. B. mit den Messwerten $2$ und $3$ : $p=\dfrac{218-48}{218}\approx 0{,}78=78\;\%$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Für die zweite Spule gilt: $k = 0, 25.$ Bei dieser wird gleichzeitig mit der Spule aus 1a) der Stromkreis geöffnet. Nach $3$ s ergeben sich für beide Spulen die gleichen Stromstärken. Berechnen Sie die Stromstärke der zweiten Spule in dem Moment, in dem die Stromkreise geöffnet werden.

(2P)

Aufgabe A2

In der Zeichnung ist das Drachenviereck $ABCD\$ mit der Symmetrieachse $A C$ dargestellt.

Es gilt: $\overline{AB}=10$ cm; $\sphericalangle BAD=50°$ ; $\sphericalangle CBA=110°$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

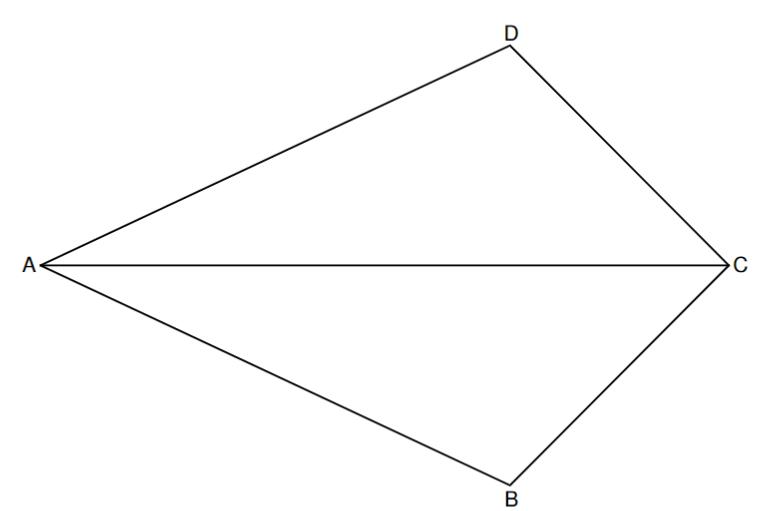
Punkte $E_{n}$ liegen auf der Strecke $[A C]$ und legen zusammen mit dem Punkt $B$ Strecken $[B E_{n}]$ fest. Die Winkel $E_{n} B A$ haben das Maß $\varphi$ mit $\varphi\in]0°;110°]$ . Zeichnen Sie die Strecke $[B E_{1}]$ für $\varphi=15°$ in die Zeichnung zu 2) ein und zeigen Sie durch Rechnung, dass für die Länge der Strecken $[B E_{n}]$ in Abhängigkeit von $\varphi$ gilt:
$\overline{BE_n}(\varphi)=\frac{4{,}23}{\sin(\varphi+25°)}\;\text{cm}$ . (3 P)

Zeigen Sie durch Rechnung, dass für die Länge der Strecken $[B E_{n}]$ in Abhängigkeit von $\varphi$ gilt: $\overline{BE_n}(\varphi)=\dfrac{4{,}23}{\sin(\varphi+25°)}\;\text{cm}$ .
Verwende den Sinussatz:
$\dfrac{\overline{BE_n}}{\sin\alpha}=\dfrac{\overline{AB}}{\sin\gamma}$
$\alpha=\sphericalangle \;BAC=0{,}5\cdot 50^\circ=25^\circ$
$\gamma=180^\circ-(\varphi+\alpha)$
$\gamma=180^\circ-(\varphi+25^\circ)$
Dann folgt:
$\dfrac{\overline{BE_n}}{\sin25^\circ}=\dfrac{\overline{AB}}{\sin(180^\circ-(\varphi+25^\circ))}$
Mit $\overline{AB}=10\;\text{cm}$ und $\sin(180^\circ-(\varphi+25^\circ))=\sin(\varphi+25^\circ)$ erhält man dann:
$\dfrac{\overline{BE_n}}{\sin25^\circ}=\dfrac{ 10\;\text{cm}}{\sin(\varphi+25^\circ)}\;\Rightarrow\;\overline{BE_n}(\varphi)=\dfrac{ \sin25^\circ\cdot 10\;\text{cm}}{\sin(\varphi+25^\circ)}$
Zeichnen Sie die Strecke $[B E_{1}]$ für $\varphi=15°$ in die Zeichnung ein:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Das Dreieck $A B E_{2}$ ist gleichschenklig mit der Basis $[A B]$ . Berechnen Sie den Flächeninhalt des Dreiecks $A B E_{2} .$ (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt Dreieck
$A=0{,}5\cdot g\cdot h$
Es ist $g= \overline{AB}=10\;\text{cm}$ .
Die Höhe $h$ wird mit Sinus berechnet:
$\sin\sphericalangle\;E_2BA=\dfrac{h}{\overline{BE_2}}$
$\sphericalangle\;E_2BA=\sphericalangle\;BAC=25^\circ$
$\Rightarrow\;h=\overline{BE_2}\cdot \sin25^\circ$
$\overline{BE_2}(25^\circ)=\dfrac{ 4{,}23}{\sin(25^\circ+25^\circ)}=5{,}52\;\text{cm}$
Also ist $h=5{,}52\cdot \sin25^\circ\;\text{cm}$
$\Rightarrow\;A_{ABE_2}=0{,}5\cdot g\cdot h=0{,}5\cdot 10\cdot 5{,}52\cdot \sin25^\circ=11{,}66\;\text{cm}^2$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Der Punkt $E_{3}$ ist der Mittelpunkt des Inkreises des Drachenvierecks $A B C D$ . Zeichnen Sie den Punkt $E_{3}$ sowie den Inkreis in die Zeichnung zu 2) ein und berechnen Sie den Radius $r$ des Inkreises. (4 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Drachenviereck

Der Punkt $E_{3}$ ist der Mittelpunkt des Inkreises des Drachenvierecks $A B C D$ .

Der Punkt $E_{3}$ und der Inkreis werden eingezeichnet.

Berechne $E_{3}$

Der Mittelpunkt des Inkreises ist der Schnittpunkt der Winkelhalbierenden.

Der Winkel $\sphericalangle CBA=110°$ . Dann ist der halbe Winkel $\sphericalangle \;CBE_3 =0{,}5\cdot 110^\circ=55^\circ.$

Die Strecke $\overline{BE_3}$ berechnest Du mit:

$\displaystyle \overline{BE_n}(\varphi)$	$=$	$\displaystyle =\dfrac{ 4{,}23}{\sin(\varphi+25^\circ)}\;\text{cm}$
	↓	Setze $\varphi=55^\circ$ ein.
$\displaystyle \overline{BE_3}(55^\circ)$	$=$	$\displaystyle \dfrac{ 4{,}23}{\sin(55^\circ+25^\circ)}\;\text{cm}$
	$=$	$\displaystyle \dfrac{ 4{,}23}{\sin(80^\circ)}\;\text{cm}$
	$=$	$\displaystyle 4{,}30\;\text{cm}$

Berechne r

In dem oben eingezeichneten rechtwinkligen Dreieck gilt:

$\sin\sphericalangle \;CBE_3 =\dfrac{r}{\overline{BE_3}}\;\Rightarrow\;r=\overline{BE_3}\cdot \sin\sphericalangle \;CBE_3$

Dabei ist $r$ der Radius des Inkreises.

$\displaystyle r$	$=$	$\displaystyle \overline{BE_3}\cdot \sin\sphericalangle \;CBE_3$
	↓	Setze $\overline{BE_3}=4{,}30\;\text{cm}$ und $\sphericalangle \;CBE_3 =55^\circ$ ein.
	$=$	$\displaystyle 4{,}30\cdot \sin55^\circ\;\text{cm}$
	$=$	$\displaystyle 3{,}52\;\text{cm}$

Den Radius $r$ des Inkreises beträgt $3{,}52\;\text{cm}$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Aufgabe A3

Das Drachenviereck $A B C D$ mit dem Diagonalenschnittpunkt $M$ ist die Grundfläche der Pyramide $A B C D S$ mit der Höhe $[M S]$ . Die Zeichnung zeigt ein Schrägbild der Pyramide $A B C D S$ , wobei $[A C]$ auf der Schrägbildachse liegt.

Es gilt: $\overline{AC}=6$ cm; $\overline{AM}=4$ cm; $\overline{BD}=6$ cm; $\overline{MS}=5$ cm.

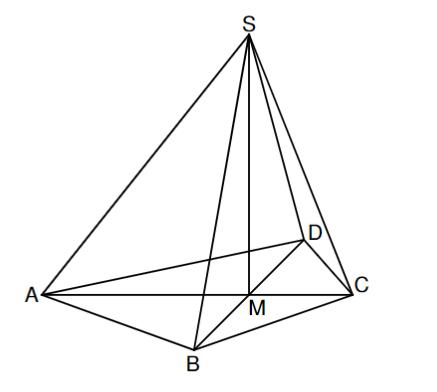
Der Punkt $E$ liegt auf der Halbgeraden $[A C$ mit $\overline{AE}=7{,}5$ cm. Punkte $P_{n}$ liegen auf der Strecke $[M S]$ . Die Winkel $M A P_{n}$ haben das Maß $\varphi$ . Die Punkte $P_{n}$ sind für $\varphi\in]0^\circ;51{,}34^\circ]$ die Spitzen von Pyramiden $A B E D P_{n}$ mit dem Drachenviereck $A B E D$ als Grundfläche sowie den Höhen $[M P_{n}]$ .
Zeichnen Sie die Pyramide $A B E D P_{1}$ für $\varphi=30°$ in das Schrägbild zu 3) ein. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Einzeichnen der Pyramide $A B E D P_{1}$ für $\varphi=30°$ in das Schrägbild.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechnen Sie das Volumen $V$ der Pyramiden $A B E D P_{n}$ in Abhängigkeit von $\varphi$ . (2 P)
[Ergebnis: $V(\varphi)=30\cdot\tan\varphi$ $c m^{3}$ ].

Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Das Pyramidenvolumen berechnet man mit:
$V=\dfrac{1}{3}\cdot G\cdot h$
Die Grundfläche ist ein Drachenviereck. Hier gilt für den Flächeninhalt:
$A_{\text{Drachenviereck}}=\dfrac{1}{2}\cdot e\cdot f$
Dabei sind $e$ und $f$ die Diagonalen des Drachenvierecks.
Damit folgt für das Pyramidenvolumen:
$V_{ABED{P_n}}=\dfrac{1}{3}\cdot \dfrac{1}{2}\cdot e\cdot f\cdot h=\dfrac{1}{3}\cdot \dfrac{1}{2}\cdot \overline{AE}\cdot \overline{BD}\cdot \overline{MP_n}$
Berechne $\overline{MP_n}$ :
Gegeben ist $\overline{AM}=4\;\text{cm}$ .
Dann gilt: $\tan\varphi=\dfrac{\overline{MP_n}}{4\;\text{cm}}\;$
$\Rightarrow\;\overline{MP_n}=4\cdot\tan\varphi\;\text{cm}$
mit $\varphi\in]0^\circ;51{,}34^\circ]$
Setze die gegebenen Werte $\overline{AE}=7{,}5 \;\text{cm}$ , $\overline{BD}=6\;\text{cm}$ und $\overline{MP_n}$ in $V$ ein:
$V(\varphi)=\dfrac{1}{3}\cdot \dfrac{1}{2}\cdot 7{,}5\cdot 6\cdot 4\cdot\tan\varphi\;\text{cm}^3=30\cdot\tan\varphi\;\text{cm}^3$
$V(\varphi)=30\cdot\tan\varphi\;\text{cm}^3$ mit $\varphi\in]0^\circ;51{,}34^\circ]$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Das Volumen der Pyramide $A B E D P_{2}$ ist genau so groß wie das Volumen der Pyramide $A B C D S$ . Bestimmen Sie den zugehörigen Wert für $\varphi$ . (2 P)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle y$	$=$	$\displaystyle 4500\cdot k^x$
	↓	Setze $(2 ∣ 218)$ ein.
$\displaystyle 218$	$=$	$\displaystyle 4500\cdot k^2$	$\displaystyle :4500$
	↓	Löse nach $k$ auf.
$\displaystyle \dfrac{218}{4500}$	$=$	$\displaystyle k^2$	$\displaystyle \sqrt{}$
$\displaystyle k_{1{,}2}$	$=$	$\displaystyle \pm \sqrt{\dfrac{218}{4500}}$
	$\approx ≈$	$\displaystyle \pm 0{,}22$

$\displaystyle y$	$=$	$\displaystyle y_0\cdot 0{,}25^x$
	↓	Setze den Messwert $(3 ∣ 48)$ ein.
$\displaystyle 48$	$=$	$\displaystyle y_0\cdot 0{,}25^3$	$\displaystyle :0{,}25^3$
	↓	Löse nach $y_{0}$ auf.
$\displaystyle \dfrac{48}{0{,}25^3}$	$=$	$\displaystyle y_0$
$\displaystyle y_0$	$=$	$\displaystyle 3072$

$\displaystyle 30\cdot\tan\varphi$	$=$	$\displaystyle 30$	$\displaystyle :30$
$\displaystyle \tan\varphi$	$=$	$\displaystyle 1$	$\displaystyle \tan^{-1}$
$\displaystyle \varphi$	$=$	$\displaystyle 45^\circ$

Nachtermin Teil A

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Aufgabe A2

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechne E3E_3E3​

Berechne r

Hast du eine Frage oder Feedback?

Aufgabe A3

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechne $E_{3}$