Die nachfolgende Abbildung zeigt den Graphen einer Normalparabel .
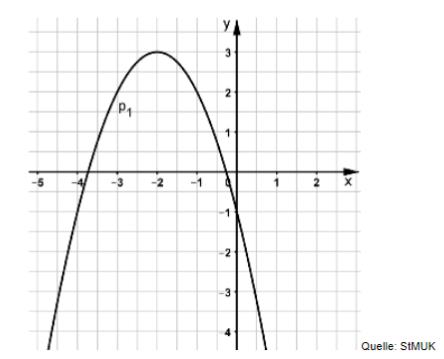
Ermitteln Sie rechnerisch die Funktionsgleichung von in der Normalform.
Überprüfen Sie durch Rechnung, ob die Punkte und auf der Normalparabel mit der Funktionsgleichung : liegen.
Ermitteln Sie rechnerisch den Scheitelpunkt der Parabel .
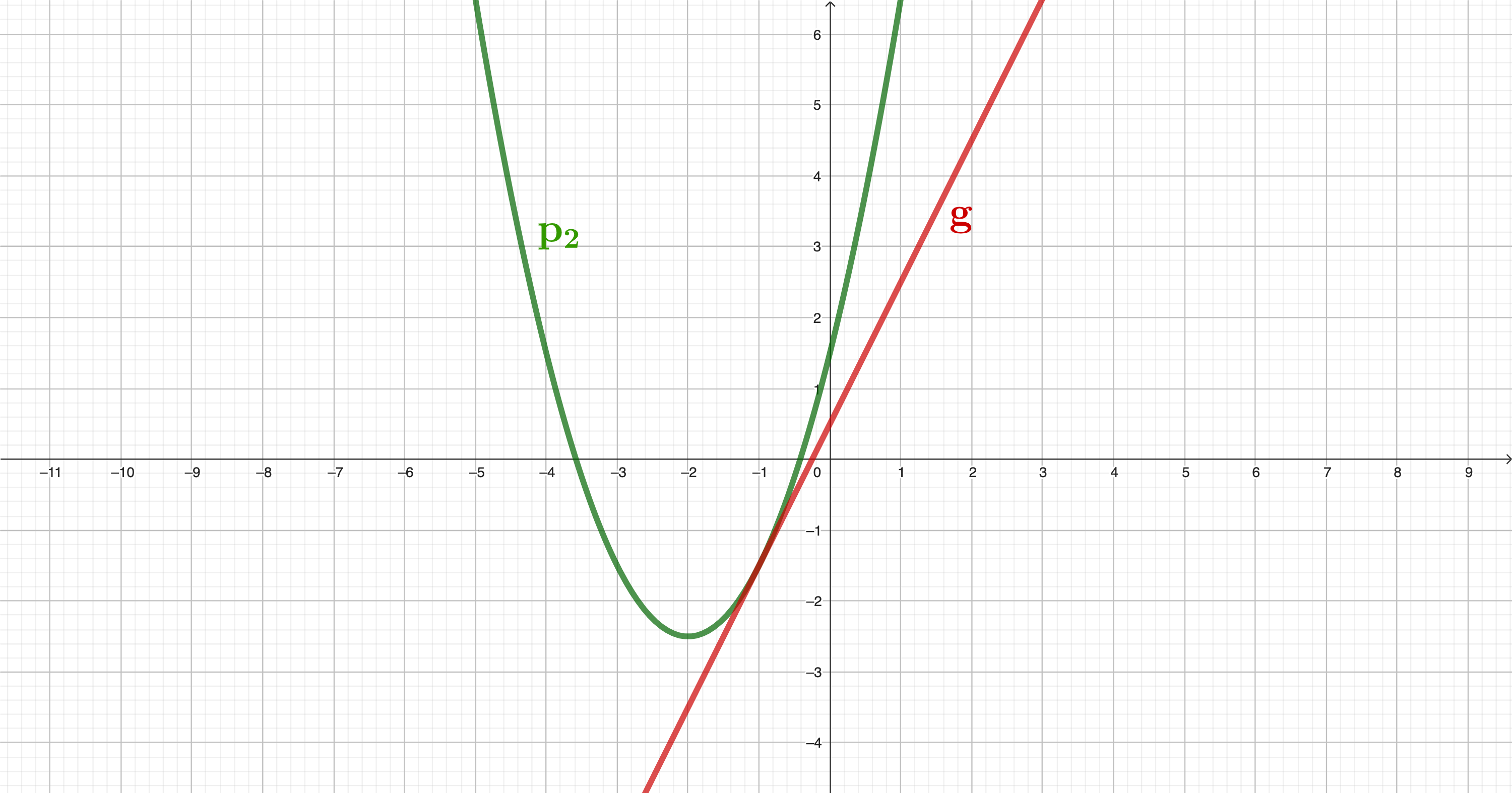
Die Gerade g mit der Funktionsgleichung hat mit der Parabel den Punkt gemeinsam. Berechnen Sie die Koordinaten von und geben Sie diesen Punkt an.
Zeichnen Sie die Graphen der Parabel und der Geraden in ein Koordinatensystem mit der Längeneinheit .
Eine nach unten geöffnete Normalparabel hat den Scheitelpunkt . Durch Spiegelung an der y-Achse entsteht . Durch eine weitere Spiegelung von an der x-Achse entsteht . Geben Sie die Funktionsgleichung der Parabel in der Scheitelpunktform an und stellen Sie Ihren Lösungsweg nachvollziehbar dar.