Gegeben ist der Graph der Funktion .
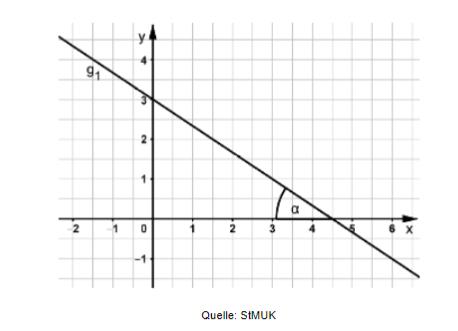
Geben Sie die Funktionsgleichung der Geraden an.
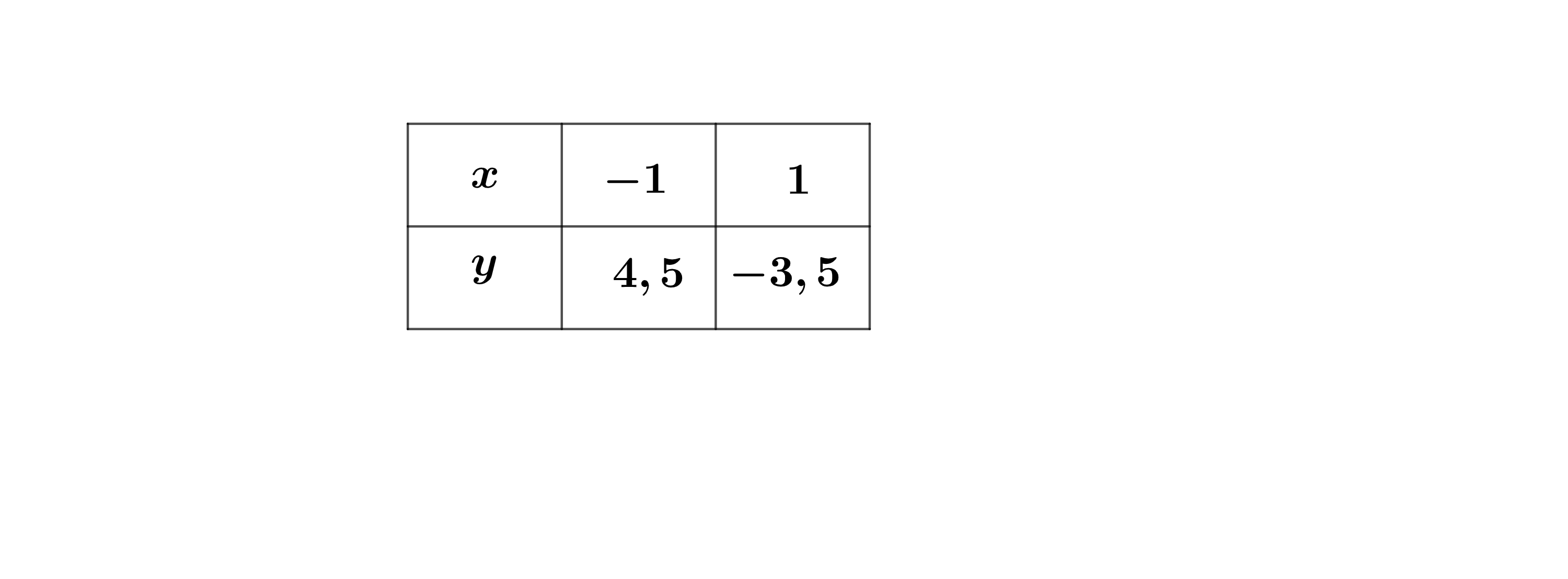
Die Gerade verläuft durch die Punkte und . Bestimmen Sie die Funktionsgleichung der Geraden rechnerisch.
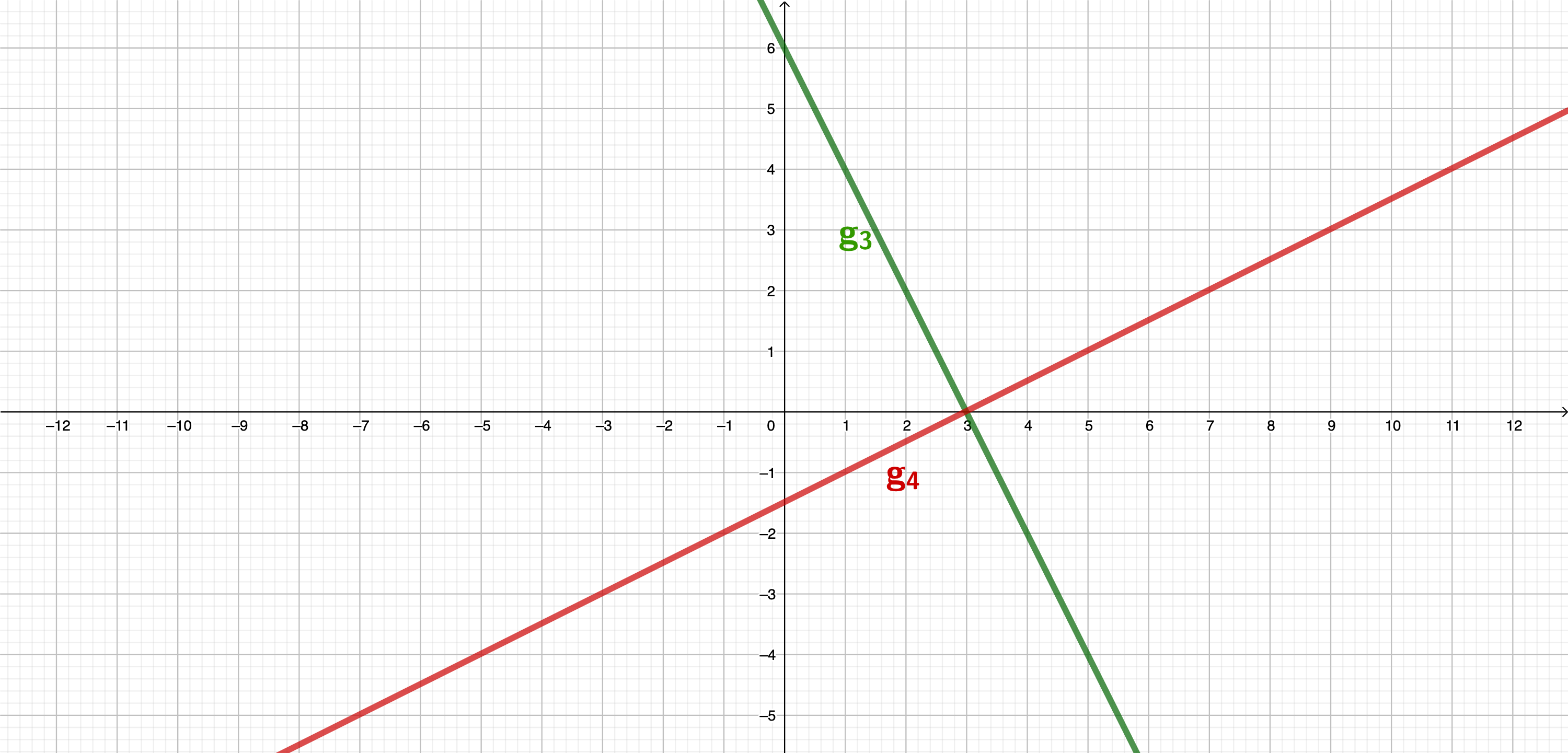
Die Gerade : schneidet die Gerade : im Punkt . Bestimmen Sie die Koordinaten dieses Schnittpunkts rechnerisch und geben Sie den Punkt an.
Überprüfen Sie rechnerisch, ob der Punkt auf der Geraden liegt.
Zeichnen Sie die Geraden und in ein Koordinatensystem.
Bestimmen Sie rechnerisch die Koordinaten des Schnittpunkts der Geraden : mit der x-Achse und geben Sie an.
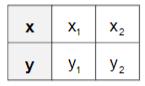
Erstellen Sie eine Wertetabelle mit 2 Wertepaaren zur Geraden . Es soll gelten:
Berechnen Sie den Winkel α (siehe Zeichnung).