Aufgabengruppe II
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
(Kleine Änderungen der Formulierung aufgrund der Umwandlung in ein digitales Medium sind kursiv geschrieben.)
- 1
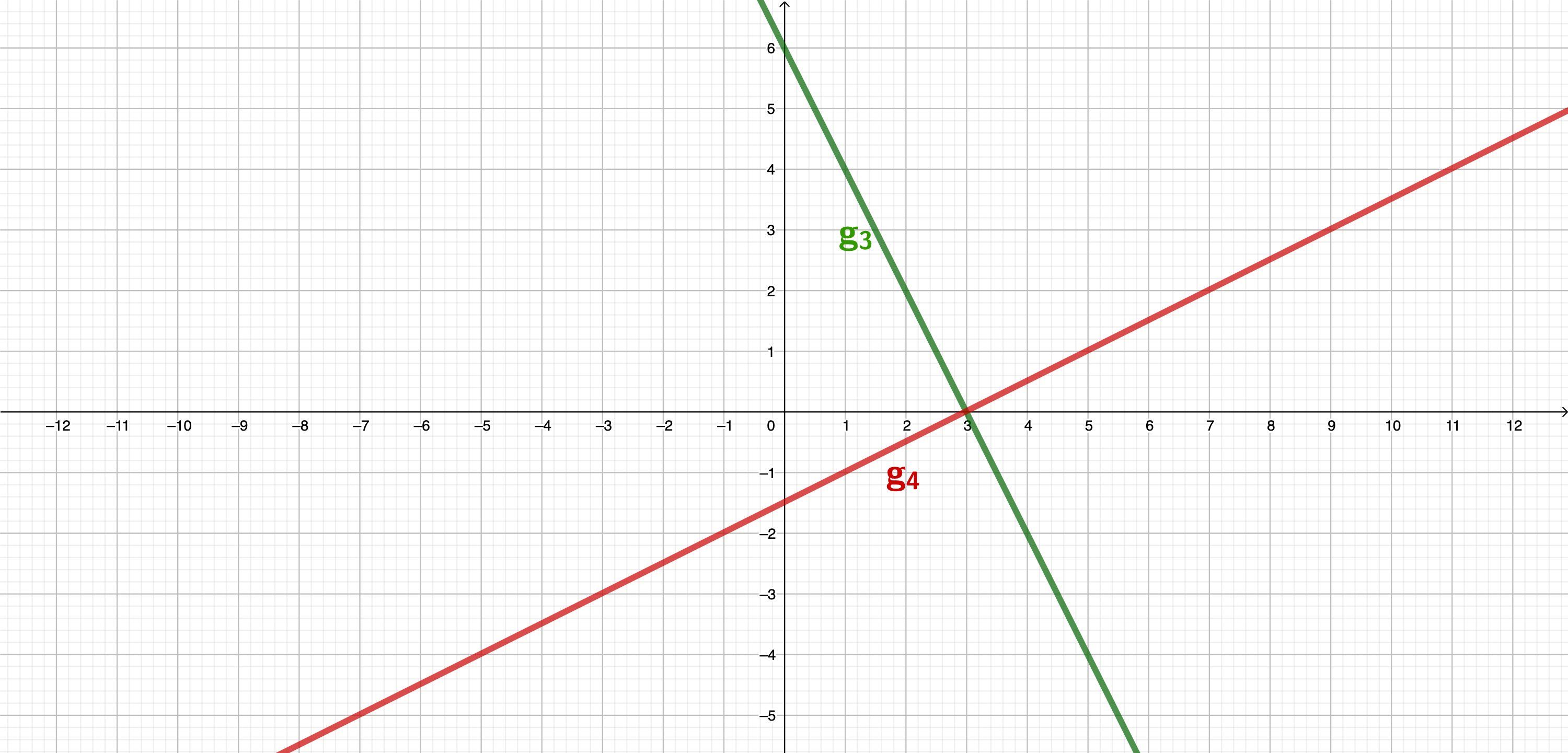
Gegeben ist der Graph der Funktion .
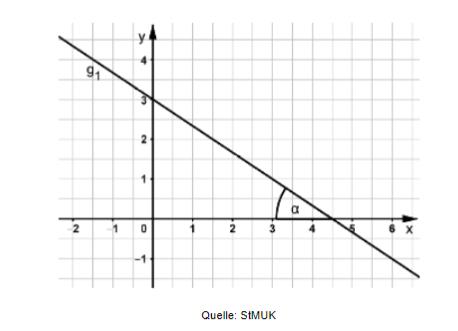
Geben Sie die Funktionsgleichung der Geraden an.
Die Gerade verläuft durch die Punkte und . Bestimmen Sie die Funktionsgleichung der Geraden rechnerisch.
Die Gerade : schneidet die Gerade : im Punkt . Bestimmen Sie die Koordinaten dieses Schnittpunkts rechnerisch und geben Sie den Punkt an.
Überprüfen Sie rechnerisch, ob der Punkt auf der Geraden liegt.
Zeichnen Sie die Geraden und in ein Koordinatensystem.
Bestimmen Sie rechnerisch die Koordinaten des Schnittpunkts der Geraden : mit der x-Achse und geben Sie an.
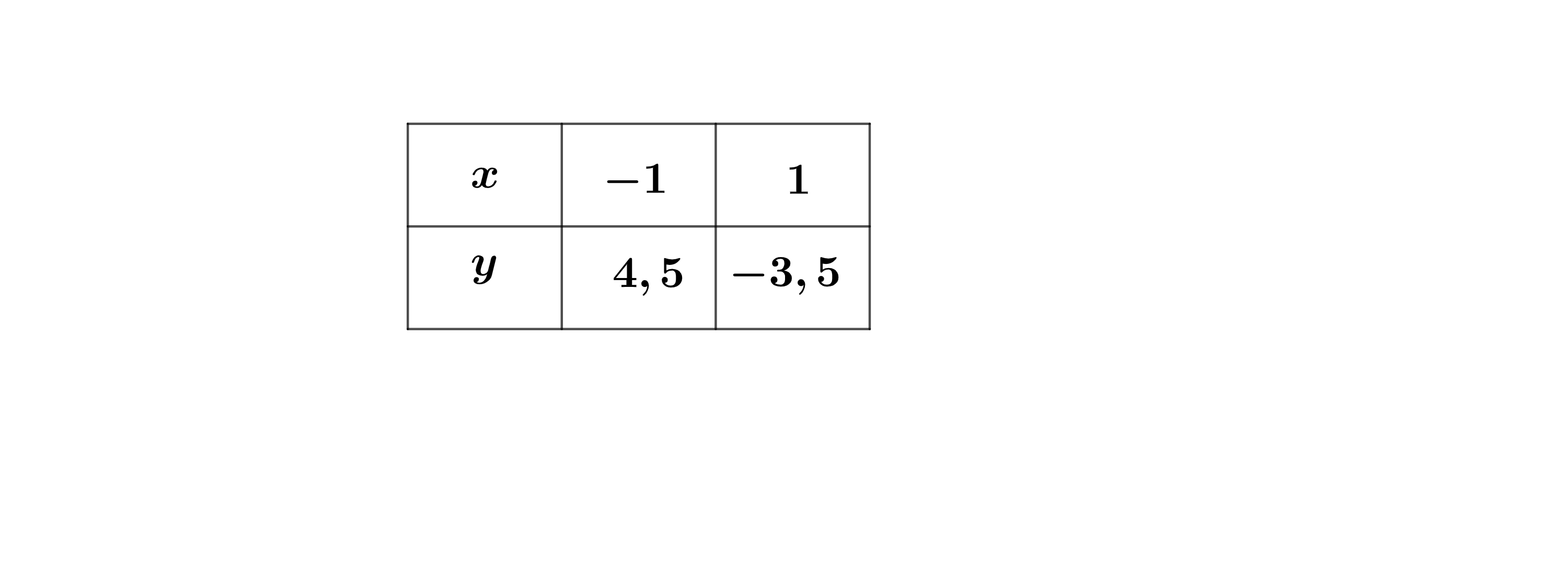
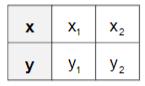
Erstellen Sie eine Wertetabelle mit 2 Wertepaaren zur Geraden . Es soll gelten:
Berechnen Sie den Winkel α (siehe Zeichnung).
- 2
Lösen Sie die folgende Gleichung rechnerisch. Geben Sie die Definitionsmenge und die Lösungsmenge an.
- 3
Lösen Sie folgende Aufgaben.
Familie Wegmann kauft ein neues Wohnmobil für 50 000 . Berechnen Sie den Wert dieses Wohnmobils nach sechs Jahren, wenn dieser in den ersten zwei Jahren um jeweils 9 % und in den darauf folgenden vier Jahren um jeweils 8% abnimmt.
Familie Grün kauft sich ein zwölf Jahre altes Wohnmobil zu einem Preis von
19 500 €. Bestimmen Sie den durchschnittlichen prozentualen Wertverlust pro Jahr, wenn der Neupreis des Wohnmobils 45000 € betrug.
Ab einem Alter von zwölf Jahren beträgt der durchschnittliche jährliche Wertverlust von Wohnmobilen 6,6 %.
Ermitteln Sie rechnerisch, nach wie vielen Jahren Familie Grün ihr Wohnmobil verkaufen müsste, um noch mindestens die Hälfte des Kaufpreises von 19500 € zu erhalten.
- 4
In nachstehender Skizze gilt:
, ,
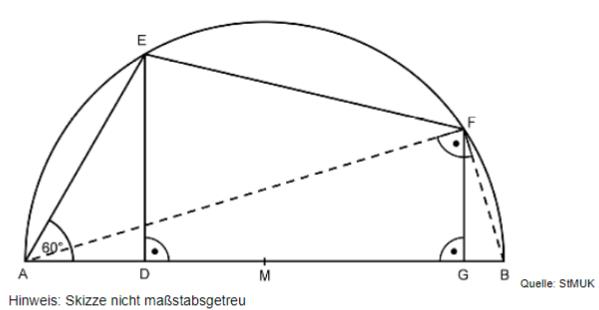
Berechnen Sie den Flächeninhalt des Trapezes .
Bestimmen Sie rechnerisch den Umfang des Trapezes .
- 5
Lösen Sie die folgenden Aufgaben.
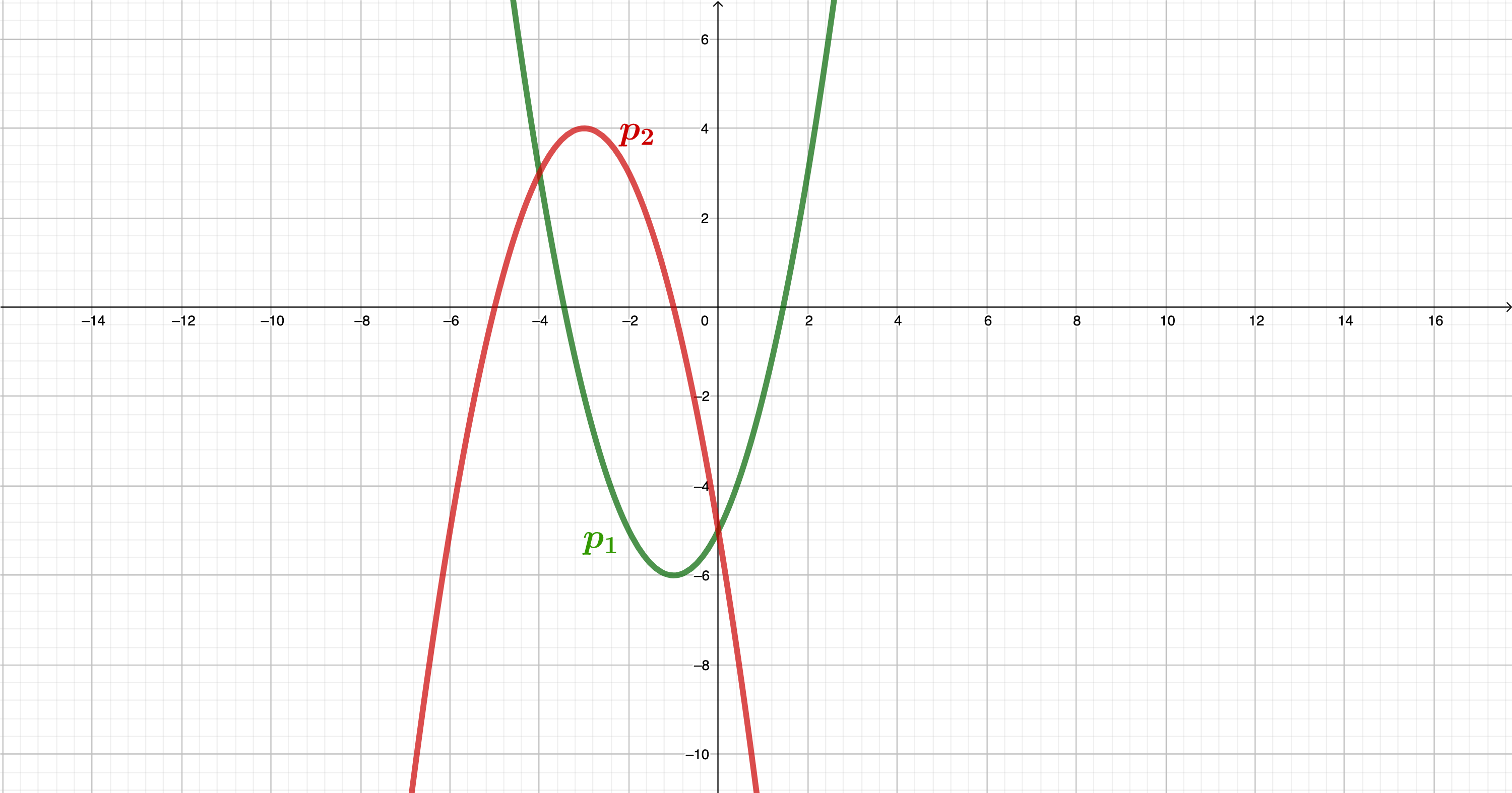
Die nach oben geöffnete Normalparabel hat den Scheitelpunkt
. Ermitteln Sie die Funktionsgleichung von in der Normalform.
Die Normalparabel hat die Funktionsgleichung : und schneidet die x-Achse in den Punkten und . Berechnen Sie die x-Koordinaten dieser Nullstellen.
Bestimmen Sie rechnerisch die Koordinaten des Scheitelpunkts der Normalparabel und geben Sie diesen an.
Zeichnen Sie die Parabeln und in ein Koordinatensystem mit der Längeneinheit 1 cm.
Eine nach oben geöffnete Normalparabel verläuft durch die Punkte und . Ermitteln Sie rechnerisch die Funktionsgleichung von in der Normalform.
Die Parabel hat die Funktionsgleichung : . Begründen Sie mithilfe einer Rechnung, dass die Parabel nach unten geöffnet ist.
- 6
Von einem Aussichtspunkt im Allgäu auf einer Höhe von 900 Meter über Normalnull (m ü. NN) aus betrachtet liegen die Gipfel der Berge Säuling und Zugspitze auf einer Geraden (siehe Skizze).
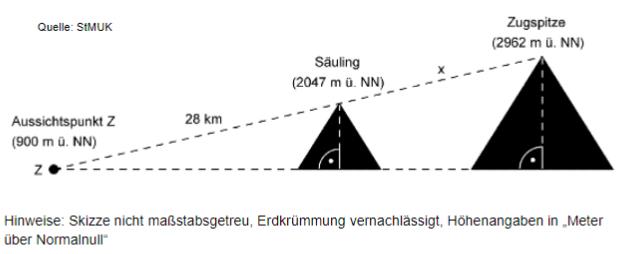
Berechnen Sie den Abstand x der beiden Gipfel voneinander, wenn die Entfernung vom Aussichtspunkt zum Gipfel des Säulings 28 km beträgt.
Die Höhe des „Säuling-Dreiecks“ könnte mit einer zentrischen Streckung auf die Höhe des „Zugspitze-Dreiecks“ abgebildet werden (Streckungszentrum Z ist der Aussichtspunkt). Ermitteln Sie den entsprechenden Streckungsfaktor k.
- 7
Bei einer Gleichung zur Anwendung einer binomischen Formel ist nur noch das gemischte (lineare) Glied bekannt. Stellen Sie eine mögliche vollständige Gleichung auf und notieren Sie diese auf Ihrem Lösungsblatt.
- 8
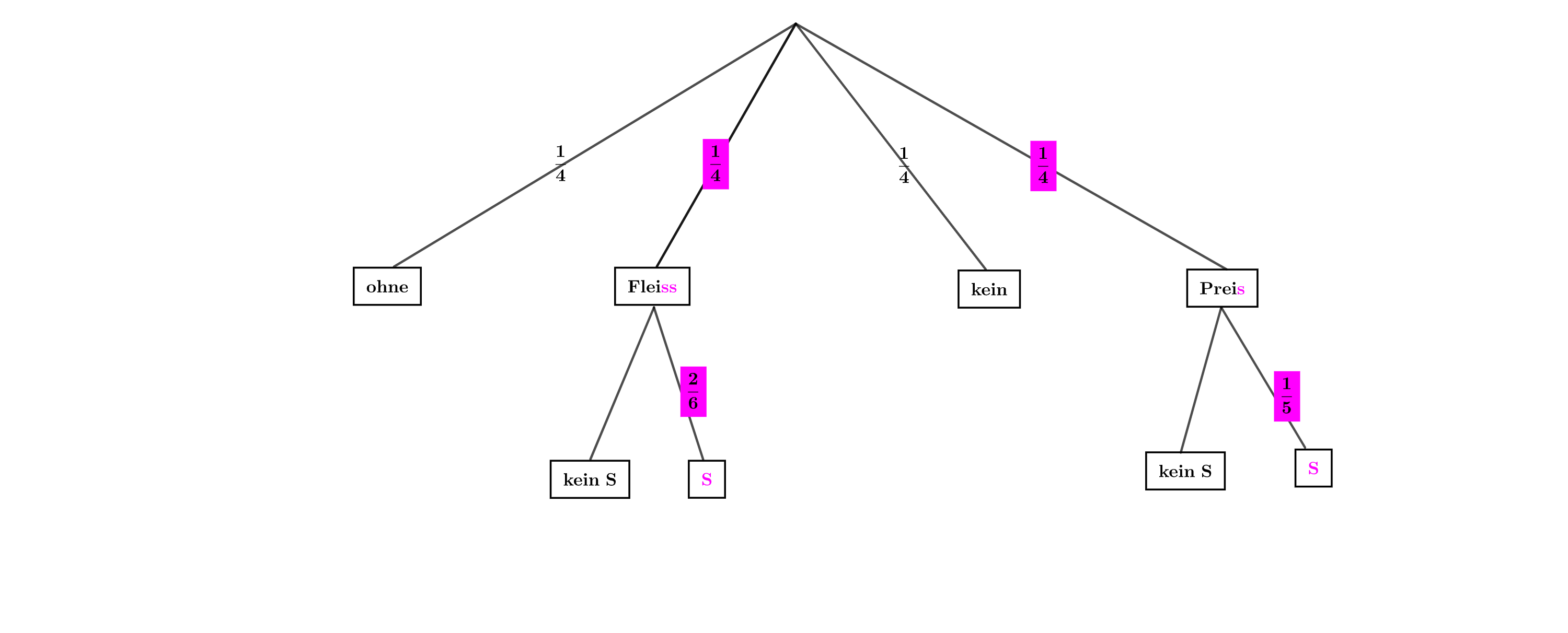
Sarah erstellt 19 Karten mit je einem Buchstaben, aus denen sich das folgende Sprichwort legen lässt:
OHNE FLEISS KEIN PREIS
Sie wirft alle Karten in eine Urne und zieht zufällig eine heraus. Berechnen Sie die Wahrscheinlichkeit, dass auf der Karte ein N steht.
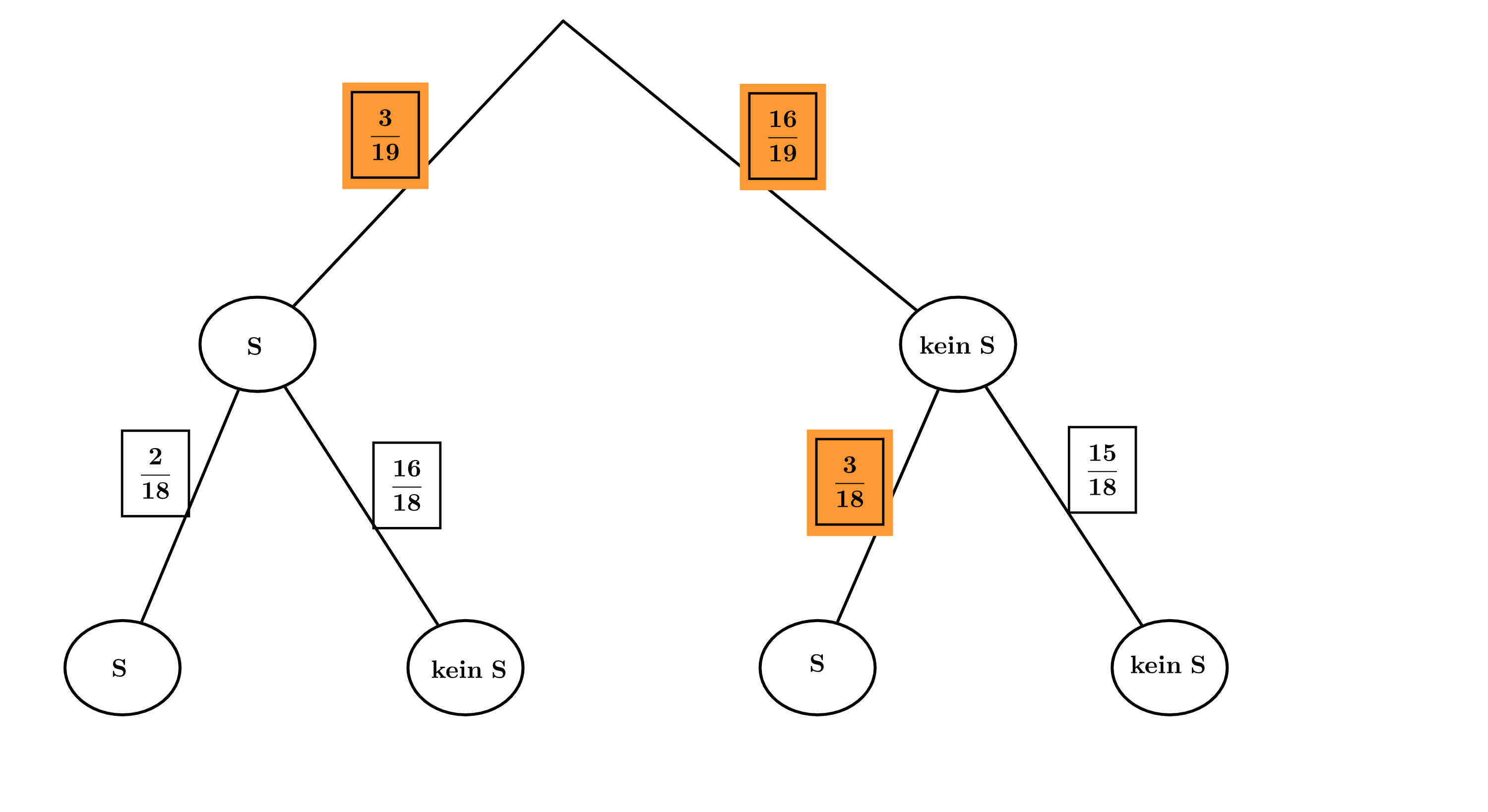
Sarah benutzt erneut eine Urne mit allen 19 Buchstabenkarten und zieht zweimal eine Karte ohne Zurücklegen. Sie unterscheidet nur zwischen den zwei Ereignissen „S“ und „kein S“. Erstellen Sie dazu ein Baumdiagramm, beschriften Sie die Äste mit den jeweiligen Wahrscheinlichkeiten und berechnen Sie, mit welcher Wahrscheinlichkeit Sarah mindestens ein S zieht.
Bei einem weiteren Zufallsexperiment verteilt Sarah die 19 Buchstabenkarten auf vier Urnen und gibt jedes Wort in eine eigene Urne. Sie wählt zufällig eine dieser Urnen aus und zieht daraus eine Karte. Ermitteln Sie rechnerisch die Wahrscheinlichkeit, mit der sie ein S zieht.
Aus der Urne mit den Buchstaben des Wortes PREIS zieht Sarah nacheinander alle Karten und legt sie in der gezogenen Reihenfolge auf den Tisch. Berechnen Sie die Anzahl aller möglichen verschiedenen Reihenfolgen der Buchstaben.
- 9
Vereinfachen Sie den folgenden Term so weit wie möglich. Es gilt: .
+
- 10
Eine Hohlkugel mit einem Außendurchmesser von 2 m soll als U-Boot verwendet werden. Diese Kugel besteht aus Metall und hat eine Wandstärke von 3,2 cm.
Die Kugel erhält außen einen Schutzanstrich. Berechnen Sie den zu streichenden Flächeninhalt.
Die Kugel wird zu Testzwecken mithilfe eines Krans in ein Becken gehoben. Ermitteln Sie rechnerisch die Masse in Tonnen, die der Kran mindestens heben muss, wenn Metall die Masse 7870 kg hat.
Das U-Boot soll in einem zylinderförmigen Tauchbecken mit einem Durchmesser von 3 m vollständig untergetaucht werden. Vor dem Eintauchen der Kugel beträgt der Wasserstand im Becken bereits 3 m. Berechnen Sie die Mindesthöhe des Tauchbeckens, damit das Wasser beim vollständigen Untertauchen des U-Boots nicht über den Beckenrand läuft.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?