Geometrie, Teil A, Aufgabengruppe 2

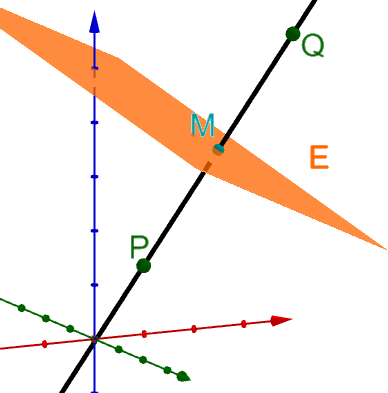
Wird der Punkt $P (1 | 2 | 3)$ an der Ebene $E$ gespiegelt, so ergibt sich der Punkt $Q (7 | 2 | 11)$ .

Bestimmen Sie eine Gleichung von $E$ in Koordinatenform. (3P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Ebene spiegeln
Der Vektor $\vec{P Q}$ ist ein Normalenvektor der gesuchten Ebene E.
Der Punkt $M$ ist die Mitte der Strecke $[P Q]$ und liegt in der Ebene $E$ .
Berechne den Vektor $\vec{P Q} = \vec{O Q} - \vec{O P}$ :
$\vec{P Q} = (\begin{array}{c} 7 \\ 2 \\ 11 \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) = (\begin{array}{c} 6 \\ 0 \\ 8 \end{array})$ $\Rightarrow \vec{n} = (\begin{array}{c} 6 \\ 0 \\ 8 \end{array})$
Berechne den Mittelpunkt der Strecke $[P Q]$ :
$\vec{O M} = \frac{1}{2} \cdot (\vec{O P} + \vec{O Q}) = \frac{1}{2} \cdot ((\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + (\begin{array}{c} 7 \\ 2 \\ 11 \end{array})) = (\begin{array}{c} 4 \\ 2 \\ 7 \end{array})$
Für die Ebene $E$ in Normalenform gilt allgemein:
$E : (\vec{O X} - \vec{O A}) \circ \vec{n} = 0$
Setze in $E$ für $\vec{O A}$ den Vektor $\vec{O M}$ und den Vektor $\vec{n}$ ein:
$E : (\vec{O X} - (\begin{array}{c} 4 \\ 2 \\ 7 \end{array})) \circ (\begin{array}{c} 6 \\ 0 \\ 8 \end{array}) = 0$
In Koordinatenform umgewandelt, folgt:
$E : 6 x_{1} + 8 x_{3} - (4 \cdot 6 + 2 \cdot 0 + 7 \cdot 8) = 0 $ $\Rightarrow E : 6 x_{1} + 8 x_{3} - 80 = 0$
Eine Gleichung von $E$ in Koordinatenform lautet: $E : 6 x_{1} + 8 x_{3} - 80 = 0$ .

Hast du eine Frage oder Feedback?
Kommentiere hier 👇
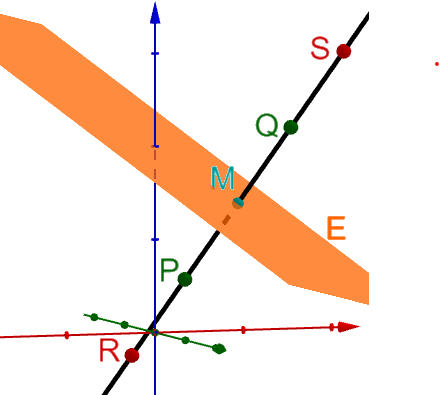
Auf der Geraden durch $P$ und $Q$ liegen die Punkte $R$ und $S$ symmetrisch bezüglich $E$ ; dabei liegt $R$ bezüglich $E$ auf der gleichen Seite wie $P$ . Der Abstand von $R$ und $S$ ist doppelt so groß wie der Abstand von $P$ und $Q$ . Bestimmen Sie die Koordinaten von $R$ . (2P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
$R$ liegt bezüglich $E$ auf der gleichen Seite wie $P$ (siehe Abbildung).
Es gilt: Der Abstand von $R$ und $S$ ist doppelt so groß wie der Abstand von $P$ und $Q$ . Demnach ist $[R S] = 2 \cdot [P Q]$ .
Der Punkt $M$ liegt in der Mitte der Strecke $[R S]$ , d.h. $[R M] = \frac{1}{2} [R S]$ .
$[R M] = \frac{1}{2} [R S] = \frac{1}{2} \cdot 2 \cdot [P Q] = [P Q]$
Vektoriell heißt die letzte Zeile: $\vec{R M} = \vec{P Q}$
$\vec{R M} = \vec{O M} - \vec{O R} = \vec{P Q}$ oder nach $\vec{O R}$ umgeformt:
$\vec{O R} = \vec{O M} - \vec{P Q} = (\begin{array}{c} 4 \\ 2 \\ 7 \end{array}) - (\begin{array}{c} 6 \\ 0 \\ 8 \end{array}) = (\begin{array}{c} - 2 \\ 2 \\ - 1 \end{array})$
Der Punkt $R$ hat die Koordinaten $R (- 2 | 2 | - 1)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?